深度解析:光学偏振器件的物理本源与前沿应用
摘要:偏振(Polarization)是横波区别于纵波的最根本特征,也是光作为电磁波矢量性质的直接体现。从17世纪惠更斯发现方解石的双折射现象,到现代量子光学中的光子自旋态操控,偏振器件始终是光学系统的“逻辑门”。本文将摒弃浅层的现象描述,从各向异性介质中的电动力学出发,推导各类偏振器件的物理机制,并探讨其在现代光子学中的极限应用。
1. 引言
光,作为电磁波,其本质由麦克斯韦方程组(Maxwell’s Equations)描述。在各向同性(Isotropic)的真空中,电场矢量 $\mathbf{E}$ 与磁场矢量 $\mathbf{B}$ 垂直于传播方向 $\mathbf{k}$,且在垂直平面内具有旋转对称性。然而,当我们引入“偏振”这一概念时,实际上是在讨论这种旋转对称性的破缺。
从自由度(Degree of Freedom)的角度来看,偏振赋予了光子除了频率、动量之外的额外信息载体——自旋角动量(Spin Angular Momentum, SAM)。理解偏振器件,本质上就是理解物质如何通过其微观结构(如晶格排列、分子取向)与光的电场矢量发生各向异性的相互作用。
2. 理论基石:麦克斯韦方程与琼斯矩阵
在进入具体器件分析前,我们必须建立数学描述体系。
2.1 平面波的矢量描述
对于沿 $z$ 轴传播的单色平面波,其电场矢量可表示为:
$$\mathbf{E}(z, t) = \begin{pmatrix} E_x \ E_y \end{pmatrix} e^{i(kz - \omega t)}$$
其中 $E_x$ 和 $E_y$ 是复振幅,包含振幅和相位信息。两者之间的相位差 $\delta = \phi_y - \phi_x$ 决定了偏振态:
- $\delta = 0$ 或 $\pi$:线偏振(Linear Polarization)。
- $\delta = \pm \pi/2$ 且 $|E_x| = |E_y|$:圆偏振(Circular Polarization)。
- 其他情况:椭圆偏振(Elliptical Polarization)。
2.2 琼斯矩阵(Jones Calculus)
为了定量描述器件对光的作用,我们引入琼斯向量和琼斯矩阵。一个光学系统 $J$ 对入射光 $\mathbf{E}_{in}$ 的变换为:
$$\mathbf{E}{out} = \mathbf{J} \cdot \mathbf{E}{in} = \begin{pmatrix} j_{xx} & j_{xy} \ j_{yx} & j_{yy} \end{pmatrix} \begin{pmatrix} E_{x} \ E_{y} \end{pmatrix}$$
这一线性代数工具将物理过程抽象为矩阵运算,是分析级联偏振系统的核心工具。
3. 吸收型偏振器:电子的阻尼振荡
最基础的偏振控制是只允许特定方向的电场通过,阻挡与之垂直的分量。这通常通过二向色性(Dichroism) 实现。
3.1 金属线栅偏振器(Wire Grid Polarizer, WGP):亚波长光学的胜利
金属线栅偏振器不仅仅是微波屏蔽效应的简单延伸,它是亚波长光学(Sub-wavelength Optics)与超材料(Metamaterials) 概念的早期雏形。其核心在于通过人工结构的几何各向异性,在宏观上合成出天然材料难以具备的极端双折射特性。
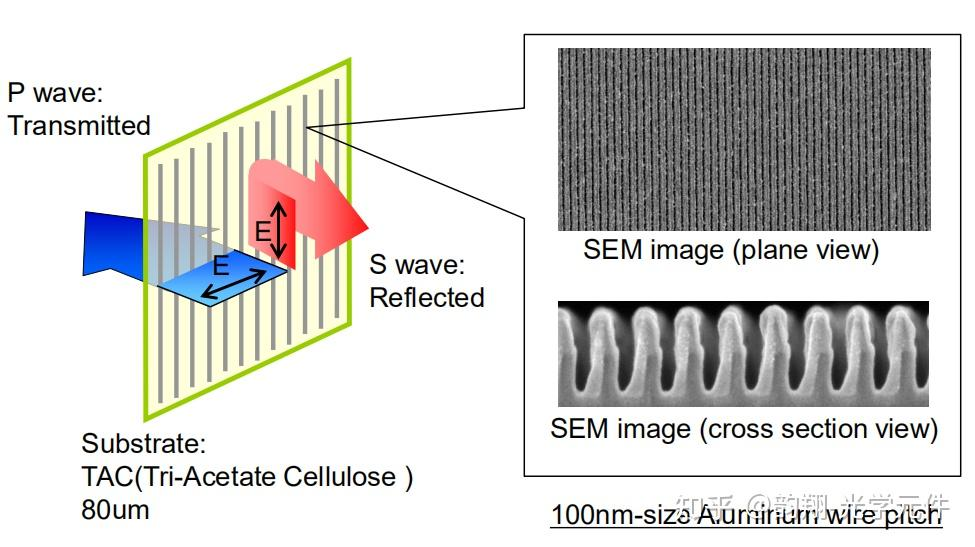
3.1.1 微观动力学:自由电子与受限电子的博弈
要理解WGP,必须从金属中电子的微观运动出发。假设入射光波长为 $\lambda$,金属光栅的周期为 $p$,且满足 $p \ll \lambda$(通常要求 $p < \lambda/3$ 甚至更小)。此时,光波无法“分辨”出单根导线,而是感受到一种平均化的各向异性介质。
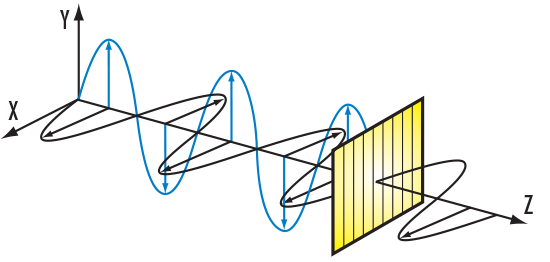
平行偏振态(TE Polarization, $\mathbf{E} \parallel \text{wires}$):自由振荡与反向辐射
当电场矢量平行于金属线方向时,金属内的自由电子受到洛伦兹力驱动。由于导线在纵向上是连续的,电子的平均自由程(Mean Free Path)远小于导线长度,电子可以像在体金属(Bulk Metal)中一样进行长距离的自由振荡。
根据经典电动力学,这些振荡的电子流构成了表面电流 $\mathbf{J}$。这个感应电流会辐射出一个与入射场相位相反、振幅几乎相等的电磁波(由于金属的高电导率)。- 向前传播方向:辐射波与入射波发生相消干涉(Destructive Interference),导致透射光强几乎为零。
- 向后传播方向:辐射波形成反射波。
结论:对于平行光,WGP表现为一面金属镜。
垂直偏振态(TM Polarization, $\mathbf{E} \perp \text{wires}$):退极化场与介质化
当电场矢量垂直于金属线时,电子试图跟随电场运动,但立即撞击到纳米线的边界。由于导线宽度极窄(通常仅几十纳米),电子在边界处堆积,形成了一个强大的静电场——退极化场(Depolarization Field)。
这个由边界电荷产生的退极化场 $\mathbf{E}{dep}$ 方向与外加电场 $\mathbf{E}{ext}$ 相反,极大地抵消了驱动力。电子被“锁定”在极小的区域内无法自由流动。
此时,电子的运动不再表现为宏观电流,而是类似于电介质中的偶极子振荡。金属不再像金属,而更像是一种低折射率的电介质。
结论:对于垂直光,WGP表现为透明介质。
3.1.2 数学模型:有效介质理论(EMT)
为了定量描述这种各向异性,我们可以使用零阶有效介质理论。假设光栅由金属(填充因子 $f$,介电常数 $\epsilon_m$)和空气/基底间隙(介电常数 $\epsilon_d$)组成。
由于 $\epsilon_m$ 在可见光及红外波段通常是复数且实部为大的负值(如 $\epsilon_{Ag} \approx -16 + 0.5i$ @ 600nm),这导致了极端的各向异性:
对于平行分量(Ordinary Permittivity):
介电常数遵循算术平均:
$$\epsilon_{\parallel} = f \epsilon_m + (1-f) \epsilon_d$$
由于 $\epsilon_m$ 的实部是巨大的负数,导致 $\epsilon_{\parallel}$ 也是大的负数。根据折射率 $n = \sqrt{\epsilon}$,$\epsilon_{\parallel} < 0$ 意味着折射率是纯虚数,光波在介质中是指前衰减的(Evanescent),表现为强反射和吸收。对于垂直分量(Extraordinary Permittivity):
介电常数遵循谐波平均(类似于串联电容):
$$\frac{1}{\epsilon_{\perp}} = \frac{f}{\epsilon_m} + \frac{1-f}{\epsilon_d}$$
$$\Rightarrow \epsilon_{\perp} = \frac{\epsilon_m \epsilon_d}{f \epsilon_d + (1-f) \epsilon_m}$$
有趣的是,当 $|\epsilon_m| \gg \epsilon_d$ 时(良导体条件),分母中的 $(1-f)\epsilon_m$ 主导,式子近似为 $\epsilon_{\perp} \approx \epsilon_d / (1-f)$。
这是一个正实数!意味着 $\epsilon_{\perp}$ 代表一种透明的、折射率略高于空气的介质,光波可以低损耗透过。
3.1.3 工程挑战与现代应用
传统的WGP受限于光刻精度,长期局限于红外波段。但随着纳米压印(Nanoimprint Lithography) 和电子束曝光(EBL) 技术的发展,现代可见光WGP的周期已达到 100nm-150nm 量级。
相比传统棱镜的优势:
- 平面化与紧凑性:厚度仅为微米级,易于集成到像元级偏振相机(On-chip Polarization Sensor)中。
- 大视场角(AOI):与依赖全反射角的格兰棱镜不同,WGP在宽入射角下仍能保持较好的消光比。
- 耐热性:全无机结构(铝/玻璃)使其能承受投影仪光源产生的高温,而聚合物偏振片会烧毁。
局限性:
瑞利共振(Rayleigh Resonance):当入射波长 $\lambda$ 接近光栅周期 $p$ 时(即不再满足 $p \ll \lambda$),EMT理论失效,光栅进入衍射区,透过率和消光比会发生剧烈波动。因此,制造工艺的极限直接决定了WGP的最短工作波长。
3.2 聚合物偏振片(Polaroid)
由 Edwin Land 发明的偏振片利用了拉伸的聚乙烯醇(PVA)链吸附碘分子的结构。碘链形成了导电的长链分子。其物理机制与金属线栅完全一致:沿长链方向的导电性导致该方向电场分量被吸收(转化为焦耳热),而垂直方向透射。
4. 双折射器件:晶格的各向异性
吸收型偏振器虽然廉价,但抗损伤阈值低且存在吸收损耗。高能激光和精密光学更倾向于使用基于双折射(Birefringence) 的晶体器件。
4.1 双折射的微观起源
在各向异性晶体(如方解石、YVO4、α-BBO)中,晶格结构的非对称性导致电子在不同方向上的“弹簧系数”(恢复力常数)不同。这意味着介电常数 $\epsilon$ 不再是一个标量,而是一个二阶张量 $\boldsymbol{\epsilon}$。
根据 $\mathbf{D} = \boldsymbol{\epsilon} \mathbf{E}$,电位移矢量 $\mathbf{D}$ 与电场 $\mathbf{E}$ 方向通常不重合。这导致光在晶体中传播时,存在两个特征折射率:
- o光(Ordinary ray):遵循折射定律,折射率为 $n_o$。
- e光(Extraordinary ray):不遵循标准折射定律,折射率随角度变化,介于 $n_o$ 和 $n_e$ 之间。
4.2 格兰-泰勒棱镜(Glan-Taylor Prism)
作为高功率激光系统中的“黄金标准”,格兰-泰勒棱镜以其极高的消光比(Extinction Ratio, 通常可达 $10^5:1$ 甚至 $10^6:1$)和卓越的抗损伤阈值而著称。
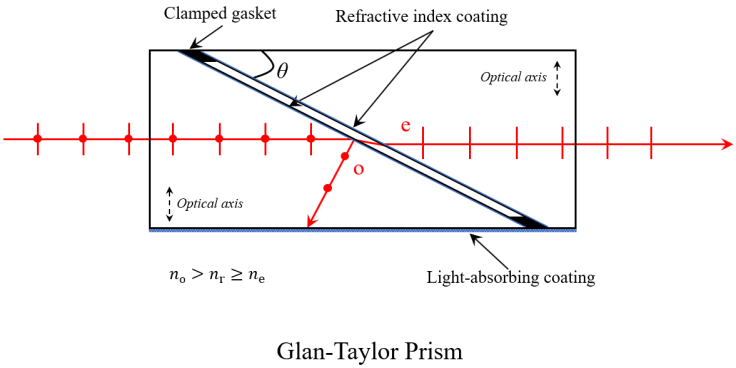
图:格兰-泰勒棱镜的光路示意图,注意中间的空气隙(Air Gap)
几何结构与材料:
该器件由两个直角方解石棱镜组成,并未像普通透镜那样胶合在一起,而是通过精密机械装配保持微小的空气隙(Air Gap)。棱镜的切割角度经过精确计算,光轴通常垂直于传播方向(如图中 $\updownarrow$ 所示)。物理原理:全反射(TIR)的选择性过滤
其核心机制在于利用双折射晶体中 o光 和 e光 巨大的折射率差异,构建一个只允许一种光通过的“全反射陷阱”。
假设光束入射到中间的方解石/空气界面。对于波长 590nm 的光,方解石的折射率为:
$$n_o \approx 1.658, \quad n_e \approx 1.486$$
由于空气的折射率 $n_{air} \approx 1.0$,根据全反射公式 $\theta_c = \arcsin(n_{air}/n_{crystal})$,我们可以计算出两个临界角:- o光临界角:$\theta_{c,o} = \arcsin(1/1.658) \approx 37.0^\circ$
- e光临界角:$\theta_{c,e} = \arcsin(1/1.486) \approx 42.3^\circ$
工作窗口:通过切割棱镜,使内部光线在空气隙界面的入射角 $\theta$ 落在两者之间(例如设计为 $39^\circ$):
$$\theta_{c,o} < \theta < \theta_{c,e}$$
在此条件下:- o光(垂直于光轴):满足全反射条件($\theta > \theta_{c,o}$),在界面处发生 100% 全反射,随后被棱镜侧面的黑色吸光涂层吸收或导出。
- e光(平行于光轴):不满足全反射条件($\theta < \theta_{c,e}$),顺利透过空气隙进入第二个棱镜。
工程设计亮点:
- 空气隙 vs. 胶合层:这是它与格兰-汤普森(Glan-Thompson)棱镜的最大区别。胶合棱镜使用的光学胶在高能激光(如脉冲激光)照射下会吸收能量导致发热、变黑甚至燃烧。空气隙结构消除了这一弱点,使其能承受极高的激光功率密度(> $500 \text{ MW/cm}^2$)。
- 布儒斯特角优化:为了减少 e光 在空气隙界面的反射损耗(菲涅尔反射),棱镜的切割角通常接近 e光 的布儒斯特角(Brewster Angle)。这使得 e光 能够以接近 100% 的透过率穿过空气层,保证了极高的透过效率。
局限性:
由于全反射的角宽限制($\Delta \theta = \theta_{c,e} - \theta_{c,o}$ 仅有约 $5^\circ$),格兰-泰勒棱镜的**视场角(Field of View)**相对较窄,且具有非对称性。入射光必须准直较好,否则边缘光线会因角度偏差而无法正确分离。
4.3 沃拉斯顿棱镜(Wollaston Prism)
沃拉斯顿棱镜是一种极其经典的偏振分束器,它利用双折射材料的折射率突变,将非偏振光高效率地分离为两束振动方向互相垂直的线偏振光。与格兰棱镜不同,它保留了两束光,且两束光呈对称的偏折角出射。
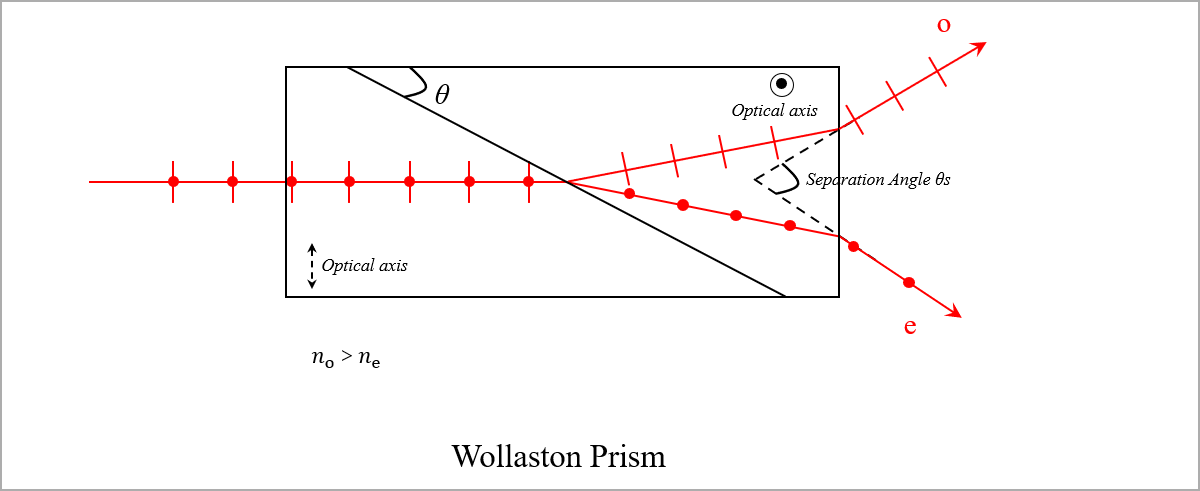
图:沃拉斯顿棱镜的光路示意图(以方解石 $n_o > n_e$ 为例)
几何结构:
由两个直角楔形棱镜(通常为方解石或石英)胶合而成。关键在于光轴的排布:- 前棱镜:光轴与入射面平行(图中为竖直方向)。
- 后棱镜:光轴也与入射面平行,但与前棱镜的光轴旋转了 90°(图中为垂直纸面方向)。
物理机制:相对论性的“身份互换”
沃拉斯顿棱镜的工作原理本质上是一场关于参照系的变换游戏。光在穿越两块晶体的界面时,其偏振方向保持不变,但相对于晶体晶格的“身份”发生了翻转。入射阶段(无分离):
光垂直入射第一块晶体。此时,垂直偏振分量($\perp$ 光轴)被定义为 o光(折射率 $n_o$),水平偏振分量($\parallel$ 光轴)被定义为 e光(折射率 $n_e$)。由于是垂直入射,根据斯涅尔定律,两者传播方向未发生改变,只是相速度不同。界面突变(关键步骤):
当光束到达胶合界面进入第二块晶体时,晶体的光轴旋转了 90°。- 原 o光(垂直偏振):现在的振动方向与新光轴平行,因此瞬间“变身”为 e光。其感受到的折射率从 $n_o$ 突变为 $n_e$。
- 原 e光(水平偏振):现在的振动方向与新光轴垂直,因此瞬间“变身”为 o光。其感受到的折射率从 $n_e$ 突变为 $n_o$。
双向折射分离:
根据斯涅尔定律,折射率的改变导致光线在倾斜界面处发生偏折(以方解石 $n_o > n_e$ 为例):- 光束 1 ($n_o \to n_e$):从光密介质进入光疏介质,光速加快,折射光线远离法线偏折。
- 光束 2 ($n_e \to n_o$):从光疏介质进入光密介质,光速减慢,折射光线靠近法线偏折。
结果与应用:
这种相反的折射行为使得两束正交偏振光以大致对称的角度分开。其分离角 $\theta_s$ 可近似表示为:
$$\theta_s \approx 2 |n_e - n_o| \tan \alpha$$
其中 $\alpha$ 为楔角。这种器件常用于微分干涉差显微镜(DIC)以及偏振成像系统中。
5. 相位延迟器件:波片(Waveplates)
波片不改变光的强度,只改变正交偏振分量之间的相位差。
5.1 物理机制
当线偏振光射入双折射晶体(如石英、云母),且偏振方向与晶体光轴成一定角度(通常45°)时,光分解为快轴(Fast Axis,折射率小)和慢轴(Slow Axis, 折射率大)分量。
5.1.1 矢量分解与折射率差异
假设一块单轴晶体(如石英),其光轴平行于表面。我们在晶体平面上定义两个正交的主轴:
- 快轴(Fast Axis, $n_f$):折射率较小,光在该方向传播速度快($v_f = c/n_f$)。
- 慢轴(Slow Axis, $n_s$):折射率较大,光在该方向传播速度慢($v_s = c/n_s$)。
当一束线偏振光垂直入射,且其偏振方向与快轴夹角为 $\theta$ 时,入射电场 $\mathbf{E}{in}$ 被强制投影到这两个轴上:
$$\mathbf{E}{in} = E_0 \cos\theta \cdot \hat{\mathbf{e}}_f + E_0 \sin\theta \cdot \hat{\mathbf{e}}_s$$
这就是关键所在:晶体并不直接传输原始的偏振矢量,而是分别独立地传输这两个分量。
5.1.2 相位差(Retardation)的积累推导
两个分量在晶体中独立传播。由于相速度不同,它们在穿过厚度为 $d$ 的晶体时,积累的光程(Optical Path Length, OPL)也不同:
- 快轴分量光程:$L_f = n_f d$
- 慢轴分量光程:$L_s = n_s d$
两者的光程差为 $\Delta L = (n_s - n_f) d$。
为了将光程差转化为相位差 $\Gamma$(即慢轴分量比快轴分量“滞后”了多少相位),我们将光程差乘以真空波数 $k_0 = 2\pi/\lambda$:
$$\Gamma = k_0 \Delta L = \frac{2\pi}{\lambda} (n_s - n_f) d$$
5.1.3 为什么通常选择 45°?
公式中的 $\theta$ 决定了两个分量的振幅比例。
- 若 $\theta = 0^\circ$ 或 $90^\circ$:光只沿着一个轴传播,$\Gamma$ 失去意义,偏振态不改变。
- 若 $\theta = 45^\circ$:此时 $\cos(45^\circ) = \sin(45^\circ) = 1/\sqrt{2}$。快轴和慢轴分量获得相等的振幅。这是实现从线偏振到圆偏振转换(对于 $\lambda/4$ 波片)的必要条件。如果振幅不等,合成的将是椭圆偏振而非圆偏振。
最终,出射光 $\mathbf{E}{out}$ 是这两个带有新相位关系的矢量之和:
$$\mathbf{E}{out} \propto \hat{\mathbf{e}}_f + e^{i\Gamma} \hat{\mathbf{e}}_s$$
正是这一项 $e^{i\Gamma}$,决定了出射光是线偏振、圆偏振还是椭圆偏振。
5.2 常见类型
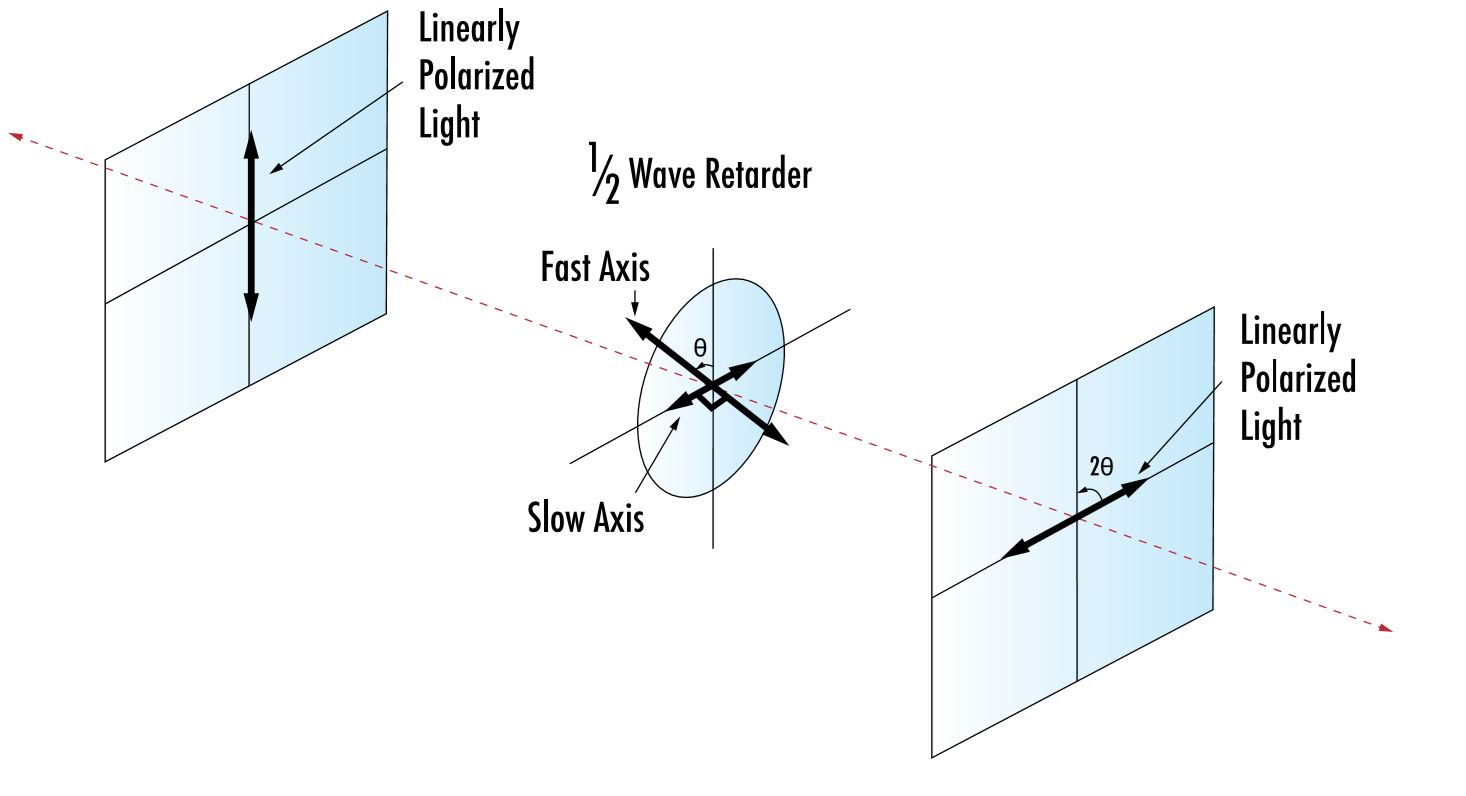
- 半波片(Half-Wave Plate, HWP):
- $\Gamma = \pi$。
- 功能:旋转线偏振光的方向。若入射偏振方向与快轴夹角为 $\theta$,出射光偏振方向转过 $2\theta$。
- 琼斯矩阵(快轴沿水平方向):
$$\mathbf{J}_{\lambda/2} = \begin{pmatrix} -i & 0 \ 0 & i \end{pmatrix} = e^{-i\pi/2} \begin{pmatrix} 1 & 0 \ 0 & -1 \end{pmatrix}$$
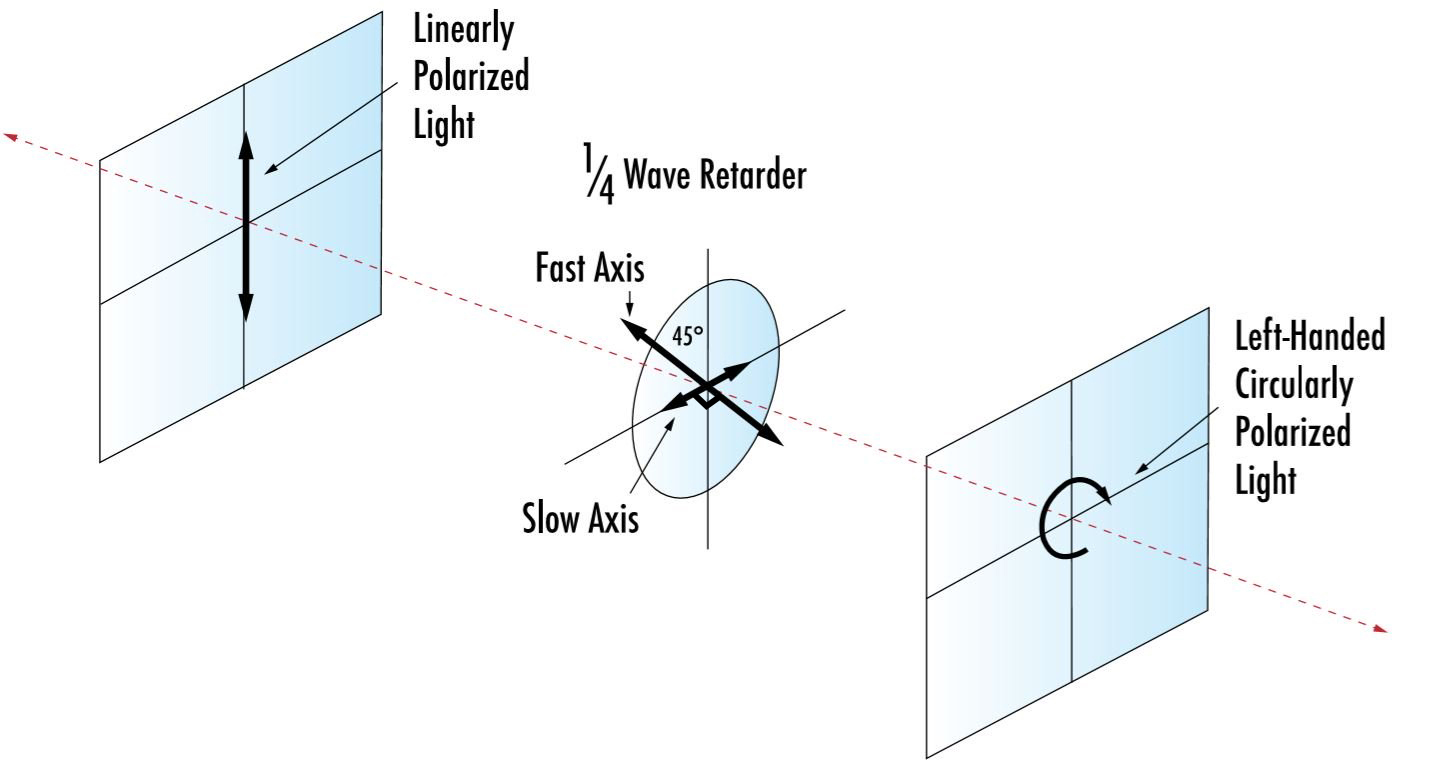
- 四分之一波片(Quarter-Wave Plate, QWP):
- $\Gamma = \pi/2$。
- 功能:实现线偏振与圆/椭圆偏振的互转。
- 琼斯矩阵:
$$\mathbf{J}_{\lambda/4} = e^{-i\pi/4} \begin{pmatrix} 1 & 0 \ 0 & i \end{pmatrix}$$
5.3 零级波片 vs. 多级波片
- 多级波片:实际相位差为 $2m\pi + \Gamma$。厚度大,易加工,但对波长和温度极其敏感(色散严重)。
- 零级波片:实际相位差即为 $\Gamma$。通常由两块光轴正交、厚度微差的波片胶合而成(Compound Zero-Order)。带宽宽,稳定性高,是高精度实验的首选。
Edmund上面有个写的比较好的波片原理的解释,感兴趣的可以去这里看在
了解波片和延迟器
6. 旋光器件与非互易性:法拉第隔离器
前述器件多基于线性双折射,具有互易性(光路可逆)。而在光通信和激光系统中,我们常需要“光二极管”——光隔离器。
6.1 法拉第效应(Faraday Effect)
这是一种磁致旋光效应。当线偏振光通过施加了纵向磁场 $\mathbf{B}$ 的介质时,其偏振面会发生旋转。旋转角 $\beta$ 为:
$$\beta = V B L$$
其中 $V$ 是费尔德常数(Verdet Constant),$L$ 是介质长度。
核心特征:非互易性。无论光是正向传播还是反向传播,偏振旋转的方向是相对于磁场定义的,而不是相对于波矢量。这意味着光往返一次,旋转角会累加($2\beta$),而不是抵消。
6.2 光隔离器的工作原理
一个标准的光隔离器包含三个部分:
- 输入偏振器(起偏器,如垂直方向)。
- 法拉第旋光器(设计为旋转 45°)。
- 输出偏振器(检偏器,方向为 45°)。
- 正向:垂直偏振光 $\to$ 旋转 45° $\to$ 通过输出偏振器。
- 反向:45° 反向光进入旋光器 $\to$ 再次沿同一方向旋转 45°(变成 90°,即水平方向) $\to$ 遇到垂直方向的输入偏振器 $\to$ 被阻断。
这在保护高功率激光器免受回光损伤中起着至关重要的作用。
7. 前沿应用案例分析
7.1 量子计算与量子密钥分发(QKD)
在BB84协议中,信息的编码依赖于光子的偏振态(如水平/垂直作为一组基,+45°/-45°作为另一组基)。
- 电光调制器(EOM):利用普克尔斯效应(Pockels Effect),通过电压快速改变晶体的双折射率,从而在纳秒量级动态调制光子的偏振态(量子比特)。这里对波片的相位延迟精度要求极高,通常需要主动温度控制。
7.2 偏振复用光通信(PDM-QPSK)
现代相干光通信利用光的偏振正交性,在同一光纤中传输两路独立信号(PDM,Polarization Division Multiplexing),使容量翻倍。
- **偏振分束器(PBS)**在此处作为相干接收机的前端,将混合信号分离。随后的数字信号处理(DSP)算法会补偿光纤中的偏振模色散(PMD)。
7.3 超表面(Metasurfaces)偏振器件
传统器件受限于材料厚度和体积。基于亚波长微纳结构的超表面,可以通过设计各向异性的“超原子”(Meta-atoms),在亚波长尺度上对光的偏振、相位和振幅进行任意调控。
- 应用:超薄平面透镜、全息显示、矢量光束产生(如径向偏振光、角向偏振光)。
8. 结论与展望
从巴塞林纳斯(Bartholinus)发现冰洲石的双折射至今,偏振光学已经从单纯的现象观察发展为现代光子学的基石。
理解偏振器件,不仅是掌握格兰棱镜或波片的使用,更是理解光作为矢量波与物质微观结构相互作用的深层物理。
随着纳米加工技术的发展,未来的偏振器件将不再局限于块状晶体,而是向集成化、薄膜化、动态可调化方向演进。超表面与液晶技术的结合,甚至允许我们在像素级别动态重构光的偏振态,这将彻底改变显示技术、全息成像以及光子神经网络的面貌。