光影的双重奏：双折射的物理本源、精密调控与工程挑战

“光在晶体中的传播，不再是单一路径的简单旅行，而是由物质微观结构的对称性破缺所指挥的一场精密分裂。”

在光学领域，很少有现象能像双折射（Birefringence） 那样，既具有令人着迷的视觉美感，又蕴含着如此深刻的物理真理。它是经典光学的基石，也是现代光子学、量子通信和精密测量的核心机制。

一、 双折射原理：微观各向异性与介电张量

要理解双折射，我们必须回到光与物质相互作用的根本。光是一种电磁波，当光穿过介质时，其振荡的电场（$\mathbf{E}$）会扰动介质中的电子云，诱导产生电偶极矩。这种极化效应由电位移矢量（$\mathbf{D}$）描述。

1.1 从标量到张量：对称性的破缺

在各向同性介质（如真空、玻璃）中，电子受到的恢复力在各个方向上是相同的。诱导出的极化强度 $\mathbf{P}$ 与电场 $\mathbf{E}$ 平行，电位移矢量与电场的关系是简单的标量关系：$\mathbf{D} = \epsilon \mathbf{E}$。

然而，在各向异性晶体（如方解石、石英）中，晶格结构在不同方向上的原子排列密度和键合力不同。这就好比电子被弹簧束缚在原子核周围，但这些“弹簧”在x、y、z方向上的劲度系数（stiffness）不同。

当电场 $\mathbf{E}$ 施加时，电子云的位移（即极化方向）不再必然与电场方向平行。此时，介电常数必须升级为一个二阶张量（Tensor）：

$$\mathbf{D} = \bar{\bar{\epsilon}} \mathbf{E}$$

展开矩阵形式为：

$$
\begin{pmatrix} D_x \ D_y \ D_z \end{pmatrix} =
\epsilon_0 \begin{pmatrix}
\epsilon_{xx} & \epsilon_{xy} & \epsilon_{xz} \
\epsilon_{yx} & \epsilon_{yy} & \epsilon_{yz} \
\epsilon_{zx} & \epsilon_{zy} & \epsilon_{zz}
\end{pmatrix}
\begin{pmatrix} E_x \ E_y \ E_z \end{pmatrix}
$$

通过选择合适的主轴坐标系（Principal Axes），我们可以将该张量对角化，消去非对角项。此时，三个主轴方向对应的介电常数为 $\epsilon_x, \epsilon_y, \epsilon_z$。

1.2 折射率椭球（The Index Ellipsoid）

定义主折射率为 $n_i = \sqrt{\epsilon_i/\epsilon_0}$，这构成了著名的菲涅耳折射率椭球方程：

$$\frac{x^2}{n_x^2} + \frac{y^2}{n_y^2} + \frac{z^2}{n_z^2} = 1$$

这个几何模型是理解双折射的核心。当光波沿某一方向 $\mathbf{k}$ 传播时，我们需要通过椭球中心做一个垂直于 $\mathbf{k}$ 的切面。该切面通常是一个椭圆，这个椭圆的长轴和短轴分别代表了该传播方向上两个允许的正交偏振态（本征态）的折射率。

1.3 晶体结构与双折射分类：对称性的决定论

介电张量的形式并非随机，它受到晶体点群对称性的严格约束（Neumann 原理）。根据晶胞参数（$a, b, c$）和晶轴夹角（$\alpha, \beta, \gamma$）的对称性，自然界的7大晶系被严格划分为三类光学介质：

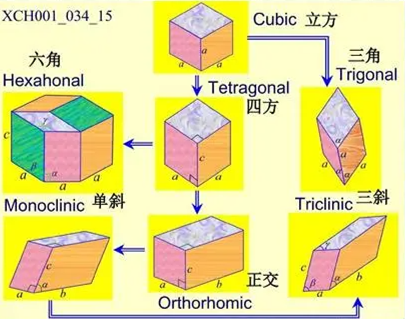
A. 各向同性介质（Isotropic）：

• 对应晶系： 立方晶系（Cubic System）。
• 物理机制： 由于晶胞高度对称（$a=b=c, \alpha=\beta=\gamma=90^\circ$），电子在 $x, y, z$ 三个方向受到的束缚力完全相同。
• 张量特征： 介电张量的对角元相等：$\epsilon_x = \epsilon_y = \epsilon_z$。
• 结果： 折射率椭球退化为一个球体（Sphere）。光在任何方向传播速度都相同，不存在双折射。
• 典型材料： 钻石（Diamond）、氯化钠（NaCl）、砷化镓（GaAs）。

B. 单轴晶体（Uniaxial Crystals）：

• 对应晶系： 六方（Hexagonal）、四方（Tetragonal）、三方（Trigonal）。
• 物理机制： 这些晶体在一个主轴（通常是 c 轴）上具有旋转对称性，但在垂直于该轴的平面内是各向同性的。
• 张量特征： $\epsilon_x = \epsilon_y \neq \epsilon_z$。
  • 光轴（Optic Axis）： 唯一的特殊方向（z轴），沿此方向传播不发生双折射。
  • 分类：
    • 正单轴（Positive）： $n_e > n_o$ （如石英，$n_z > n_x$）。光轴方向折射率大，光速慢。
    • 负单轴（Negative）： $n_e < n_o$ （如方解石，$n_z < n_x$）。光轴方向折射率小，光速快。
• 典型材料： 方解石（Calcite）、石英（Quartz）、蓝宝石（Sapphire）。

C. 双轴晶体（Biaxial Crystals）：

• 对应晶系： 正交（Orthorhombic）、单斜（Monoclinic）、三斜（Triclinic）。
• 物理机制： 晶胞对称性极低，三个基矢长度不等且/或夹角不垂直。电子在三个正交方向上的束缚力均不相同。
• 张量特征： $\epsilon_x \neq \epsilon_y \neq \epsilon_z$。
• 结果： 折射率椭球是三轴不等的椭球。存在两个特殊的方向（光轴），沿这两个方向传播时折射率相等，不发生双折射。这两个光轴的夹角称为光轴角（$2V$）。
• 典型材料： 云母（Mica）、黄玉（Topaz）、橄榄石（Olivine）。

工程启示： 在设计需要高度偏振敏感的光学系统（如波片）时，我们通常首选单轴晶体，因为其物理模型更简单，光轴容易定位。而双轴晶体虽然双折射特性更丰富，但其复杂的相位延迟特性往往给精密加工带来挑战。

二、 寻常光与非寻常光：物理定义与数学区分

在单轴晶体（如方解石、石英）中，存在一个特殊的旋转对称轴，称为光轴（Optic Axis, c-axis）。此时 $n_x = n_y = n_o$，$n_z = n_e$。光束进入晶体后会分裂为两束性质截然不同的光：寻常光（o-ray）和非寻常光（e-ray）。

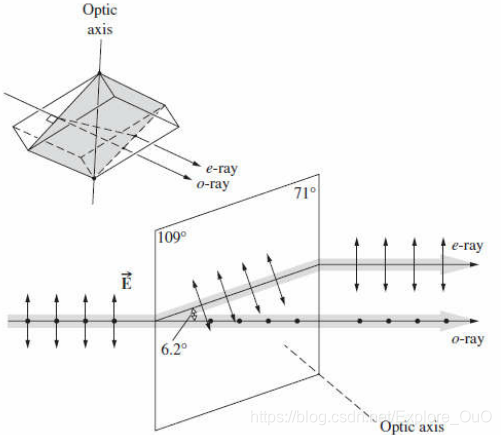
2.1 寻常光（Ordinary ray, o-光）

• 定义：其电位移矢量 $\mathbf{D}_o$ 垂直于由光轴和波矢量 $\mathbf{k}$ 构成的“主平面”（Principal Plane）。
• 物理特性：无论光向哪个方向传播，o-光的电场矢量始终只感受到 $n_o$。
• 传播规律：波面为球面，严格遵守斯涅尔折射定律（Snell’s Law），折射光线始终在入射面内。

2.2 非寻常光（Extraordinary ray, e-光）

• 定义：其电位移矢量 $\mathbf{D}_e$ 位于主平面内。这意味着它与光轴有一定的夹角。
• 物理特性：e-光感受到的有效折射率 $n_{eff}(\theta)$ 是传播方向角 $\theta$（$\mathbf{k}$ 与光轴的夹角）的函数。
• 数学公式（核心公式）：
  $$\frac{1}{n_{eff}^2(\theta)} = \frac{\cos^2\theta}{n_o^2} + \frac{\sin^2\theta}{n_e^2}$$
  • 当 $\theta = 0^\circ$（沿光轴传播）：$n_{eff} = n_o$，不发生双折射。
  • 当 $\theta = 90^\circ$（垂直光轴传播）：$n_{eff} = n_e$，双折射最强。

2.3 惠更斯作图法下的双折射传播机制

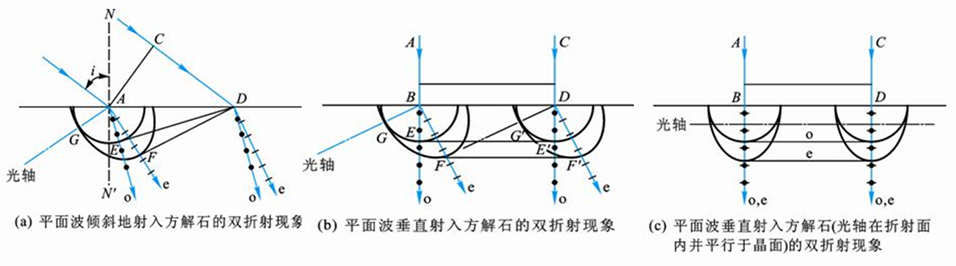
图解：惠更斯作图法下的双折射传播机制

该图利用惠更斯原理展示了平面波进入负单轴晶体（方解石，$n_e < n_o$，即 $v_e > v_o$）时的波前演化。图中半圆代表 o 光波面，半椭圆代表 e 光波面。

• 图 (a) 平面波倾斜入射：双折射分离

  • 现象： 光束倾斜入射。o 光遵循斯涅尔定律，折射光线在入射面内。e 光由于在晶体内的波面是旋转椭球，其折射方向与其波面切点连线（光线方向）不再垂直于波前。
  • 结果： 这一过程导致 o 光和 e 光的折射角不同，两束光在空间上分离开来。

• 图 (b) 平面波垂直入射（光轴倾斜）：非常光(e光)的特殊偏折

  • 修正点： 在此图中，光垂直入射界面。o 光波面是球面，波法线与光线重合，直接穿过不偏折。e 光虽然波前（包络面 $CD$）仍平行于界面，但由于光轴倾斜，椭圆波面是倾斜的。
  • 关键机制： e 光的光线方向定义为从波源点到波面与包络线切点的连线（图中 $B$ 到 $E$，或 $D$ 到 $E’$）。
  • 结论： 尽管入射角为 0 度，e 光的光线方向（能流方向）却发生了偏折，这就是离散效应（Walk-off）。e 光不再沿直线传播，而是向一侧“滑移”。

• 图 (c) 平面波垂直入射（光轴在表面内且平行于入射面）：速度差异

  • 修正点： 此处光轴平行于晶体表面。对于负晶体（方解石），e 光是快光，o 光是慢光。
  • 现象： o 光波面（圆）和 e 光波面（椭圆）的中心都在法线上。因此，o 光和 e 光的光线方向均不发生偏折，沿直线传播。
  • 关键差异： 请注意图中椭圆的长轴（e 光）明显长于圆的半径（o 光）。这意味着在相同时间内，e 光传播的距离更远。
  • 物理意义： 虽然两束光路径重合，但传播速度不同 ($v_e > v_o$)。这导致两束光在穿过晶体后产生相位差，这正是波片（Waveplate） 改变偏振态的原理。

三、 波片技术：相位调控的工程实现

波片（Retarder）利用双折射率 $\Delta n = n_e - n_o$ 在两个正交偏振分量间引入相位延迟（Retardance）。在工程上，如何做到“准确控制”是区分高端与低端光学的关键。

基本的相位延迟公式为：
$$\Gamma = \frac{2\pi}{\lambda} |n_e - n_o| d$$
其中 $d$ 为晶体厚度。

3.1 多级波片（Multi-order Waveplate）：廉价但脆弱

• 原理：直接使用较厚（如 0.5mm）的晶体片。其产生的总相位延迟为：
  $$\Gamma_{total} = 2m\pi + \Gamma_{target}$$
  其中 $m$ 是整数（通常 $m \approx 10 \sim 100$）。
• 问题：极不稳定。
  • 温度敏感性：由于 $m$ 很大，折射率随温度的微小变化（热光系数 $dn/dT$）或厚度的热膨胀，都会被放大 $m$ 倍，导致相位严重漂移。
  • 波长敏感性：带宽极窄，激光波长稍微漂移，相位差就会偏离 $\lambda/4$ 或 $\lambda/2$。

3.2 零级波片（Zero-order Waveplate）：高精度的标杆

为了准确控制相位，必须消除 $m$，使 $m=0$。

• 真零级（True Zero-order）：

  • 实现：将晶体抛光到极薄（例如石英需抛光到约 15 $\mu m$），直接满足 $\Gamma = \lambda/2$。
  • 优劣：性能极其优越，带宽宽，对温度不敏感。但机械强度极差，易碎，加工极其困难。

• 复合零级（Compound Zero-order / Air-spaced）：

  • 实现：使用两片厚度分别为 $d_1$ 和 $d_2$ 的晶体，将它们的光轴互相垂直（交叉 90度） 胶合或空气间隔放置。
  • 原理：光先经过快轴，再经过慢轴，相位差相互抵消。净相位差由厚度差决定：
    $$\Gamma \propto |n_e - n_o| (d_1 - d_2)$$
  • 优势：我们可以让 $d_1 \approx d_2$（例如 0.500mm 和 0.515mm），从而在获得宏观机械强度的同时，实现零级的光学性能。这是高精度实验室的标准配置。

四、 常见材料双折射参数对比表

选择正确的材料是光学设计的起点。以下是常用晶体在 $\lambda = 589 \text{nm}$ 处的关键参数：

材料名称	化学式	晶体类型	$n_o$	$n_e$	$\Delta n$ (双折射率)	典型应用与评价
方解石	CaCO$_3$	负单轴	1.658	1.486	-0.172	极高双折射。用于格兰-泰勒棱镜（Glan-Taylor），能在大角度下分离光束。质地较软，易吸潮。
金红石	TiO$_2$	正单轴	2.616	2.903	+0.287	超高双折射。常用于光纤通信的光隔离器和环行器中，用于紧凑空间内的光束分离。
石英	SiO$_2$	正单轴	1.544	1.553	+0.009	低双折射。性能极其稳定，透过率高，硬度高。是制作高精度波片的首选材料。
铌酸锂	LiNbO$_3$	负单轴	2.286	2.200	-0.086	高电光系数。主要用于电光调制器、Q开关。通过施加电压可改变其折射率。
蓝宝石	Al$_2$O$_3$	负单轴	1.768	1.760	-0.008	极硬/耐高温。常用作保护窗口。虽然双折射率低，但在高分辨率成像中仍需注意其带来的像散。
YVO4	YVO$_4$	正单轴	1.958	2.168	+0.210	高双折射。方解石的替代品，硬度更好，易于加工，常用于光纤器件中的分束器。

注：正单轴($n_e > n_o$)光轴为慢轴；负单轴($n_e < n_o$)光轴为快轴。