电磁波的矢量灵魂:从偏振原理到 TE/TM 模的深度物理剖析
1. 引言
在初等光学的学习中,我们往往关注光的强度(Intensity)、频率(Frequency)和相位(Phase),却容易忽视光的第四个核心属性——偏振(Polarization)。
偏振是电磁波作为矢量波(Vector Wave) 的直接体现。如果说频率决定了光的颜色,相位决定了干涉条纹的位置,那么偏振则描述了电磁场在空间中舞动的“姿态”。从液晶显示屏(LCD)的显像原理,到量子密钥分发中的光子自旋态,偏振无处不在。
本文将从偏振的原理出发,对TE和TM偏振的区别给出详细解释。
2. 理论基石:麦克斯韦方程组与横波本质
2.1 波动方程
一切电磁现象的起点皆为麦克斯韦方程组。在无源($\rho=0, \mathbf{J}=0$)、线性、各向同性的均匀介质中,麦克斯韦方程组形式如下:
(1) 高斯定律:$\nabla \cdot \mathbf{E} = 0$
(2) 高斯磁定律:$\nabla \cdot \mathbf{B} = 0$
(3) 法拉第定律:$\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$
(4) 安培-麦克斯韦定律:$\nabla \times \mathbf{B} = \mu\epsilon \frac{\partial \mathbf{E}}{\partial t}$
为了探究波的传播特性,我们对式 (3) 取旋度,并利用矢量恒等式 $\nabla \times (\nabla \times \mathbf{A}) = \nabla(\nabla \cdot \mathbf{A}) - \nabla^2 \mathbf{A}$ 以及式 (1),得到电场的矢量波动方程:
$$ \nabla^2 \mathbf{E} - \mu\epsilon \frac{\partial^2 \mathbf{E}}{\partial t^2} = 0 $$
对于沿 $z$ 轴传播的平面单色波,其解具有如下形式:
$$ \mathbf{E}(\mathbf{r}, t) = \mathbf{E}_0 e^{i(kz - \omega t)} $$
2.2 为什么光是横波?
将上述解代入高斯定律 $\nabla \cdot \mathbf{E} = 0$,我们可以得到:
$$ \nabla \cdot \mathbf{E} = \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} + \frac{\partial E_z}{\partial z} = i k E_z = 0 $$
由于 $k \neq 0$,必然导出 $E_z = 0$。这表明电场矢量 $\mathbf{E}$ 必须垂直于传播方向 $\mathbf{k}$(即 $z$ 轴方向)。这一数学约束从根本上定义了电磁波的横波(Transverse Wave) 性质,也正是偏振现象存在的物理前提——只有横波才有偏振,纵波(如声波)无所谓偏振方向。
3. 偏振态的演化与数学描述
由于 $\mathbf{E}$ 被限制在 $xy$ 平面内,我们可以将其分解为两个正交分量。这两个分量的振幅比和相对相位差决定了具体的偏振态。
设电场矢量为:
$$ \mathbf{E}(z,t) = \hat{x} E_{0x} e^{i(kz - \omega t)} + \hat{y} E_{0y} e^{i(kz - \omega t + \delta)} $$
其中 $\delta = \phi_y - \phi_x$ 是两个分量间的相位差。
3.1 线偏振 (Linear Polarization)
当相位差 $\delta = m\pi$ ($m=0, \pm 1, \pm 2…$) 时,两个分量同相或反相振动。此时合成矢量在 $xy$ 平面上的轨迹是一条直线。
$$ \frac{E_y}{E_x} = (-1)^m \frac{E_{0y}}{E_{0x}} = \text{Constant} $$
这是最简单的偏振态,也是大多数激光器的输出模式。
3.2 圆偏振 (Circular Polarization)
当满足两个严格条件:
- 振幅相等:$E_{0x} = E_{0y} = E_0$
- 相位差为 $\pi/2$ 的奇数倍:$\delta = \pm \pi/2$
此时,电场矢量的大小保持不变 $|\mathbf{E}| = E_0$,但方向随时间以角频率 $\omega$ 旋转。
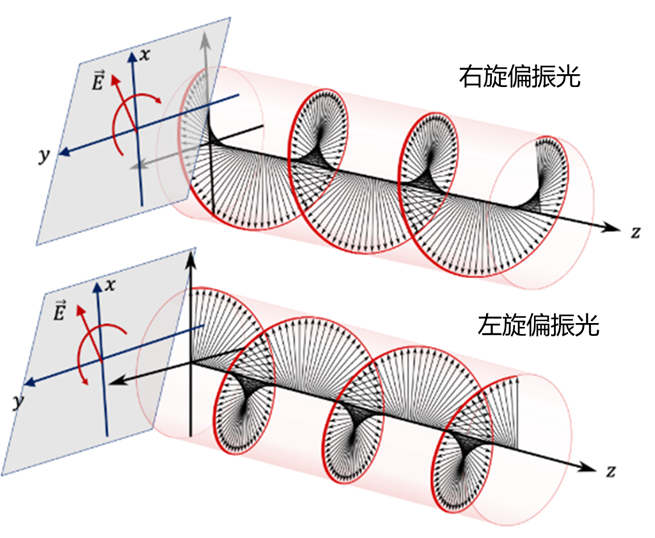
- 右旋圆偏振 (RCP):通常定义为面向波源观察,电场顺时针旋转。
- 左旋圆偏振 (LCP):电场逆时针旋转。
在复数域中,圆偏振可以优雅地表示为基矢量 $\hat{x} \pm i\hat{y}$。
3.3 椭圆偏振 (Elliptical Polarization)
这是偏振的最一般形态。当振幅不等或相位差不是 $\pi/2$ 的整数倍时,电场矢量的端点轨迹是一个椭圆。从数学上讲,线偏振和圆偏振只是椭圆偏振的退化特例。
3.4 琼斯矢量 (Jones Vector)
为了在计算中更方便地处理偏振,物理学引入了琼斯矢量 $\mathbf{J}$。对于沿 $z$ 轴传播的波,去掉时空因子,仅保留振幅和相位信息:
$$ \mathbf{J} = \begin{pmatrix} E_{0x} \ E_{0y} e^{i\delta} \end{pmatrix} $$
- 水平线偏振:$\begin{pmatrix} 1 \ 0 \end{pmatrix}$
- 右旋圆偏振:$\frac{1}{\sqrt{2}} \begin{pmatrix} 1 \ -i \end{pmatrix}$
琼斯微积分(Jones Calculus)通过矩阵运算,极大地简化了光通过偏振片、波片等器件的计算过程。
更多有关琼斯矢量的描述,可以查看另一片文章琼斯矩阵与偏振变换
4. TE 模与 TM 模
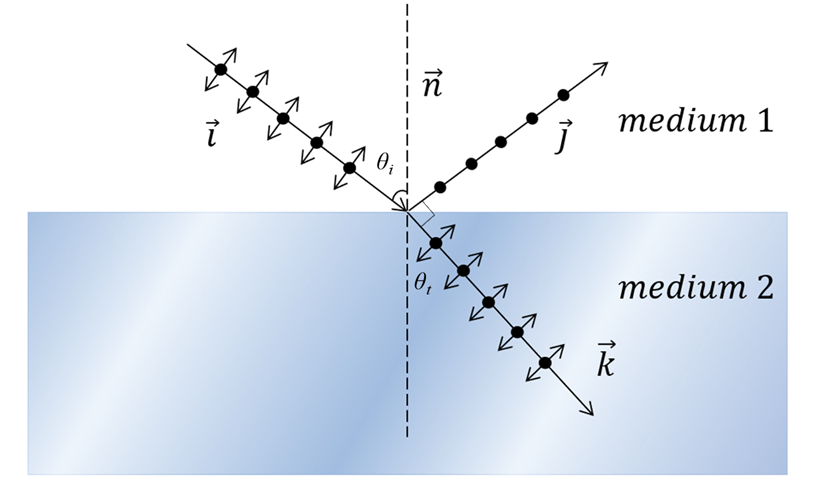
当电磁波从一种介质入射到另一种介质的界面时,简单的 $x, y$ 分解不再适用。我们需要根据入射面(Plane of Incidence)——由入射波矢 $\mathbf{k}_i$ 和界面法线 $\mathbf{n}$ 构成的平面——来重新定义坐标系。
这就是 TE(Transverse Electric) 和 TM(Transverse Magnetic) 模式登场的时刻。
4.1 几何基准:定义“入射面” (The Plane of Incidence)
在讨论界面光学时,我们首先必须建立一个局部坐标系。对于任何投射到界面上的光波,都存在一个唯一的参考平面,称为入射面。
- 定义:由入射波的波矢 $\mathbf{k}_i$(传播方向)与界面法线 $\mathbf{n}$ 共同确定的平面。
- 物理意义:它是破坏空间旋转对称性的基准。有了入射面,我们才能定义什么是“平行”,什么是“垂直”。
4.2 TE 模式 / s-偏振
TE 和 s-偏振 描述的是同一种物理状态,只是命名视角不同。
1. TE (Transverse Electric,横电模)
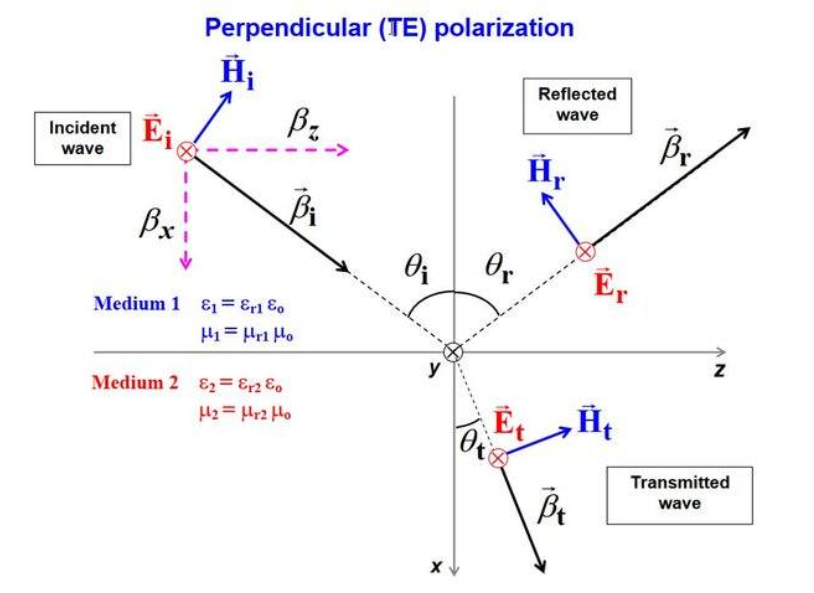
- 物理定义:电场矢量 $\mathbf{E}$ 或偏振方向完全垂直于入射面。
- 矢量特征:由于电场垂直于入射面,而入射面包含法线,这意味着电场矢量 $\mathbf{E}$ 必定平行于介质的分界面。
- 磁场方向:根据右手定则($\mathbf{E} \times \mathbf{H} \parallel \mathbf{k}$),若电场垂直于入射面,则磁场矢量 $\mathbf{H}$ 必然位于入射面内。
2. s-偏振 (s-polarization)
- 词源:源自德语单词 “senkrecht”,意为“垂直的”。
4.3 TM 模式 / p-偏振
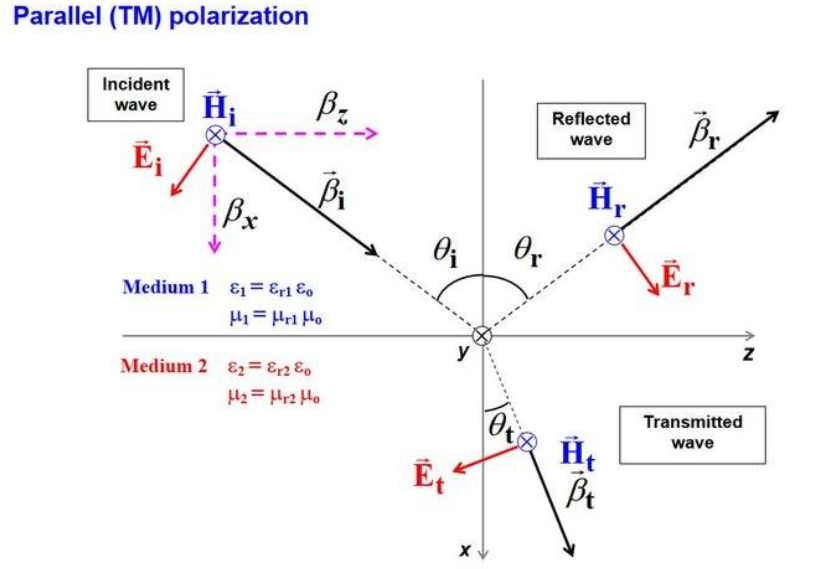
TM 和 p-偏振 对应另一种正交状态。
1. TM (Transverse Magnetic,横磁模)
- 物理定义:磁场矢量 $\mathbf{H}$ 完全垂直于入射面。
- 矢量特征:由于电磁波的正交性,如果磁场垂直于入射面,那么电场矢量 $\mathbf{E}$ 或偏振方向必然位于入射面内。
- 关键推论:因为 $\mathbf{E}$ 在入射面内,它不再单纯平行于界面。$\mathbf{E}$ 矢量可以分解为两个分量:一个垂直于界面($E_{\perp}$),一个平行于界面($E_{\parallel}$)。正是这个垂直于界面的电场分量,使得 TM 波能够驱动表面电荷,从而激发表面等离激元(SPP)或产生布儒斯特角效应。
2. p-偏振 (p-polarization)
- 词源:源自德语单词 “parallel”,意为“平行的”。
- 含义:电场矢量 $\mathbf{E}$ 与入射面平行。
4.4 总结对比表
| 特性维度 | TE / s-偏振 | TM / p-偏振 |
|---|---|---|
| 全称 | Transverse Electric / senkrecht | Transverse Magnetic / parallel |
| 电场 $\mathbf{E}$ | 垂直于入射面 (平行于界面) | 平行于入射面 (躺在平面内) |
| 磁场 $\mathbf{H}$ | 平行于入射面 | 垂直于入射面 |
| 几何直觉 | $\mathbf{E}$ 刺破纸面 (Dots/Crosses) | $\mathbf{E}$ 在纸面内画箭头 (Arrows) |
| 物理后果 | 在界面处无垂直电场分量,无法激发 SPP | 存在垂直电场分量,可激发表面波 |
| 反射特性 | 反射率随角度单调增加 | 存在布儒斯特角 (反射率为0) |
4.5 实际案例1:菲涅耳方程 (Fresnel Equations) 的差异
利用电磁场边界条件($\mathbf{E}$ 的切向分量连续,$\mathbf{H}$ 的切向分量连续),我们可以推导出反射系数 $r$ 和透射系数 $t$。这里展示反射系数的差异,这是理解两者行为不同的关键:
TE 模反射系数 $r_s$:
$$ r_s = \frac{n_1 \cos \theta_i - n_2 \cos \theta_t}{n_1 \cos \theta_i + n_2 \cos \theta_t} $$
TM 模反射系数 $r_p$:
$$ r_p = \frac{n_2 \cos \theta_i - n_1 \cos \theta_t}{n_2 \cos \theta_i + n_1 \cos \theta_t} $$
4.6 实际案例2:布儒斯特角 (Brewster’s Angle) 的物理本质
仔细观察上述公式,你会发现一个惊人的差异:
- 对于 TE 模,只要 $n_1 \neq n_2$,分子 $n_1 \cos \theta_i - n_2 \cos \theta_t$ 永远不会为零(除了掠射角)。也就是说,TE 光总是会被反射。
- 对于 TM 模,存在一个特定的角度 $\theta_B$,使得分子为零,即 $r_p = 0$。这就是布儒斯特角。
$$ \tan \theta_B = \frac{n_2}{n_1} $$
5. 波导中的 TE 与 TM:被束缚的光
在光纤或金属波导中,光不再是自由传播的平面波,而是被限制在有限空间内的本征模(Eigenmodes)。这里的 TE 和 TM 有了更严格的定义。
5.1 矩形波导分析
在传播方向为 $z$ 的波导中:
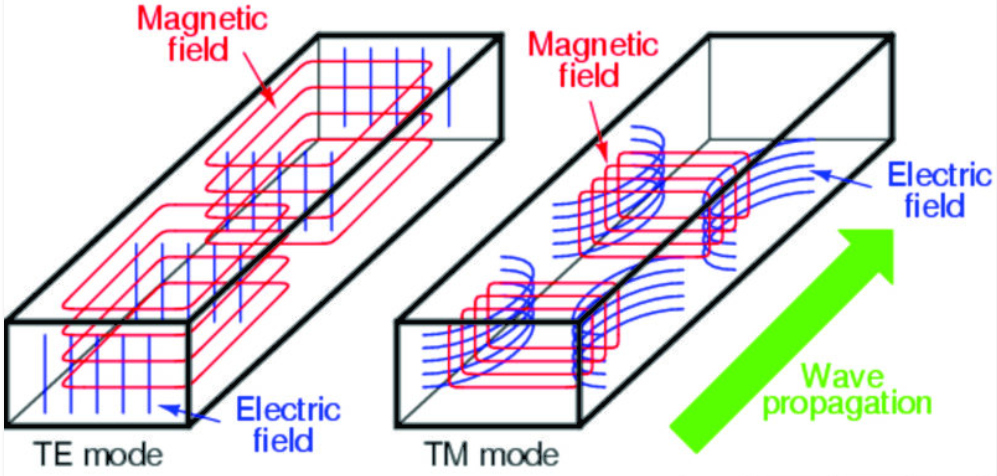
- TE 模:$E_z = 0$。纵向没有电场分量,只有磁场分量 $H_z$。
- TM 模:$H_z = 0$。纵向没有磁场分量,只有电场分量 $E_z$。
求解亥姆霍兹方程并应用金属边界条件($E_{tangential} = 0$),我们会发现不同的模式对应不同的截止频率(Cutoff Frequency):
$$ f_{c, mn} = \frac{1}{2\sqrt{\mu\epsilon}} \sqrt{\left(\frac{m}{a}\right)^2 + \left(\frac{n}{b}\right)^2} $$
有趣的是,对于矩形波导,最低阶模式通常是 $TE_{10}$ 模。
5.2 TE偏振和TE模式有什么区别?
在偏振光学与波导光学中,TE 和 TM 这两个术语经常让人困惑。关键在于理解:虽然物理根源相同,但定义的参照系完全不同。
界面光学 (Polarization):参照物是入射面 (Plane of Incidence)。
- TE (s-pol):电场 $\mathbf{E}$ 垂直于入射面。
- TM (p-pol):磁场 $\mathbf{H}$ 垂直于入射面。
- 这里的“Transverse”指的是横截于入射面。
波导理论 (Modes):参照物是传播轴 (Propagation Axis, $z$-axis)。
- TE 模:传播方向上无电场分量 ($E_z = 0$)。
- TM 模:传播方向上无磁场分量 ($H_z = 0$)。
- 这里的“Transverse”指的是横截于波的宏观传播方向。
核心差异总结表
| 比较维度 | 界面偏振 (Interface Polarization) | 波导模式 (Waveguide Modes) |
|---|---|---|
| 定义基准 | 相对于入射面 | 相对于传播轴 ($z$) |
| 纵向分量 | 视为局部平面波,通常忽略 | 关键特征:TM 模必有 $E_z$,TE 模必有 $H_z$ |
| TEM 模 | 自由空间光波皆为 TEM | 矩形波导不存在 TEM 模,仅存在于多导体系统(如同轴线) |
| 存在条件 | 任何频率、任何角度皆可分解 | 只有满足截止频率 ($f > f_c$) 的离散本征态才能存在 |
| 能量流向 | 沿 $\mathbf{k}$ 矢量方向 | 沿 $z$ 轴螺旋前进 (群速度 < 光速) |
一句话总结:波导里的 TE/TM 模,就是界面上的 TE/TM 偏振光被“困”在两面墙之间来回反弹的宏观表现。
5.2 TEM 模的特殊性
有一种特殊的模式叫 TEM(Transverse Electromagnetic),即 $E_z = 0$ 且 $H_z = 0$。
根据数学推导,TEM 模只能存在于多导体系统(如同轴电缆)中。在单导体空心波导中,TEM 模无法存在。这是由拉普拉斯方程在单连通域内的唯一性定理决定的:如果边界电势为常数,内部电势必为常数,导致电场为零。
6. 总结与工程启示
通过对 TE 和 TM 的深入对比,我们可以得出具有极高工程价值的结论:
| 特性 | TE 模 (s-pol) | TM 模 (p-pol) |
|---|---|---|
| 电场方向 | 垂直入射面 | 平行入射面 |
| 布儒斯特角 | 不存在 (总有反射) | 存在 (反射可为零) |
| 表面等离激元 (SPP) | 无法激发 | 可以激发 (利用 $E_z$ 分量) |
| 波导截止频率 | 通常较低 (如 $TE_{10}$) | 通常较高 |
| 相位跃变 | 全反射时相位移动不同 | 全反射时相位移动不同 |
工程应用场景:
- 摄影滤镜:利用布儒斯特角原理,偏振镜可以滤除水面或玻璃面的反射光(这些反射光主要是 TE 分量,透射的是 TM 分量,滤镜阻挡 TE 即可)。
- 激光器窗口:激光管的窗口通常被切成布儒斯特角,以使得 TM 模无损通过,从而强制激光器输出纯线偏振光。
- 生物传感:表面等离激元共振(SPR)传感器必须使用 TM 光激发,因为只有 TM 光具备垂直于金属表面的电场分量,能引起表面电荷密度的波动。