感知的量化：色彩度量学原理与不均匀性（Mura）计算的数学基础

色彩，本质上并非物质的固有属性，而是一种 心理物理学（Psychophysics） 现象。它是光波（物理输入）与人类视觉系统（生理接收）相互作用后，在大脑皮层产生的感知（心理输出）。

对于工程师和科学家而言，主观的“红”或“蓝”是无法用于制造标准化的。我们需要一把尺子，将这种主观感知映射到客观的向量空间中。本文将从麦克斯韦电磁理论出发，推导色彩量化的数学模型，并最终解决一个实际工程问题：如何计算一个平面上的色彩不均匀性（Color Non-uniformity）。

---

第一部分：从光子到神经信号（物理与生理基础）

要量化色彩，首先必须量化光。光是电磁波，其物理特性由 光谱功率分布（Spectral Power Distribution, SPD） 描述。

1.1 光谱功率分布 $S(\lambda)$

任意光源的物理属性可以由一个函数 $S(\lambda)$ 表示，其中 $\lambda$ 是波长（单位通常为nm），$S$ 是该波长下的辐射功率（单位 $W/m^2/nm$）。可见光范围通常定义为 380nm 到 780nm。

1.2 人眼的线性积分器模型：从无限维到三维的坍缩

人类对色彩的感知始于视网膜上的光感受器。根据杨-赫姆霍兹（Young-Helmholtz）的三色视学说，正常人眼视网膜上镶嵌着三种类型的视锥细胞（Cones）。尽管在通俗语境中常被称为“红、绿、蓝”感光细胞，但在学术上，根据其光谱响应峰值的位置，更严谨地将其命名为 长波（L-Cones, ~560nm）、中波（M-Cones, ~530nm） 和 短波（S-Cones, ~420nm） 受体。

从信号处理的第一性原理来看，人眼本质上是一个低通滤波后的线性积分器。物理世界中的光，其光谱功率分布（SPD）$S(\lambda)$ 是一个定义在连续波长域上的函数，理论上属于无限维的希尔伯特空间（Hilbert Space）。然而，视觉系统通过积分运算，将这个无限维的物理信息强行“投影”到了一个三维的欧几里得空间中。

设三种视锥细胞的光谱灵敏度函数分别为 $l(\lambda), m(\lambda), s(\lambda)$，则物理光谱转化为神经刺激值 $(L, M, S)$ 的过程如下：

$$
\begin{align}
L &= \int_{\lambda_{min}}^{\lambda_{max}} S(\lambda) l(\lambda) d\lambda \
M &= \int_{\lambda_{min}}^{\lambda_{max}} S(\lambda) m(\lambda) d\lambda \
S &= \int_{\lambda_{min}}^{\lambda_{max}} S(\lambda) s(\lambda) d\lambda
\end{align}
$$

这个积分过程揭示了一个深刻的数学事实：这是一场巨大的信息丢失（Lossy Compression）。我们将拥有无数自由度的光谱曲线 $S(\lambda)$ 压缩成了仅有三个自由度的向量。

正因为这种维度的剧烈坍缩（从 $\infty$ 到 3），导致了色彩科学中最核心、也是最神奇的现象——同色异谱（Metamerism）。这是一个典型的线性代数中的“多对一映射”（Many-to-One Mapping）问题。

由于我们只有三个积分约束方程，却有无数种可能的 $S(\lambda)$ 函数形状，数学上必然存在无穷多组完全不同的光谱分布 $S_1(\lambda)$ 和 $S_2(\lambda)$，使得它们在上述积分运算后得到完全相同的 $(L, M, S)$ 向量：

$$
\int S_1(\lambda) \mathbf{c}(\lambda) d\lambda = \int S_2(\lambda) \mathbf{c}(\lambda) d\lambda \quad (\text{其中 } \mathbf{c} \in {l, m, s})
$$

这意味着，对于人眼而言，只要最终的三刺激值相等，物理上截然不同的光就是“同一种颜色”。这是现代显示技术的物理基石：我们不需要在屏幕像素中重建真实太阳的连续光谱来显示“黄色”，我们只需要混合适当比例的红光（R）和绿光（G），就能构造出一个在积分结果上等效的刺激向量，从而欺骗大脑产生完全一致的色彩感知。

---

第二部分：CIE 1931 XYZ——构建标准观察者

LMS空间虽然生理上正确，但由于缺乏标准化且存在负值（在颜色匹配实验中出现），CIE（国际照明委员会）在1931年引入了线性变换，构建了CIE XYZ 色彩空间。

2.1 颜色匹配函数（Color Matching Functions）

CIE 定义了三个标准的颜色匹配函数 $\bar{x}(\lambda), \bar{y}(\lambda), \bar{z}(\lambda)$。其中 $\bar{y}(\lambda)$ 被特意设计为与人眼的明视觉光谱光视效率函数 $V(\lambda)$ 一致，代表亮度感知。

三刺激值（Tristimulus Values） $X, Y, Z$ 的计算公式为：

$$
X = k \int_{380}^{780} S(\lambda) \bar{x}(\lambda) d\lambda
$$

$$
Y = k \int_{380}^{780} S(\lambda) \bar{y}(\lambda) d\lambda
$$

$$
Z = k \int_{380}^{780} S(\lambda) \bar{z}(\lambda) d\lambda
$$

其中 $k$ 是归一化常数。对于物体色，通常取 $k = 100 / \int S_{ref}(\lambda)\bar{y}(\lambda)d\lambda$，其中 $S_{ref}$ 是参考光源的光谱。

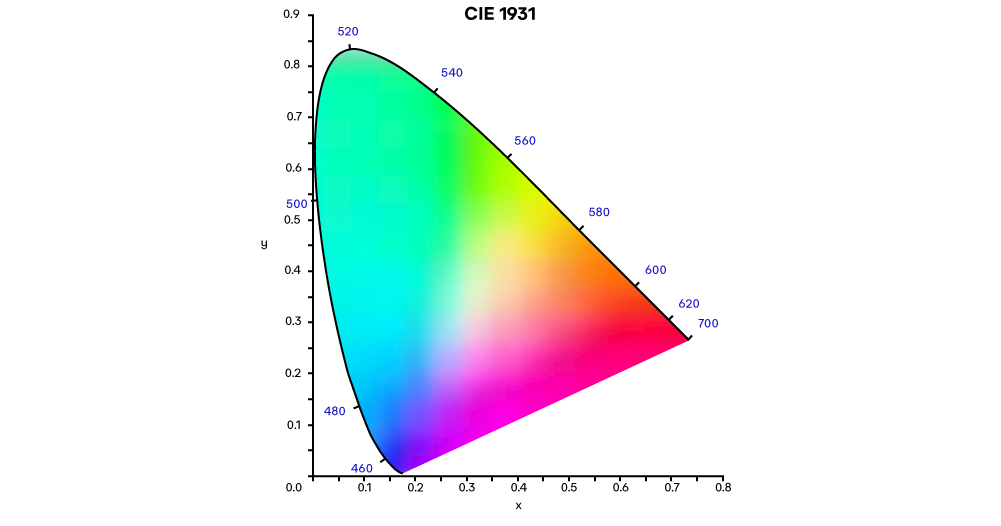
2.2 色度坐标与马蹄图

由于 $Y$ 代表亮度，为了分离出色度（Chromaticity）信息，我们进行归一化：

$$
x = \frac{X}{X+Y+Z}, \quad y = \frac{Y}{X+Y+Z}
$$

这构成了著名的 CIE 1931 色度图（马蹄图）。任何物理上存在的颜色都落在这个马蹄形区域内。

---

第三部分：感知均匀性与 CIELAB 空间

CIE 1931 XYZ 空间最大的问题是感知不均匀性。在色度图上的不同区域，相同几何距离（Euclidean Distance）所代表的人眼感知色差是巨大的。例如，在绿色区域移动 0.1 的距离可能人眼难以察觉，但在蓝色区域移动 0.1 则是巨大的颜色变化。

麦克亚当（MacAdam）通过实验绘制了麦克亚当椭圆，直观地展示了这种不均匀性。为了解决这个问题，我们需要对 XYZ 空间进行非线性变换，使其接近“感知均匀”。这就是 *CIELAB ($L^a^b^$) 空间。

3.1 XYZ 到 Lab 的非线性变换

CIELAB 旨在使得空间中的欧几里得距离与人眼的感知色差成正比。其核心是引入了立方根函数来模拟人眼对亮度的非线性响应（韦伯-费希纳定律）。

定义参考白点为 $(X_n, Y_n, Z_n)$，则：

$$
L^* = 116 f(Y/Y_n) - 16
$$

$$
a^* = 500 [f(X/X_n) - f(Y/Y_n)]
$$

$$
b^* = 200 [f(Y/Y_n) - f(Z/Z_n)]
$$

其中函数 $f(t)$ 定义为：

$$
f(t) = \begin{cases}
t^{1/3} & \text{if } t > (\frac{6}{29})^3 \
\frac{1}{3}(\frac{29}{6})^2 t + \frac{4}{29} & \text{otherwise}
\end{cases}
$$

• $L^*$：亮度（0黑 - 100白）。
• $a^*$：红-绿轴（正红负绿）。
• $b^*$：黄-蓝轴（正黄负蓝）。

---

第四部分：色差公式 ($\Delta E$) —— 差异的度量

一旦我们在均匀色彩空间中拥有了坐标，计算两个颜色样本之间的差异（色差）就变成了计算空间中两点间的距离。

4.1 $\Delta E^*_{ab}$ (CIE76)

这是最基础的色差公式，即 Lab 空间中的欧几里得距离：

$$
\Delta E^_{ab} = \sqrt{(\Delta L^)^2 + (\Delta a^)^2 + (\Delta b^)^2}
$$

通常认为 $\Delta E^*_{ab} \approx 2.3$ 是人眼的恰可察觉差（JND, Just Noticeable Difference），但在严格的工业应用中，$\Delta E < 1.0$ 通常被视为优秀。

4.2 进阶：$\Delta E_{00}$ (CIEDE2000)

虽然 Lab 空间比 XYZ 均匀，但仍不完美。特别是在高饱和度区域和蓝色区域，简单的欧几里得距离仍不能完美反映人眼感受。$\Delta E_{00}$ 引入了极为复杂的加权函数（$S_L, S_C, S_H$）和旋转项（$R_T$）来修正这些偏差。它是目前最精确的色差公式，但也最难计算。

---

第五部分：色彩不均匀性（Uniformity）的计算方法

在显示器制造（LCD, OLED, Micro-LED）或照明工程中，不均匀性（Non-uniformity），常被称为 Mura，是一个关键质量指标。

不均匀性分为两类：亮度不均匀性和色度不均匀性。

5.1 采样策略

首先，必须定义空间采样点。工业标准（如 VESA FPDM 或 IDMS）通常建议使用 9点、13点或 25点阵列覆盖显示区域。

设采样点集合为 $P = {p_1, p_2, …, p_N}$，每个点 $p_i$ 测量得到的数据为 $(L^_i, a^_i, b^*_i)$ 或 $(Y_i, x_i, y_i)$。

5.2 亮度不均匀性计算

亮度通常只关注 $Y$ 值（或 $L_v$，单位 $cd/m^2$）。

最常用的度量是最大亮度偏差率：

$$
Uniformity_{Lum} = 1 - \frac{L_{min}}{L_{max}}
$$

或者根据 ANSI 标准使用百分比表示：

$$
ANSI\ Uniformity = \frac{L_{min}}{L_{max}} \times 100%
$$

其中 $L_{min}$ 和 $L_{max}$ 是所有采样点中的最小和最大亮度值。

5.3 色彩不均匀性计算

色彩不均匀性比亮度更复杂，因为它涉及色度漂移。常用的计算方法是最大色差法。

方法 A：相对于中心点的偏差 ($\Delta E_{center}$)

这是最严格的方法。计算所有点相对于屏幕中心点 $p_{center}$ 的色差。

$$
\Delta E_i = \sqrt{(L^_i - L^_{center})^2 + (a^_i - a^_{center})^2 + (b^_i - b^_{center})^2}
$$

$$
NonUniformity_{color} = \max_{i \in P} (\Delta E_i)
$$

方法 B：最大成对偏差 ($\Delta E_{max-pair}$)

计算网格中任意两点之间的最大色差。这代表了屏幕上可能出现的最糟糕的颜色差异。

$$
NonUniformity_{global} = \max_{i,j} \left( \sqrt{(L^_i - L^_j)^2 + (a^_i - a^_j)^2 + (b^_i - b^_j)^2} \right)
$$

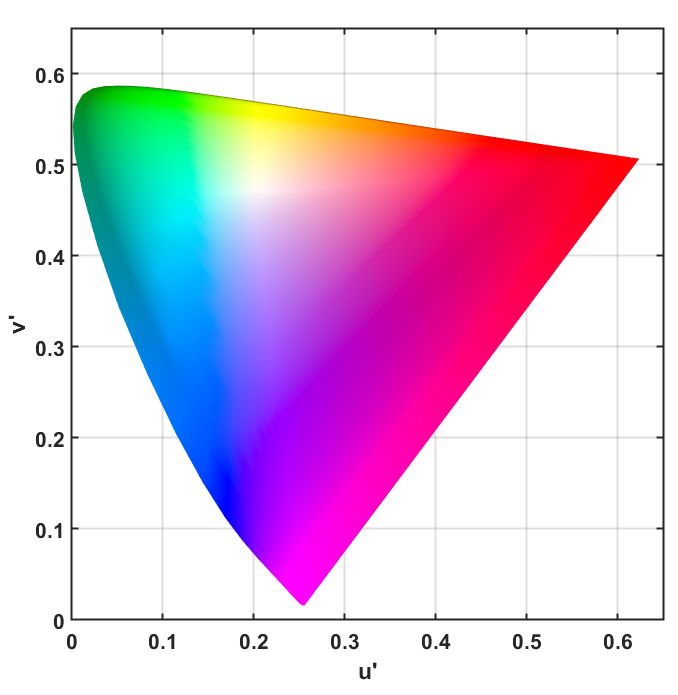
方法 C：$\Delta u’v’$ 均匀性

对于某些应用，我们只关心色度（Colorimetry）而不关心亮度。此时应使用 CIE 1976 UCS 图 ($(u’, v’)$) 中的距离。

$$
\Delta C_i = \sqrt{(u’i - u’{center})^2 + (v’i - v’{center})^2}
$$

通常要求 $\Delta u’v’ < 0.005$ 或更严格。

---

第六部分：算法实现示例（MATLAB）

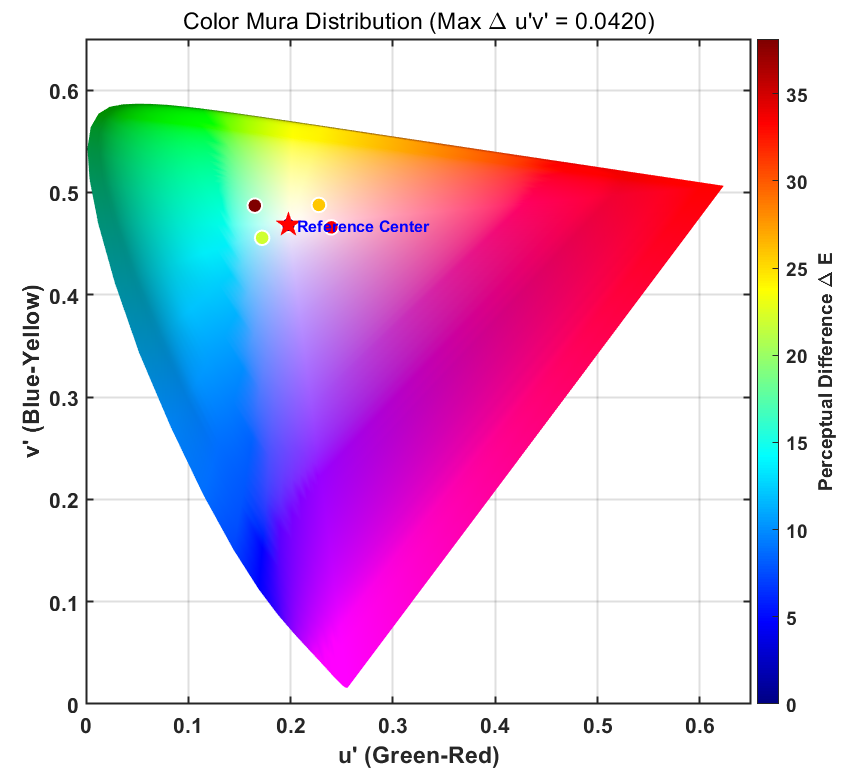
在工程实践中，单纯的数值列表往往难以直观反映人眼对屏幕整体均匀性的感受。我们需要将计算结果映射回二维色彩空间，结合色度图来分析 Mura 的分布特征。

以下代码（基于 MATLAB Image Processing Toolbox）实现了从 XYZ 数据到 $\Delta E$ 和 $\Delta u’v’$ 的完整计算流程，并采用了一种“多维可视化”策略：空间位置代表色度坐标，点的大小与颜色代表色差幅度。

function [results] = analyze_color_uniformity_advanced(xyz_data)
    % 输入: xyz_data (N x 3 矩阵, 列分别为 X, Y, Z)
    % 假设第一行为中心参考点
    
    % 1. 提取基础分量并计算 u', v'
    X = xyz_data(:, 1); Y = xyz_data(:, 2); Z = xyz_data(:, 3);
    denom = X + 15*Y + 3*Z;
    u_prime = 4*X ./ denom;
    v_prime = 9*Y ./ denom;
    
    % 2. 计算色差与色偏移
    ref_u = u_prime(1); ref_v = v_prime(1);
    duv = sqrt((u_prime - ref_u).^2 + (v_prime - ref_v).^2);
    
    % 计算 CIELAB (D65)
    lab_data = xyz2lab(xyz_data, 'WhitePoint', [95.047, 100.000, 108.883]);
    dE = sqrt(sum((lab_data - lab_data(1,:)).^2, 2));
    
    % 3. 可视化绘制
    figure('Color', 'w', 'Position', [100, 100, 800, 600]);
    hold on;
    
    % 绘制底图（局部聚焦模式）
    try
        plotChromaticity('ColorSpace', 'uv'); 
    catch
        % 若无工具箱，绘制简易光谱轨迹边界（略）
    end
    
    % 绘制采样点 - 使用较大的 Marker 和透明度边缘以便区分
    scatter(u_prime, v_prime, 120, dE, 'filled', 'MarkerEdgeColor', 'w', 'LineWidth', 1.5);
    
    % 强化参考点显示
    plot(ref_u, ref_v, 'rp', 'MarkerSize', 18, 'MarkerFaceColor', 'r');
    text(ref_u, ref_v, '  Reference Center', 'FontSize', 12, 'FontWeight', 'bold', 'Color', 'b');
    
    % --- 核心优化：动态调整视口，拉开视觉距离 ---
    padding = 0.05; % 增加 5% 的边缘留白
    % u_range = [min(u_prime)-padding, max(u_prime)+padding];
    % v_range = [min(v_prime)-padding, max(v_prime)+padding];
    % axis([u_range v_range]); 
    
    % 辅助修饰
    colormap(jet);
    cb = colorbar;
    ylabel(cb, 'Perceptual Difference \Delta E');
    xlabel('u'' (Green-Red)'); ylabel('v'' (Blue-Yellow)');
    title(['Color Mura Distribution (Max \Delta u''v'' = ', num2str(max(duv), '%.4f'), ')']);
    grid on; box on;
end

% --- 仿真测试：构造“拉开距离”的数据 ---
% 模拟不同方位的色偏点，确保在坐标系中呈现发散状
test_xyz = [
    95.04, 100.00, 108.88; % 1. 中心参考点 (White)
    105.0, 100.00, 80.00;  % 2. 显著偏黄/绿
    85.00, 100.00, 130.0;  % 3. 显著偏蓝/紫
    110.0, 95.00,  100.0;  % 4. 显著偏红
    80.00, 105.0,  95.00   % 5. 显著偏青
];

analyze_color_uniformity_advanced(test_xyz);

运行结果如图