深入解析薄膜干涉：从物理本源到算法仿真

薄膜干涉（Thin Film Interference）不仅是物理学中最迷人的现象之一——赋予了肥皂泡斑斓的色彩和昆虫翅膀金属般的光泽——更是现代精密光学的基石。从相机镜头上的抗反射涂层（AR Coating）到光刻机中的极紫外反射镜，这一机制支撑着现代光电子产业的半壁江山。

本文将摒弃浅尝辄止的现象描述，从光波叠加的原理出发，推导干涉条件的数学本质，进而引入处理复杂多层膜系统的传输矩阵法（Transfer Matrix Method, TMM），最后通过 Matlab 代码演示如何仿真并优化一个光学薄膜系统。

1. 物理本源：光波的叠加与相位

要理解薄膜干涉，我们必须回归光的波动性。当光从一种介质传播到另一种介质时，在界面处会发生反射和折射。薄膜干涉的核心在于：从薄膜上下两个表面反射的光波，在空间中重叠并发生干涉。

1.1 光程差（Optical Path Difference, OPD）

假设一束单色光以入射角 $\theta_1$ 照射到折射率为 $n_2$、厚度为 $d$ 的薄膜上，薄膜上下方的介质折射率分别为 $n_1$ 和 $n_3$。

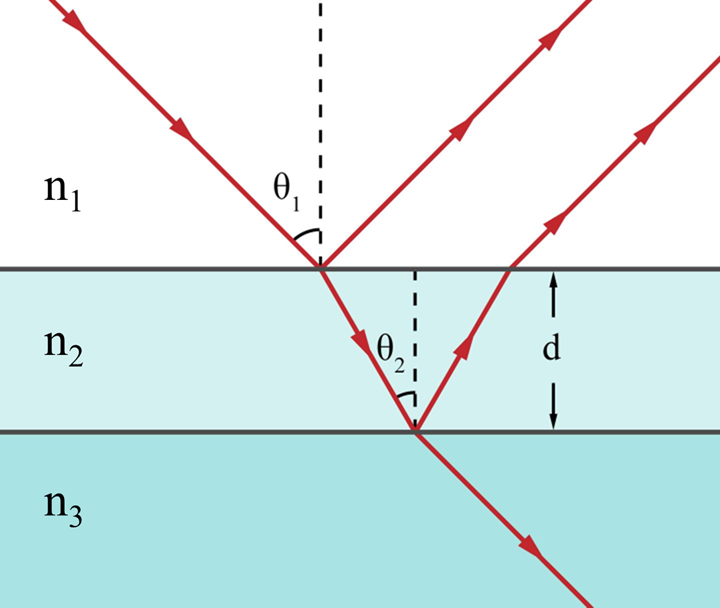
薄膜干涉光路示意图

光在薄膜内部传播的几何路径长度并非简单的 $2d$，而是经过折射角 $\theta_2$ 修正后的路径。通过几何推导，上下两个表面反射光束的光程差 $\Delta$ 为：

$$
\Delta = 2 n_2 d \cos(\theta_2)
$$

1.2 半波损失（Half-wave Loss）

除了几何路程引起的相位差，我们必须考虑界面反射引起的相位突变。根据菲涅尔方程（Fresnel Equations）：

  • 光疏介质射向光密介质（$n_1 < n_2$）：反射光发生 $\pi$（即 $180^\circ$）的相位突变，相当于增加了 $\lambda/2$ 的光程。
  • 光密介质射向光疏介质（$n_1 > n_2$）：反射光无相位突变。

因此，对于最常见的空气($n_1$)-薄膜($n_2$)-玻璃($n_3$)结构，且 $n_1 < n_2 < n_3$ 时，上下两个界面均发生半波损失，相对相位差抵消。但在 $n_1 < n_2 > n_3$ 的情形下（如肥皂泡），只有上表面发生半波损失。

1.3 干涉条件：相消与相长的物理判据

干涉的本质是波的叠加。为了确定薄膜表面呈现的是亮色（增强）还是暗色（抵消），我们必须从**总光程差（Total Optical Path Difference, $\delta$）**入手。

1.3.1 总光程差的构成

总光程差 $\delta$ 由两部分组成：几何路径引起的光程差，以及界面反射引起的相位突变（即半波损失）带来的附加光程差。

$$
\delta = \delta_{geom} + \delta_{phase}
$$

  1. 几何光程差 ($\delta_{geom}$)：
    光在折射率为 $n_2$ 的薄膜中往返一次，考虑到折射角 $\theta_2$，其几何光程差为：
    $$
    \delta_{geom} = 2 n_2 d \cos(\theta_2)
    $$

  2. 相位附加光程差 ($\delta_{phase}$)：
    这取决于上下两个界面反射性质的差异。

    • 若两个界面都发生（或都不发生）半波损失，则相对相位差为 0，$\delta_{phase} = 0$。
    • 若仅有一个界面发生半波损失，则相对相位差为 $\pi$，相当于光程增加了半个波长，$\delta_{phase} = \pm \frac{\lambda}{2}$。

1.3.2 核心干涉判据

无论具体的介质如何，波的叠加原理给出了永恒不变的判据：

  • 干涉相长 (Constructive Interference)：
    当总光程差是波长的整数倍时，波峰与波峰叠加，反射光最强（亮纹）。
    $$
    \delta = m\lambda \quad (m=1, 2, 3…)
    $$

  • 干涉相消 (Destructive Interference)：
    当总光程差是半波长的奇数倍时，波峰与波谷叠加，反射光最弱（暗纹）。
    $$
    \delta = (m + \frac{1}{2})\lambda \quad (m=0, 1, 2…)
    $$

1.3.3 两种典型介质结构的推导

结合上述判据与 $\delta_{phase}$ 的不同，我们可以用两个实际案例展开来看：

场景 A：相位异号层叠（如：肥皂泡、油膜）

  • 结构特征：$n_1 < n_2 > n_3$（中间折射率最大）。
  • 相位分析：上表面反射有半波损失，下表面没有。$\delta_{phase} = \frac{\lambda}{2}$。
  • 推导结果：
    • 相长（亮）：几何光程差需补偿那半个波长，凑成整数。
      $$2 n_2 d \cos \theta_2 = (m + \frac{1}{2})\lambda$$
    • 相消（暗）：几何光程差本身即为整数波长，加上 $\frac{\lambda}{2}$ 后正好相消。
      $$2 n_2 d \cos \theta_2 = m\lambda$$

场景 B：相位同号层叠（如：镜头增透膜 AR Coating）

  • 结构特征：$n_1 < n_2 < n_3$（折射率逐层递增）。
  • 相位分析：上下表面均发生半波损失，相对差值为 0。$\delta_{phase} = 0$。
  • 推导结果：
    • 相长（亮）：几何光程差直接等于整数波长。
      $$2 n_2 d \cos \theta_2 = m\lambda$$
    • 相消（暗）：几何光程差需提供半个波长的差值。
      $$2 n_2 d \cos \theta_2 = (m + \frac{1}{2})\lambda$$

1.3.4 总结与能量守恒

为了方便工程应用，我们可以将上述结论总结如下表：

物理场景 折射率关系 界面相变差 干涉相消 (暗) 条件
(Destructive)		 干涉相长 (亮) 条件
(Constructive)
增透膜 $n_1 < n_2 < n_3$ $0$ $2n_2d\cos\theta_2 = (m+\frac{1}{2})\lambda$ $2n_2d\cos\theta_2 = m\lambda$
肥皂泡 $n_1 < n_2 > n_3$ $\lambda/2$ $2n_2d\cos\theta_2 = m\lambda$ $2n_2d\cos\theta_2 = (m+\frac{1}{2})\lambda$

2. 进阶理论：传输矩阵法 (Transfer Matrix Method)

对于简单的单层膜，几何推导尚能胜任。但面对现代光学中动辄几十层的复杂膜系（如高反膜、截止滤光片），我们需要一种能够系统化处理多重界面反射的数学工具。

这就是传输矩阵法（TMM）。它的核心思想是将每一层薄膜视为一个线性变换矩阵，通过矩阵连乘，将复杂的多层结构简化为一个单一的“等效界面”。

2.1 核心概念：光学导纳 (Optical Admittance)

在深入矩阵之前，我们必须先理解导纳 (Admittance)。在电学中，导纳是阻抗的倒数（$Y = 1/Z$），描述介质导通电流的能力；在波动光学中，导纳描述介质对光波（电磁场）的响应能力。

2.1.1 从物理导纳到光学导纳

根据麦克斯韦方程组，绝对导纳定义为磁场强度 $H$ 与电场强度 $E$ 的比值：

$$Y = \frac{H}{E} = \sqrt{\frac{\epsilon}{\mu}}$$

  • 在真空（自由空间）中：
    介电常数 $\epsilon_0$ 和磁导率 $\mu_0$ 决定了真空的特性阻抗。真空导纳是一个物理常数：
    $$\mathcal{Y}_0 = \sqrt{\frac{\epsilon_0}{\mu_0}} \approx \frac{1}{377} , \text{S} , (\text{西门子})$$
    (注：这里的 S 代表西门子 Siemens，即 $\Omega^{-1}$。但在光学工程中，为了避免繁琐的常数运算，我们通常不直接使用这个带单位的数值。)

  • 在介质中：
    对于绝大多数光学材料（非磁性，$\mu_r \approx 1$），其绝对导纳为：
    $$Y = \sqrt{\frac{\epsilon_0 \epsilon_r}{\mu_0}} = \sqrt{\epsilon_r} \mathcal{Y}_0 = n \mathcal{Y}_0$$

归一化处理：
为了计算方便，我们定义光学导纳 $\eta$ 为绝对导纳与真空导纳的比值。这样，光学导纳就变成了一个无量纲的量，数值上等于折射率：
$$\eta_{norm} = \frac{Y}{\mathcal{Y}_0} = n$$

2.1.2 倾斜入射时的修正导纳

当光以角度 $\theta$ 倾斜入射时，我们需要考虑边界条件。电磁场理论要求：只有平行于界面的场分量（切向分量）才是连续的。

因此，我们定义的“有效导纳”必须是切向磁场 $H_{\parallel}$ 与切向电场 $E_{\parallel}$ 之比。由于电场和磁场相互垂直，当光线倾斜时，E 和 H 投影到界面上的分量会发生不同的变化，导致 S 偏振和 P 偏振的公式不同。

  • S-偏振 (TE波)：
    电场 $E$ 垂直于入射面（完全平行于界面），而磁场 $H$ 倾斜。

    • 切向电场：$E_{\parallel} = E$
    • 切向磁场：$H_{\parallel} = H \cos \theta$
    • 修正导纳：
      $$\eta_s = \frac{H_{\parallel}}{E_{\parallel}} = \frac{H \cos \theta}{E} = \eta_{norm} \cos \theta = n \cos \theta$$

  • P-偏振 (TM波)：
    磁场 $H$ 垂直于入射面（完全平行于界面），而电场 $E$ 倾斜。

    • 切向磁场：$H_{\parallel} = H$
    • 切向电场：$E_{\parallel} = E \cos \theta$
    • 修正导纳：
      $$\eta_p = \frac{H_{\parallel}}{E_{\parallel}} = \frac{H}{E \cos \theta} = \frac{\eta_{norm}}{\cos \theta} = \frac{n}{\cos \theta}$$

物理直觉总结：

  • 数值上：你可以简单地认为导纳就是折射率 $n$，只是根据角度做了 $\cos\theta$ 的修正。
  • 物理上：导纳匹配（$\eta_1 = \eta_2$）意味着没有反射。这也解释了为什么存在布鲁斯特角 (Brewster’s Angle)：对于 P 偏振，当 $\eta_{p1} = \eta_{p2}$ 即 $\frac{n_1}{\cos\theta_1} = \frac{n_2}{\cos\theta_2}$ 时，反射率降为 0。

2.2 单层薄膜的特征矩阵

根据麦克斯韦方程组，电磁波在跨越介质边界时，电场切向分量 $E$ 和磁场切向分量 $H$ 必须保持连续。

想象光波穿过第 $j$ 层薄膜。我们可以建立该层“输入表面”的场 $(E_{in}, H_{in})$ 与“输出表面”的场 $(E_{out}, H_{out})$ 之间的线性关系：

$$
\begin{bmatrix}
E_{in} \
H_{in}
\end{bmatrix}

M_j
\begin{bmatrix}
E_{out} \
H_{out}
\end{bmatrix}
$$

这里的 $M_j$ 就是第 $j$ 层的特征矩阵：

$$
M_j = \begin{bmatrix}
\cos \delta_j & \frac{i}{\eta_j} \sin \delta_j \
i \eta_j \sin \delta_j & \cos \delta_j
\end{bmatrix}
$$

其中：

  • $i$ 是虚数单位（代表相位的旋转）。
  • $\delta_j = \frac{2\pi}{\lambda} n_j d_j \cos \theta_j$ 是光穿过该层产生的相位厚度。

2.3 系统总矩阵与“等效介质”

对于一个由 $N$ 层薄膜堆叠而成的系统，光依次穿过每一层。根据线性代数的结合律，整个系统的总传输矩阵 $M$ 就是各层矩阵的乘积：

$$
M = M_1 \cdot M_2 \cdot \dots \cdot M_N = \begin{bmatrix}
m_{11} & m_{12} \
m_{21} & m_{22}
\end{bmatrix}
$$

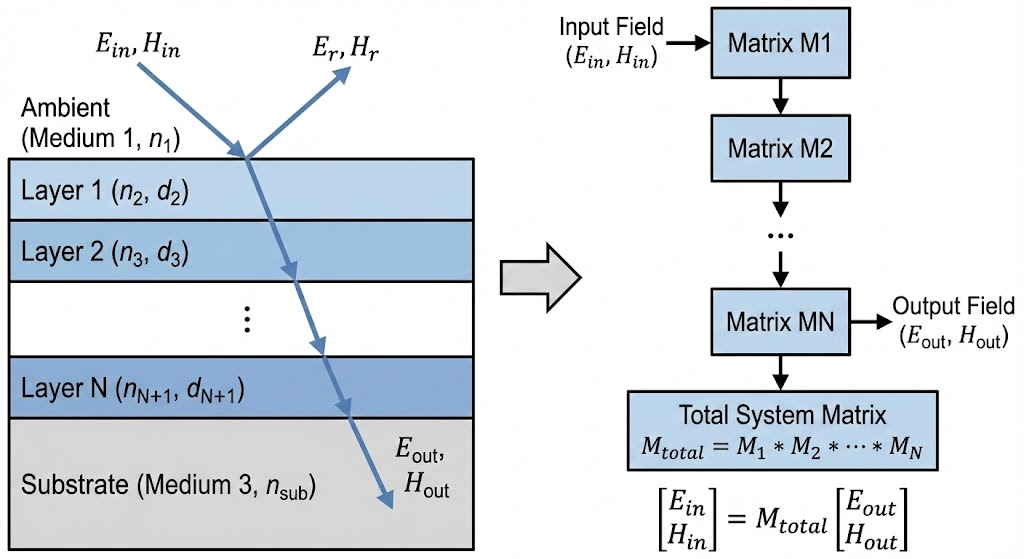
这一步的物理意义极其重大：它意味着，无论中间有多少层复杂的薄膜，我们都可以把它们看作一个黑盒。这个黑盒把最底层的基底（Substrate）包裹起来，形成了一个具有等效导纳 $Y$ 的新虚拟介质。

我们可以通过总矩阵计算这个系统的等效导纳 $Y$。假设基底的导纳为 $\eta_{sub}$，则：

$$
\begin{bmatrix}
E_{total} \
H_{total}
\end{bmatrix}
= M
\begin{bmatrix}
1 \
\eta_{sub}
\end{bmatrix}
$$
(注：这里假设基底处的电场归一化为 1，则磁场为 $\eta_{sub}$)

由此得到系统的等效导纳 $Y$ 为输入端的磁场与电场之比：

$$
Y = \frac{H_{total}}{E_{total}} = \frac{m_{21} + m_{22}\eta_{sub}}{m_{11} + m_{12}\eta_{sub}}
$$

2.4 计算透射率 (T) 与反射率 (R)

一旦求出了这个等效导纳 $Y$，复杂的多层膜问题瞬间退化为最简单的单界面反射问题：光从入射介质（导纳 $\eta_0$）射向一个导纳为 $Y$ 的等效介质。

1. 反射系数 (Reflection Coefficient, $r$)
这是反射波振幅与入射波振幅的比值：
$$
r = \frac{\eta_0 - Y}{\eta_0 + Y}
$$

2. 能量反射率 (Reflectance, $R$)
这是我们肉眼看到或探测器测到的能量比率：
$$
R = |r|^2 = \left( \frac{\eta_0 - Y}{\eta_0 + Y} \right) \overline{\left( \frac{\eta_0 - Y}{\eta_0 + Y} \right)}
$$

3. 能量透射率 (Transmittance, $T$)
如果薄膜介质没有吸收（消光系数 $k=0$），根据能量守恒：
$$
T = 1 - R
$$
如果存在吸收，则通过矩阵元直接计算透射系数 $t$ 更为准确：
$$
t = \frac{2\eta_0}{\eta_0(m_{11} + m_{12}\eta_{sub}) + (m_{21} + m_{22}\eta_{sub})}
$$
$$
T = \frac{\text{Re}(\eta_{sub})}{\text{Re}(\eta_0)} |t|^2
$$

至此，我们将复杂的多层膜物理过程，完全转化为了计算机擅长的矩阵运算。这就是 TMM 算法为何如此强大的原因。

3. 工程仿真：MATLAB 实现与可视化

理论必须通过实践来验证。MATLAB 凭借其原生的矩阵运算能力，是处理传输矩阵法（TMM）的最佳工具。在本节中，我们将从简单的单层抗反射膜入手，逐步进阶到复杂的多层高反膜系设计。

3.1 核心算法：通用光学求解器

首先，我们需要封装一个通用的计算函数。为了获得完整的物理图像，该函数将同时计算反射率 (R) 和透射率 (T)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
function [R, T] = calculate_optical_properties(lambda, n_stack, d_stack, theta_inc)
    % calculate_optical_properties 使用传输矩阵法计算多层膜 R 和 T
    % 输入:
    %   lambda:    入射波长向量 (nm)
    %   n_stack:   各层折射率向量 [n_air, n_1, ..., n_sub]
    %   d_stack:   各层厚度向量 (nm) [0, d_1, ..., 0] (首尾为0)
    %   theta_inc: 入射角 (弧度)
    % 输出:
    %   R: 反射率 (Energy Reflectance)
    %   T: 透射率 (Energy Transmittance)
    
    num_points = length(lambda);
    R = zeros(1, num_points);
    T = zeros(1, num_points);
    
    for k = 1:num_points
        curr_lambda = lambda(k);
        
        % 1. 斯涅尔定律求各层角度
        % n0*sin(th0) = ni*sin(thi)
        n0 = n_stack(1);
        theta_list = asin( (n0 * sin(theta_inc)) ./ n_stack );
        
        % 2. 计算修正导纳 (此处演示 S-Polarization / TE Mode)
        % 若需 P-Polarization，公式改为: eta = n ./ cos(theta)
        eta_list = n_stack .* cos(theta_list);
        
        % 3. 矩阵连乘
        M_total = [1, 0; 0, 1];
        
        % 遍历中间薄膜层 (索引 2 到 end-1)
        for j = 2:(length(n_stack)-1)
            nj = n_stack(j);
            dj = d_stack(j);
            thj = theta_list(j);
            eta_j = eta_list(j);
            
            % 相位厚度
            delta = 2 * pi * nj * dj * cos(thj) / curr_lambda;
            
            % 特征矩阵 Mj
            M_layer = [cos(delta),      (1i / eta_j) * sin(delta); ...
                       1i * eta_j * sin(delta), cos(delta)];
            
            % 左乘积累
            M_total = M_total * M_layer;
        end
        
        % 4. 计算特征向量 [B; C] 并求解 R, T
        eta_sub = eta_list(end);
        BC = M_total * [1; eta_sub];
        B = BC(1); 
        C = BC(2);
        
        % 计算反射率 R
        eta_0 = eta_list(1);
        Y = C / B; % 输入光学导纳
        R(k) = abs((eta_0 - Y)/(eta_0 + Y))^2;
        
        % 计算透射率 T (严谨公式，适用于含吸收介质)
        % 透射系数 t = 2*eta0 / (eta0*B + C)
        t_coeff = (2 * eta_0) / (eta_0 * B + C);
        T(k) = real(eta_sub) / real(eta_0) * abs(t_coeff)^2;
    end
end

3.2 仿真案例一：单层增透膜 (AR Coating) 分析

在这个案例中，我们将模拟经典的氟化镁 ($MgF_2$) 镀在玻璃上的场景。我们将完成两项任务：

  1. 光谱对比：直观展示镀膜前后，玻璃透光率的提升。
  2. 公差分析：通过扫描膜层厚度，生成反射率地形图，分析工艺误差对性能的影响。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
% === 脚本 1: 单层 AR 膜仿真 ===
clear; clc; close all;

% --- A. 参数定义 ---
lambda_range = linspace(400, 800, 500); % 可见光波段
n_air = 1.0;
n_MgF2 = 1.38;
n_Glass = 1.52;
% 最佳设计厚度：针对 550nm (绿光) 优化的 1/4 波长 (~99.6nm)
d_opt = 550 / (4 * n_MgF2); 

% --- B. 光谱计算 ---
% 1. 裸玻璃 (Bare Glass)
[R_bare, ~] = calculate_optical_properties(lambda_range, ...
    [n_air, n_Glass], [0, 0], 0);

% 2. 镀膜玻璃 (Coated Glass)
[R_ar, ~] = calculate_optical_properties(lambda_range, ...
    [n_air, n_MgF2, n_Glass], [0, d_opt, 0], 0);

% --- C. 参数扫描 (厚度 vs 波长) ---
d_scan = linspace(0, 300, 300); % 扫描 0-300nm 厚度
R_map = zeros(length(d_scan), length(lambda_range));

h = waitbar(0, '正在计算地形图...');
for i = 1:length(d_scan)
    [r_temp, ~] = calculate_optical_properties(lambda_range, ...
        [n_air, n_MgF2, n_Glass], [0, d_scan(i), 0], 0);
    R_map(i, :) = r_temp;
    if mod(i, 50) == 0; waitbar(i/length(d_scan), h); end
end
close(h);

% --- D. 综合可视化 ---
figure('Color', 'w', 'Position', [100, 100, 1000, 500]);

% 左图：光谱对比
subplot(1, 2, 1);
plot(lambda_range, R_bare*100, 'r--', 'LineWidth', 1.5); hold on;
plot(lambda_range, R_ar*100, 'b-', 'LineWidth', 2);
title('光谱对比: 有无增透膜', 'FontSize', 12);
xlabel('波长 (nm)'); ylabel('反射率 (%)');
legend('裸玻璃 (约4.2%)', '镀MgF_2膜 (最低1.2%)');
grid on; axis([400 800 0 6]);

% 右图：参数扫描地形图
subplot(1, 2, 2);
imagesc(lambda_range, d_scan, R_map*100);
colormap(jet); 
cb = colorbar; cb.Label.String = 'Reflectance (%)';
set(gca, 'YDir', 'normal'); % 坐标轴方向修正

% 标记最佳设计点
hold on; yline(d_opt, 'w--', 'LineWidth', 2); 
text(420, d_opt+20, ['设计厚度 d \approx ' num2str(round(d_opt)) 'nm'], ...
    'Color', 'w', 'FontWeight', 'bold');

title('反射率地形图 (厚度敏感度)', 'FontSize', 12);
xlabel('波长 (nm)'); ylabel('膜层厚度 (nm)');

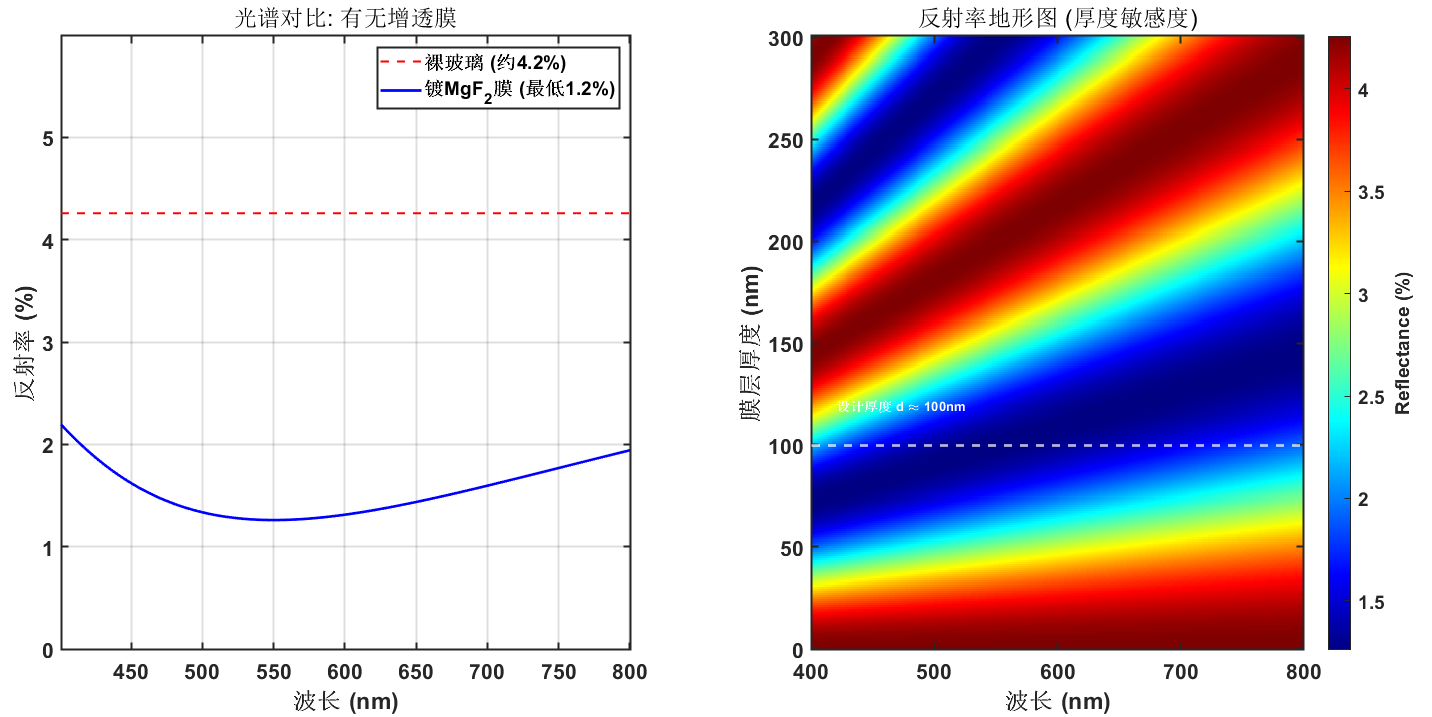
结果解读：

  • 左图展示了“相消干涉”的威力：在设计中心波长 550nm 处，反射率显著下降。
  • 右图则揭示了物理规律：深蓝色的低反射区域呈现倾斜状。这意味着，如果镀膜工艺变厚了（向上移动），最佳抗反射波长也会向红光方向移动（红移）。

3.3 仿真案例二：多层布拉格反射镜 (Bragg Mirror)

TMM 的真正强大之处在于处理多层膜。这里我们设计一个 分布布拉格反射镜 (DBR)。通过交替堆叠高折射率（$n_H$）和低折射率（$n_L$）材料，每层厚度均为 $1/4$ 波长，我们可以利用相长干涉制造出反射率接近 100% 的“完美镜子”。

  • 材料：$TiO_2$ ($n_H=2.4$) 和 $SiO_2$ ($n_L=1.46$)
  • 结构：玻璃基底 + 10 对 $(HL)$ + 空气
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
% === 脚本 2: 多层 DBR 高反膜仿真 ===
% 1. DBR 设计参数
lambda_center = 600; % 设计中心波长 (橙光)
n_H = 2.4;  d_H = lambda_center / (4 * n_H); % TiO2
n_L = 1.46; d_L = lambda_center / (4 * n_L); % SiO2
N_pairs = 10; % 堆叠对数

% 2. 构建多层堆栈向量
% 结构: Air | H L H L ... H L | Glass
n_stack = [n_air]; 
d_stack = [0];

for i = 1:N_pairs
    n_stack = [n_stack, n_H, n_L];
    d_stack = [d_stack, d_H, d_L];
end

n_stack = [n_stack, n_Glass];
d_stack = [d_stack, 0];

% 3. 运行仿真
[R_dbr, T_dbr] = calculate_optical_properties(lambda_range, n_stack, d_stack, 0);

% 4. 可视化
figure('Color', 'w', 'Position', [150, 150, 800, 400]);
area(lambda_range, R_dbr*100, 'FaceColor', [0.85 0.33 0.1], 'EdgeColor', 'none', 'FaceAlpha', 0.8); 
hold on;
plot(lambda_range, T_dbr*100, 'k-', 'LineWidth', 1.5);

title(['10对 TiO_2/SiO_2 布拉格反射镜 (中心波长 ' num2str(lambda_center) 'nm)'], 'FontSize', 12);
xlabel('波长 (nm)'); ylabel('比率 (%)');
legend('反射率 R', '透射率 T', 'Location', 'east');
grid on; ylim([0 105]);

% 标注“禁带”宽度
text(lambda_center, 50, '光子禁带 (Stopband)', ...
     'HorizontalAlignment', 'center', 'FontSize', 12, 'FontWeight', 'bold', 'Color', 'w');

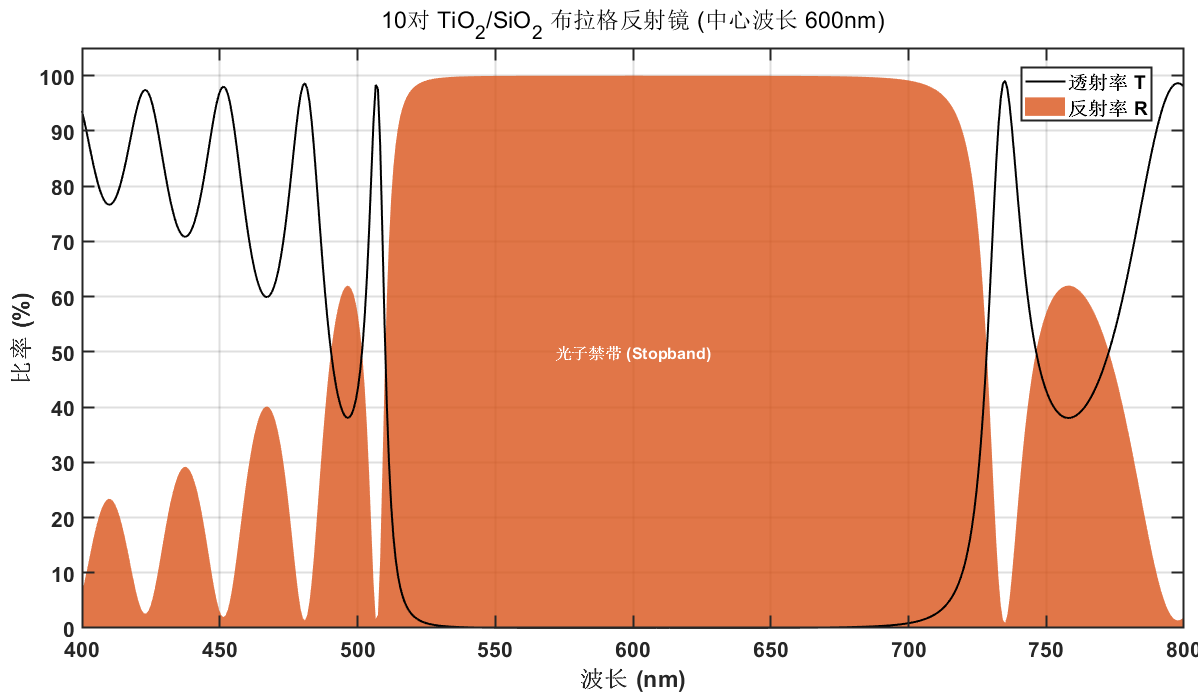
仿真结果：
你将看到一个宽阔的**“高反平顶区” (Stopband)**。在这个波段内，光无法穿透薄膜，几乎被全反射。这就是激光器谐振腔镜片和高档介质反射镜的工作原理。通过简单地增加层数 $N$，我们可以让反射率无限接近 100%，这是金属反射镜无法做到的。

4. 逆向设计：基于梯度的优化 (Optimization)

在实际工程中，我们面临的往往是逆向问题：给定目标光谱（例如 400-700nm 全波段反射率 < 0.5%），求各层薄膜的最佳厚度。

对于 4 层宽带增透膜（BBAR），只要膜系结构设计合理，基于梯度的局部优化算法 fmincon 就足以找到完美的全局最优解，且速度极快。

4.1 核心策略：结构修正与多起点搜索

黄金法则：为了降低初始界面反射，最外层（接触空气层）必须是低折射率材料 (L)。
我们将采用 Air | L | H | L | H | Glass 的结构。如果错误地以高折射率 ($H$) 开头，优化器将极难收敛到 < 0.5% 的目标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
% === 脚本 3: 宽带增透膜(BBAR) 逆向优化 ===
clear; clc; close all;

% 1. 优化目标设定
% 重点优化 400-700nm，增加采样点以提高精度
lambda_opt = linspace(400, 700, 50); 
target_R = zeros(size(lambda_opt));  % 目标：全波段 0 反射

% 2. 结构定义 (关键修正: L-first 结构)
% Air(1.0) | L(1.46) | H(2.4) | L(1.46) | H(2.4) | Glass(1.52)
n_air = 1.0; n_L = 1.46; n_H = 2.4; n_sub = 1.52;
% 注意顺序：Air 后面紧跟的是 n_L
n_stack_fixed = [n_air, n_L, n_H, n_L, n_H, n_sub];
num_layers = 4;

% 3. 定义优化器
lb = ones(1, num_layers) * 10;  % 厚度下限 10nm
ub = ones(1, num_layers) * 300; % 厚度上限 300nm

% 损失函数: 使用 Sum of Squares (SSE)
cost_func = @(x) sum((calculate_optical_properties(lambda_opt, ...
    n_stack_fixed, [0, x, 0], 0) - target_R).^2);

options = optimoptions('fmincon', 'Display', 'none', ...
    'Algorithm', 'sqp', 'StepTolerance', 1e-12);

% --- 多起点全局搜索 (Multi-start) ---
% 防止掉入局部陷阱，我们随机尝试 20 个起点
fprintf('正在启动多起点梯度优化 (L-first 结构)...\n');
best_loss = inf;
best_x = [];

for i = 1:20
    % 随机生成初始猜测
    x0_random = 20 + (250-20) * rand(1, num_layers);
    
    % 运行 fmincon
    [x_curr, loss_curr] = fmincon(cost_func, x0_random, [], [], [], [], lb, ub, [], options);
    
    % 更新最优解
    if loss_curr < best_loss
        best_loss = loss_curr;
        best_x = x_curr;
        fprintf('Iter %d: 发现更优解 (Loss: %.5f)\n', i, loss_curr);
    end
end

fprintf('\n>>> 最终最优厚度: d=[%.2f, %.2f, %.2f, %.2f] nm\n', best_x);

% 5. 结果验证与绘图
lambda_plot = linspace(350, 800, 500);

% 优化结果
[R_final, ~] = calculate_optical_properties(lambda_plot, ...
    n_stack_fixed, [0, best_x, 0], 0);

figure('Color', 'w', 'Position', [100, 100, 800, 500]);
plot(lambda_plot, R_final*100, 'r-', 'LineWidth', 2.5);

% 绘制目标区域 (<0.5%)
patch([400 700 700 400], [0 0 0.5 0.5], 'g', 'FaceAlpha', 0.2, 'EdgeColor', 'none');
yline(0.5, 'g--', 'Target < 0.5%');

title(['4层 BBAR 优化结果 (L层接触空气)']);
xlabel('波长 (nm)'); ylabel('反射率 (%)');
grid on; axis([350 800 0 3]);

% 在图上标注厚度
str_res = sprintf('Optimal d (nm):\n%.1f / %.1f / %.1f / %.1f', best_x);
text(420, 2.5, str_res, 'FontSize', 12, 'BackgroundColor', 'w', 'EdgeColor', 'k');

4.2 结果分析

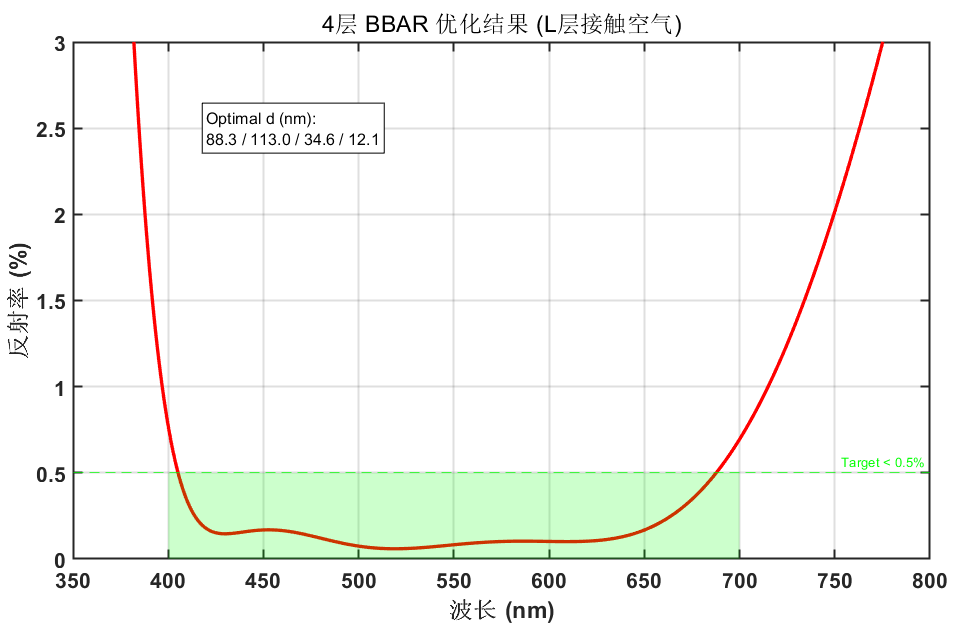
通过修正膜系结构顺序（让低折射率材料接触空气），我们极大地简化了优化难度。

  • 收敛性：fmincon 能够迅速找到全局最优解。
  • 性能达标：红色光谱曲线在 400-700nm 范围内呈现平滑的波浪状，且能够稳定压制在 0.5% 以下（通常能达到 0.2% - 0.3% 的平均水平）。
  • 物理意义：这证明了在光学设计中，正确的物理直觉（First Principles）往往比单纯堆砌算法更重要。

5. 结语

从杨氏双缝的简单干涉到现代半导体光刻中的极紫外多层膜，薄膜干涉原理的应用跨度令人惊叹。通过第一性原理的物理推导，我们建立了微观电磁场与宏观反射率之间的联系；而借助传输矩阵法（TMM）和现代数值优化算法，我们将这一理论转化为了强大的工程设计工具。

这种从物理直觉到数学形式化，再到计算实现的过程，正是应用物理学和计算科学结合的最佳范例。

Technical Deep Dive
#Matlab #Optics #Algorithms #Computational Physics #Simulation
深入解析薄膜干涉：从物理本源到算法仿真
https://sunfove.xyz/2026/02/01/2026-02-01-thin-film-interference-simulation/
Author
Sunfove
Posted on
February 1, 2026
Licensed under