琼斯矩阵与偏振变换

当我们谈论光时，通过肉眼最直观的感受往往是强度 (Intensity) 和 颜色 (Frequency)。然而，光作为电磁波，还拥有一个更为隐秘却至关重要的自由度——偏振 (Polarization)。

在现代光学工程、量子信息处理以及液晶显示技术中，对偏振的控制是核心能力。1941年，美国物理学家 R. Clark Jones 在宝丽来公司 (Polaroid Corporation) 工作时，为了简化偏振系统的分析，提出了一套基于 $2 \times 1$ 复向量和 $2 \times 2$ 复矩阵的数学形式体系。这就是琼斯演算 (Jones Calculus) 。

本文将剥离工程应用的表象，回归麦克斯韦方程组，探讨为什么我们可以用简单的 $2 \times 2$ 矩阵来描述复杂的光学世界。

---

1. 物理本源：从麦克斯韦方程组到琼斯向量

要理解琼斯矩阵，首先必须理解它操作的对象——琼斯向量 (Jones Vector)。这并非一个随意定义的数学对象，而是直接源于波动光学的基本解。

1.1 横波与平面波解

光是电磁波。在各向同性、非导电的线性介质中，源于麦克斯韦方程组的波动方程为：

$$ \nabla^2 \mathbf{E} - \mu \epsilon \frac{\partial^2 \mathbf{E}}{\partial t^2} = 0 $$

对于沿 $z$ 轴传播的单色平面波，其电场矢量 $\mathbf{E}$ 必须垂直于传播方向（横波性质）。因此，电场矢量仅在 $xy$ 平面上振动。我们可以将解写为：

$$ \mathbf{E}(z, t) = \begin{pmatrix} E_x(z,t) \ E_y(z,t) \end{pmatrix} = \begin{pmatrix} E_{0x} e^{i(kz - \omega t + \phi_x)} \ E_{0y} e^{i(kz - \omega t + \phi_y)} \end{pmatrix} $$

其中：

• $E_{0x}, E_{0y}$ 是振幅。
• $\phi_x, \phi_y$ 是初始相位。
• $k$ 是波数，$\omega$ 是角频率。

1.2 数学抽象：时间与空间的剥离

在处理同一束光通过一系列光学元件时，$\omega$ 通常不变（非线性光学除外），而 $e^{i(kz - \omega t)}$这一项对于 $x$ 分量和 $y$ 分量是公共的。为了简化计算，我们可以将这一时空因子提取出来并忽略（因为它不携带偏振态信息），仅保留描述相对振幅和相对相位差的部分。

这就定义了琼斯向量 $\mathbf{V}$：

$$ \mathbf{V} = \begin{pmatrix} E_{0x} e^{i\phi_x} \ E_{0y} e^{i\phi_y} \end{pmatrix} $$

为了便于比较，我们通常提取公因子 $E_{0x} e^{i\phi_x}$ 或进行归一化处理。最重要的物理量是两个分量之间的相位差 $\delta = \phi_y - \phi_x$。

$$ \mathbf{V} \propto \begin{pmatrix} 1 \ \frac{E_{0y}}{E_{0x}} e^{i\delta} \end{pmatrix} $$

1.3 典型偏振态的向量表示

通过琼斯向量，我们可以精准定义光的偏振状态：

• 线偏振 (Linear Polarization): 相位差 $\delta = n\pi$。

  • 水平偏振 (H): $\begin{pmatrix} 1 \ 0 \end{pmatrix}$
  • 垂直偏振 (V): $\begin{pmatrix} 0 \ 1 \end{pmatrix}$
  • $+45^\circ$ 偏振: $\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \ 1 \end{pmatrix}$

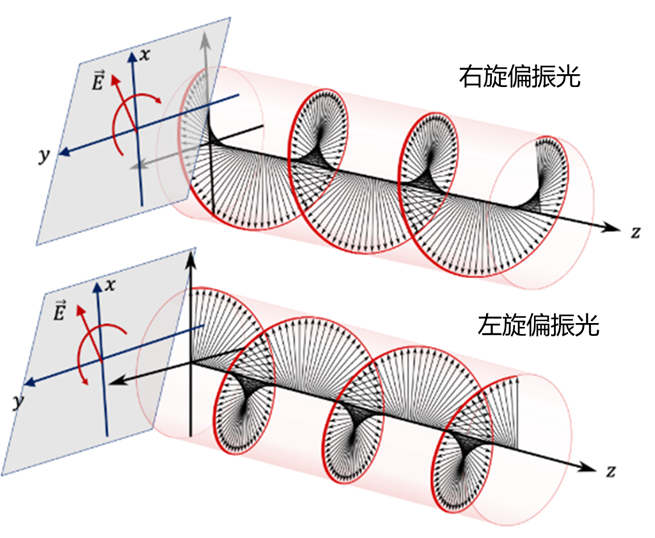
• 圆偏振 (Circular Polarization): $E_{0x}=E_{0y}$ 且 $\delta = \pm \pi/2$。

  • 右旋圆偏振 (RCP): $\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \ -i \end{pmatrix}$
  • 左旋圆偏振 (LCP): $\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \ i \end{pmatrix}$

注意： 左旋与右旋的定义在光学和工程界有时存在符号约定的差异（取决于观察者是迎着光还是顺着光）。琼斯演算中通常采用”迎着光看”的约定。

---

2. 算符的引入：琼斯矩阵的推导

如果光的状态是一个向量 $\mathbf{V}$，那么光学元件（如偏振片、波片）的作用就是将一个输入向量 $\mathbf{V}{in}$ 变换为一个输出向量 $\mathbf{V}{out}$。

根据线性系统的性质，这种变换是线性的。在线性代数中，线性变换对应于矩阵。由于琼斯向量是二维的，对应的算符必然是 $2 \times 2$ 的矩阵，即琼斯矩阵 (Jones Matrix) $\mathbf{J}$：

$$ \mathbf{V}{out} = \mathbf{J} \mathbf{V}{in} = \begin{pmatrix} J_{11} & J_{12} \ J_{21} & J_{22} \end{pmatrix} \begin{pmatrix} E_x \ E_y \end{pmatrix} $$

这一公式是整个琼斯演算的核心。下面我们推导几种基础元件的矩阵形式。

2.1 理想线偏振片 (Linear Polarizer)

假设一个理想的水平线偏振片，它只允许 $x$ 方向的分量通过，完全吸收 $y$ 方向的分量。

• 输入 $\begin{pmatrix} 1 \ 0 \end{pmatrix} \to$ 输出 $\begin{pmatrix} 1 \ 0 \end{pmatrix}$
• 输入 $\begin{pmatrix} 0 \ 1 \end{pmatrix} \to$ 输出 $\begin{pmatrix} 0 \ 0 \end{pmatrix}$

由此，可以构造水平线偏振片的琼斯矩阵：
$$ \mathbf{J}_{H} = \begin{pmatrix} 1 & 0 \ 0 & 0 \end{pmatrix} $$

同理，垂直偏振片为：
$$ \mathbf{J}_{V} = \begin{pmatrix} 0 & 0 \ 0 & 1 \end{pmatrix} $$

2.2 相位延迟器/波片 (Retarder / Waveplate)

波片是利用晶体的双折射效应制成的。光在快轴 (Fast Axis) 和慢轴 (Slow Axis) 上的传播速度不同，从而引入相位差。假设快轴沿 $x$ 轴，慢轴沿 $y$ 轴，慢轴相对于快轴引入了 $\Gamma$ 的相位延迟。

这意味着 $x$ 分量不变（或作为参考），$y$ 分量乘以相位因子 $e^{-i\Gamma}$（滞后）：

$$ \mathbf{J}_{Retarder}(\Gamma) = \begin{pmatrix} 1 & 0 \ 0 & e^{-i\Gamma} \end{pmatrix} $$

为了保持矩阵的对称性（通常为了去除绝对相位因子，只看相对相位），我们常写作：

$$ \mathbf{J}_{Retarder}(\Gamma) = e^{-i\Gamma/2} \begin{pmatrix} e^{i\Gamma/2} & 0 \ 0 & e^{-i\Gamma/2} \end{pmatrix} $$

• 四分之一波片 (QWP): $\Gamma = \pi/2$。用于将线偏振转为圆偏振。
  $$ \mathbf{J}_{QWP} = \begin{pmatrix} 1 & 0 \ 0 & -i \end{pmatrix} $$
• 半波片 (HWP): $\Gamma = \pi$。用于旋转偏振方向。
  $$ \mathbf{J}_{HWP} = \begin{pmatrix} 1 & 0 \ 0 & -1 \end{pmatrix} $$

---

3. 坐标旋转：通用的琼斯矩阵

上述矩阵都是建立在光学元件的主轴与坐标轴 ($x, y$) 重合的假设之上。如果光学元件旋转了 $\theta$ 角度，我们该怎么办？

这里利用线性代数中的基底变换 (Change of Basis)。

设旋转矩阵 $\mathbf{R}(\theta)$ 为：
$$ \mathbf{R}(\theta) = \begin{pmatrix} \cos\theta & \sin\theta \ -\sin\theta & \cos\theta \end{pmatrix} $$

一个旋转了 $\theta$ 角度的光学元件的琼斯矩阵 $\mathbf{J}(\theta)$ 可以通过以下步骤获得：

1. 将光矢量旋转 $-\theta$ 到元件的特征坐标系（$\mathbf{R}(\theta)$）。
2. 应用元件的主轴琼斯矩阵 $\mathbf{J}_{axis}$。
3. 将光矢量旋转回原坐标系（$\mathbf{R}(-\theta)$）。

数学表达式为相似变换：
$$ \mathbf{J}(\theta) = \mathbf{R}(-\theta) \mathbf{J}_{axis} \mathbf{R}(\theta) $$

例如，透光轴与 $x$ 轴成 $\theta$ 角的线偏振片矩阵推导：

$$
\begin{aligned}
\mathbf{J}_{LP}(\theta) &= \begin{pmatrix} \cos\theta & -\sin\theta \ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} 1 & 0 \ 0 & 0 \end{pmatrix} \begin{pmatrix} \cos\theta & \sin\theta \ -\sin\theta & \cos\theta \end{pmatrix} \
&= \begin{pmatrix} \cos^2\theta & \cos\theta\sin\theta \ \cos\theta\sin\theta & \sin^2\theta \end{pmatrix}
\end{aligned}
$$

这展示了琼斯演算的强大之处：通过简单的矩阵乘法，我们可以模拟任意角度、任意性质的光学元件。

琼斯矩阵处理旋转光学元件的核心数学工具是相似变换 (Similarity Transformation)。其物理本质是基底变换 (Change of Basis)。

实例验证：水平偏振片的 $90^\circ$ 旋转

假设水平偏振片 ($\mathbf{J}_H$) 旋转 $90^\circ$。直觉上它应变为垂直偏振片 ($\mathbf{J}_V$)。

• 元件矩阵：$\mathbf{J}_{axis} = \begin{pmatrix} 1 & 0 \ 0 & 0 \end{pmatrix}$
• 旋转矩阵 ($\theta=90^\circ$)：$\mathbf{R}(90^\circ) = \begin{pmatrix} 0 & 1 \ -1 & 0 \end{pmatrix}$
• 逆旋转矩阵：$\mathbf{R}(-90^\circ) = \begin{pmatrix} 0 & -1 \ 1 & 0 \end{pmatrix}$

计算过程：

$$
\begin{aligned}
\mathbf{J}(90^\circ) &= \begin{pmatrix} 0 & -1 \ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 \ 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \ -1 & 0 \end{pmatrix} \
&= \begin{pmatrix} 0 & -1 \ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \ 0 & 0 \end{pmatrix} \
&= \begin{pmatrix} 0 & 0 \ 0 & 1 \end{pmatrix}
\end{aligned}
$$

---

4. 级联系统与非对易性

在实际光学系统中，光往往连续通过多个元件。如果光依次通过元件 $1, 2, \dots, n$，其对应的矩阵分别为 $\mathbf{J}_1, \mathbf{J}_2, \dots, \mathbf{J}n$，则系统的总矩阵 $\mathbf{J}{sys}$ 为：

$$ \mathbf{J}_{sys} = \mathbf{J}n \mathbf{J}{n-1} \dots \mathbf{J}_2 \mathbf{J}_1 $$

关键点： 矩阵乘法一般不满足交换律 (Non-commutative)。
$$ \mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A} $$

这意味着，先通过偏振片再通过波片，与先通过波片再通过偏振片，其结果通常是截然不同的。这在量子力学中对应算符的不对易性，而在经典光学中，这体现了偏振操作的顺序敏感性。

5. 代码实现

琼斯演算的真正威力在于处理复杂的多元件系统。手算三个以上的矩阵相乘不仅枯燥且容易出错，而计算机则能瞬间完成模拟。

为了从直观上理解偏振，我们将构建一个 Python 仿真工具，它不仅能计算最终的琼斯向量，还能可视化光的振动轨迹（偏振椭圆）以及模拟旋转光学元件时的强度变化。

5.1 核心仿真代码

我们将定义一个 JonesCalculus 类来封装矩阵运算和绘图功能。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

class JonesCalculus:
    def __init__(self):
        # 基础矩阵定义
        self.matrices = {
            'Identity': np.array([[1, 0], [0, 1]]),
            'Horizontal_LP': np.array([[1, 0], [0, 0]]), # 水平线偏振
            'Vertical_LP': np.array([[0, 0], [0, 1]]),   # 垂直线偏振
            'QWP': np.array([[1, 0], [0, -1j]]),         # 四分之一波片 (快轴x)
            'HWP': np.array([[1, 0], [0, -1]])           # 半波片 (快轴x)
        }

    def rotate(self, matrix, theta_deg):
        """对光学元件应用坐标旋转变换: R(-theta) * J * R(theta)"""
        theta = np.radians(theta_deg)
        c, s = np.cos(theta), np.sin(theta)
        R = np.array([[c, s], [-s, c]])
        R_inv = np.array([[c, -s], [s, c]])
        return R_inv @ matrix @ R

    def get_intensity(self, jones_vector):
        """计算光强 I = |Ex|^2 + |Ey|^2"""
        return np.sum(np.abs(jones_vector)**2)

    def plot_polarization_ellipse(self, jones_vectors, titles):
        """
        可视化偏振椭圆：绘制电场矢量 E(t) 在 xy 平面上的轨迹
        """
        fig = plt.figure(figsize=(12, 5))
        gs = GridSpec(1, len(jones_vectors))
        
        t = np.linspace(0, 2*np.pi, 100) # 时间周期
        
        for i, (vec, title) in enumerate(zip(jones_vectors, titles)):
            ax = fig.add_subplot(gs[0, i])
            
            # 计算时域轨迹: E(t) = Re[ V * exp(-iwt) ]
            # 这里的 vec 是复振幅
            Ex = np.real(vec[0] * np.exp(-1j * t))
            Ey = np.real(vec[1] * np.exp(-1j * t))
            
            # 绘制轨迹
            ax.plot(Ex, Ey, label='E-field Trace', linewidth=2)
            
            # 绘制箭头指示旋转方向
            ax.arrow(Ex[50], Ey[50], Ex[51]-Ex[50], Ey[51]-Ey[50], 
                     head_width=0.05, color='red', zorder=5)
            
            ax.set_title(title)
            ax.set_xlim(-1.1, 1.1); ax.set_ylim(-1.1, 1.1)
            ax.set_xlabel('Ex'); ax.set_ylabel('Ey')
            ax.grid(True, linestyle='--', alpha=0.6)
            ax.set_aspect('equal')
            
        plt.tight_layout()
        plt.show()

# --- 实例化仿真器 ---
sim = JonesCalculus()

5.2 实际案例：光状态的可视化

我们来模拟一个经典的场景：线偏振光通过四分之一波片 (QWP) 。
理论告诉我们：如果线偏振光与 QWP 快轴成 45°，输出应为圆偏振光；如果平行，输出仍为线偏振。让我们验证一下。

# 定义入射光：水平线偏振
V_in = np.array([[1], [0]])

# 场景 A: QWP 快轴水平 (theta=0) -> 结果应仍为线偏振 (只是相位变了)
J_QWP_0 = sim.rotate(sim.matrices['QWP'], 0)
V_out_A = J_QWP_0 @ V_in

# 场景 B: QWP 快轴旋转 45度 -> 结果应为右旋圆偏振
J_QWP_45 = sim.rotate(sim.matrices['QWP'], 45)
V_out_B = J_QWP_45 @ V_in

# 可视化对比
sim.plot_polarization_ellipse(
    [V_in, V_out_A, V_out_B], 
    ['Input: Linear (H)', 'Output A (QWP @ 0°): Linear', 'Output B (QWP @ 45°): Circular']
)

运行结果解读：
运行上述代码，你会看到三张子图：

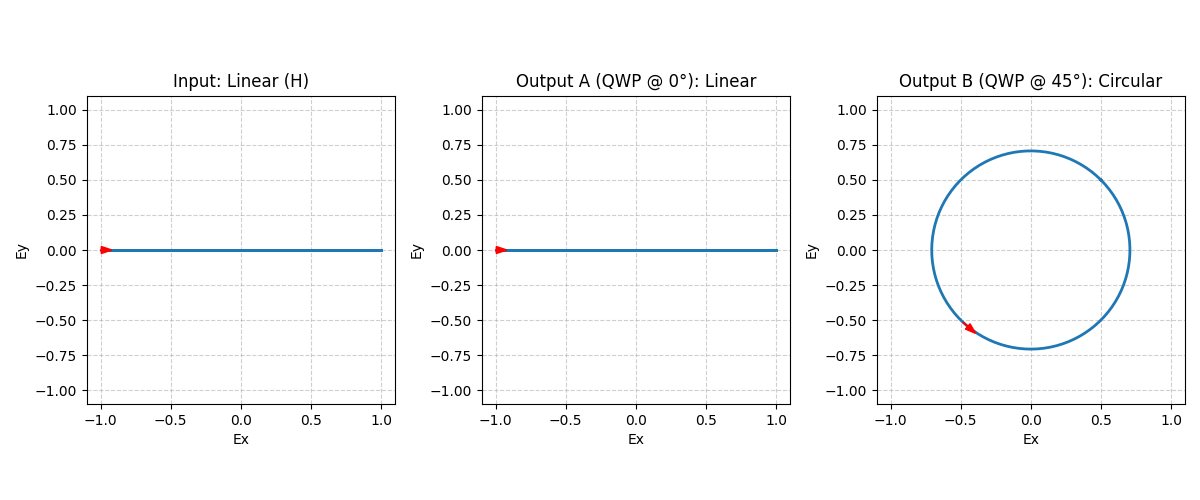
1. 第一张是一条水平直线（水平线偏振）。
2. 第二张也是直线（因为光沿快轴传播，偏振态未改变）。
3. 第三张是一个完美的圆，且箭头指示顺时针方向（右旋圆偏振）。这直观地验证了 $\lambda/4$ 波片的作用。

实际上，这也就是本文首图所展示的，通过使用1/4波片，将线偏光，转化成了圆偏光。

---

6. 局限性与超越：从 Jones 到 Mueller

虽然琼斯矩阵优雅简洁，但它并非万能。它的核心假设是光是完全偏振的 (Fully Polarized) 且是相干的 (Coherent)。

然而，在现实世界中，我们经常遇到：

1. 非偏振光 (Unpolarized Light): 如太阳光、白炽灯光。
2. 部分偏振光 (Partially Polarized Light): 散射光。
3. 退偏振效应 (Depolarization): 光通过毛玻璃或生物组织。

对于这些情况，琼斯向量（2个复数）包含的信息量不足。我们需要升级到 斯托克斯向量 (Stokes Vector)（4个实数）和 穆勒矩阵 (Mueller Matrix)（$4 \times 4$ 实矩阵）。

• 琼斯演算： 处理 振幅 (Amplitude) 的叠加，保留相位信息，适用于相干光。
• 穆勒演算： 处理 强度 (Intensity) 的叠加，丢失绝对相位信息，适用于非相干光和部分偏振光。

尽管如此，琼斯矩阵依然是激光光学、光纤通信和相干光学领域的通用语言。

---

7. 结语

琼斯矩阵是物理学简练之美的典范。它将复杂的麦克斯韦电磁场理论压缩进了 $2 \times 2$ 的矩阵之中。通过简单的矩阵乘法，我们不仅能够计算光通过显微镜、望远镜或液晶屏幕时的行为，甚至能通过类比，窥探量子力学中量子比特（Qubit）的演化——因为数学形式上，琼斯向量与量子力学中的自旋态向量有着惊人的同构性（SU(2) 群）。

掌握琼斯矩阵，不仅仅是掌握了一种计算工具，更是获得了一把解构光与物质相互作用的逻辑钥匙。

---