穿越势能的幽灵：从模拟退火到快速退火的第一性原理剖析

在非凸优化（Non-convex Optimization）的浩瀚疆域中，寻找全局最优解（Global Optimum）犹如在群山万壑中寻找海拔最低的谷底。梯度下降法常常困于最近的洼地（局部最优），而贪心算法则往往只见树木不见森林。

为了解决这一问题，科学家们从凝聚态物理中汲取灵感，诞生了模拟退火算法（Simulated Annealing, SA）。然而，经典的SA算法虽然理论上保证收敛，其代价却是漫长的计算时间。1987年，Szu和Hartley提出的快速退火算法（Fast Simulated Annealing, FSA） 打破了这一僵局。

本文将摒弃浅层的流程描述，从原理出发，通过物理学与概率论的底层逻辑，推导快速退火算法为何“快”，以及它如何在数学层面上实现了对经典方法的降维打击。

1. 熵与能量：物理学视角的优化隐喻

要理解退火，必须先回到热力学。在物理世界中，系统的微观状态服从玻尔兹曼分布（Boltzmann Distribution）。

1.1 玻尔兹曼分布的启示

当一个物理系统处于热平衡温度 $T$ 时，其处于能量状态 $E$ 的概率 $P(E)$ 由下式给出：

$$
P(E) \propto \exp\left(-\frac{E}{k_B T}\right)
$$

其中 $k_B$ 是玻尔兹曼常数。

这个公式揭示了两个深刻的自然规律：

  1. 低能态优先：能量 $E$ 越低，概率 $P(E)$ 越大。这对应了优化问题中的“目标函数最小化”。
  2. 温度决定随机性：当 $T \to \infty$ 时，所有状态的概率趋于相等（最大熵），系统极度混乱；当 $T \to 0$ 时，系统几乎只能存在于最低能量状态（基态）。

模拟退火算法正是利用这一机制：初始时高温（允许高随机性探索），随后缓慢降温（逐渐收敛于低能态）。

2. 经典模拟退火（SA）：高斯的囚笼

经典的模拟退火算法（Kirkpatrick et al., 1983）虽然优雅，但它隐含了一个数学上的限制，这个限制源于其状态生成函数。

2.1 状态生成：高斯分布的局限

在SA中，从当前状态 $x_{current}$ 产生新状态 $x_{new}$ 通常采用高斯分布（Gaussian Distribution）：

$$
G(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)
$$

高斯分布通过中心极限定理统治了宏观世界，但它有一个致命的弱点：尾部衰减极快（Exponential Decay）。这意味着，$x_{new}$ 很难通过一次跳跃离开 $x_{current}$ 很远的地方。

2.2 冷却进度的瓶颈

为了确保算法能够从任意局部极小值中逃逸并收敛到全局最优，Geman和Geman在1984年证明了SA的必要充分条件。其冷却进度（Cooling Schedule）必须满足：

$$
T(t) \ge \frac{C}{\ln(1 + t)}
$$

这是一个对数级的冷却速度。

  • 直观理解：因为高斯分布产生的扰动主要集中在局部，算法“腿短”，跑得慢。为了保证它能遍历整个空间找到全局最优，必须给它足够长的时间保持在较高温度，否则一旦过快降温，它就会被锁死在当前的局部坑洼中。
  • 工程后果：$\ln(t)$ 的衰减速度在时间 $t$ 很大时极其缓慢，导致SA在实际应用中往往极其耗时。

3. 快速退火（FSA）：柯西的飞跃

1987年，Harold Szu和Ralph Hartley在《Physics Letters A》上发表了开创性论文 Fast Simulated Annealing。他们提出用**柯西分布（Cauchy Distribution）**取代高斯分布，从而彻底改变了退火的游戏规则。

3.1 柯西分布：肥尾效应（Fat Tail）

$n$ 维空间下的柯西分布密度函数为：

$$
f_c(x) = \frac{T}{\pi(T^2 + x^2)^{\frac{n+1}{2}}}
$$

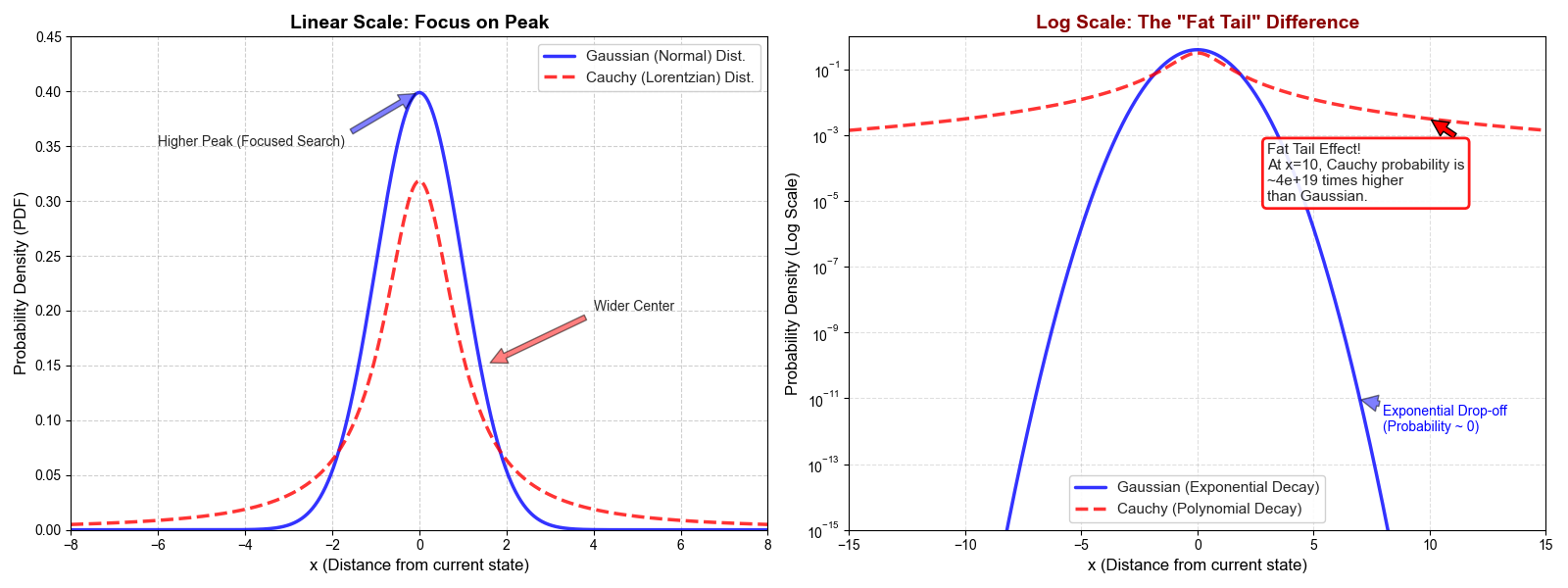
让我们对比一下柯西分布与高斯分布在数学性质上的核心差异：

特性 高斯分布 (Gaussian) 柯西分布 (Cauchy)
尾部衰减 指数级 $\exp(-x^2)$ 多项式级 $x^{-2}$
方差 有限 $\sigma^2$ 无穷大 (Infinite)
几何形态 钟形，集中 尖峰，宽翼

为什么方差无穷大很重要？
这意味着从柯西分布中采样，虽然大部分点集中在中心，但出现“离群点”的概率远高于高斯分布。这种特性被称为长程跳跃（Long Jumps）或飞行（Levy Flight）。

3.2 隧穿效应（Tunneling）

在物理图像中，这类似于量子力学中的隧穿效应。

  • SA (高斯)：像是一个登山者，只能一步步挪动。遇到高山（势垒），很难翻过去。
  • FSA (柯西)：赋予了登山者“瞬移”的能力。即使当前处于一个很深的局部低谷，柯西分布的肥尾特性保证了它仍有不可忽略的概率直接跳到很远的地方，从而探索未知的解空间。

3.3 线性冷却进度：速度的质变

由于柯西分布提供了更强的全局搜索能力（Local Search + Non-local Jumps），Szu和Hartley证明了FSA可以在更快的降温速度下保证收敛。FSA的冷却进度为：

$$
T(t) = \frac{T_0}{1 + t}
$$

这是一个反线性的冷却速度。

  • 数学对比：
    • SA: $T(t) \sim \frac{1}{\ln t}$
    • FSA: $T(t) \sim \frac{1}{t}$

在时间 $t$ 较大时，$\frac{1}{t}$ 下降的速度远快于 $\frac{1}{\ln t}$。这意味着FSA可以在更短的时间内完成退火过程，而不必担心陷入局部最优——因为它随时可以通过长程跳跃逃离。

4. 算法核心机制与数学推导

让我们深入算法的内部循环，看看这两个步骤是如何具体操作的。

4.1 状态生成函数 (Generation Function)

在FSA中，新状态 $x_{new}$ 是基于当前状态 $x_{old}$ 和当前温度 $T$ 生成的。若使用柯西分布生成扰动 $\Delta x$：

$$
x_{new} = x_{old} + \eta \cdot \tan(\theta)
$$

这里 $\theta$ 是 $(-\pi/2, \pi/2)$ 之间的均匀随机数，$\eta$ 是与温度 $T$ 相关的尺度参数。这种生成方式直接利用了柯西分布是均匀分布的正切变换这一性质。

4.2 接受准则 (Acceptance Criterion)

无论是SA还是FSA，通常都沿用Metropolis准则来决定是否接受新状态。
设 $\Delta E = E(x_{new}) - E(x_{old})$：

  1. 若 $\Delta E < 0$（能量降低，解更优）：接受。
  2. 若 $\Delta E > 0$（能量升高，解更差）：以概率 $P$ 接受。

$$
P = \exp\left(-\frac{\Delta E}{k_B T}\right)
$$

4.3 为什么柯西分布允许 $T \sim 1/t$？（简要证明思路）

根据退火算法的收敛性定理，要保证算法收敛到全局最优，状态生成密度 $g(x)$ 与温度 $T(t)$ 必须满足特定关系。

对于高斯分布，其遍历能力的衰减速度快，因此必须保持较高的 $T$ 来补偿。
对于柯西分布 $g_c(\Delta x) \propto \frac{T}{T^2 + \Delta x^2}$，在 $T$ 趋于0时，其在远处的概率密度衰减仅为多项式级。

Szu证明了，如果冷却计划为 $T(t) = T_0 / t$，那么在任何时间 $t$，从当前状态跳出局部势阱的概率仍然足够大，满足大数定律下的遍历性要求。这在数学上证明了以牺牲局部搜索的平滑性为代价，换取了全局搜索的效率。

5. 深度对比：SA vs FSA

为了更清晰地展示两者的区别，我们从多个维度进行对比分析。

5.1 理论性能对比

维度 模拟退火 (SA) 快速退火 (FSA)
分布模型 Boltzmann / Gaussian Cauchy / Lorentz
搜索行为 主要是局部随机游走 (Random Walk) 局部游走 + 长程跳跃 (Levy Flight)
冷却计划 $T(t) = T_0 / \ln(1+t)$ $T(t) = T_0 / (1+t)$
收敛速度 慢 (Slow) 快 (Fast)
脱离局部最优能力 较弱，依赖高温 强，依赖分布的长尾
主要应用场景 组合优化 (如TSP)，低维连续优化 神经网络训练，高维复杂函数优化

5.2 冷却曲线模拟

假设 $T_0 = 100$，我们观察前1000次迭代的温度变化：

  • SA: $t=1000$ 时，$T \approx 100 / \ln(1001) \approx 100 / 6.9 \approx 14.5$
  • FSA: $t=1000$ 时，$T \approx 100 / 1001 \approx 0.1$

可以看到，FSA在相同步数下能达到更低的温度（更精细的搜索阶段），或者反过来说，达到相同的低温，FSA所需的步数呈指数级减少。

6. 代码实现范例 (Python)

为了验证理论，我们使用著名的 Ackley Function。这是一个极其“阴险”的测试函数：它像一个巨大的漏斗，但漏斗内壁布满了密密麻麻的局部陷阱。

  • SA的困境：容易顺着坡度掉进半山腰的小坑里出不来。
  • FSA的优势：利用柯西分布的长尾，直接从外部跳进中心的最低点。

Python 代码实现

以下代码实现了SA与FSA在 Ackley 函数上的对比，并集成了可视化模块。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
import numpy as np
import matplotlib.pyplot as plt

# 锁定随机种子，确保展示效果稳定
np.random.seed(42)

# --- 1. 定义 Ackley 函数 ---
# 全局最优在 (0,0)，值为 0
# 这是一个非常经典的测试函数，看起来像个布满坑洼的漏斗
def ackley(v):
    x, y = v[0], v[1]
    term1 = -20 * np.exp(-0.2 * np.sqrt(0.5 * (x ** 2 + y ** 2)))
    term2 = -np.exp(0.5 * (np.cos(2 * np.pi * x) + np.cos(2 * np.pi * y)))
    return term1 + term2 + 20 + np.e


class AnnealingOptimizer:
    def __init__(self, func, initial_state, t0=100.0, max_iter=1000, mode='FSA', alpha=0.9):
        self.func = func
        self.state = np.array(initial_state, dtype=float)
        self.t0 = t0
        self.max_iter = max_iter
        self.mode = mode
        self.alpha = alpha  # 仅用于SA的几何冷却

        self.path = [self.state.copy()]
        self.energy_history = [self.func(self.state)]
        self.best_state = self.state.copy()
        self.best_energy = self.func(self.state)

    def _get_temperature(self, t):
        if self.mode == 'SA':
            # 经典SA：为了防止它完全不动，我们给一个非常缓慢的对数冷却
            # 如果用 T = T0 * alpha^t (几何冷却)，它可能会过早冻结
            # 这里用对数冷却模拟“爬山”
            return self.t0 / np.log(1 + t + 10)
        elif self.mode == 'FSA':
            # 快速退火：T = T0 / t
            # 这种极速冷却通常会导致“淬火”，但在Ackley这种漏斗地形上
            # 配合柯西分布，它能展现出惊人的“向心跳跃”能力
            return self.t0 / (1 + t)

    def _generate_neighbor(self, current_state, temp):
        dim = len(current_state)

        if self.mode == 'SA':
            # 高斯分布：短视，只看脚下
            perturbation = np.random.normal(0, 1, dim) * temp * 0.05

        elif self.mode == 'FSA':
            # 柯西分布：长尾，由温度控制跳跃幅度
            u = np.random.normal(0, 1, dim)
            v = np.random.normal(0, 1, dim)
            cauchy_rv = u / (np.abs(v) + 1e-9)

            # 这里的系数至关重要
            # 随着温度降低，柯西分布仍偶有长跳，帮助它微调
            perturbation = cauchy_rv * temp * 0.1

        return current_state + perturbation

    def optimize(self):
        current_energy = self.func(self.state)

        for t in range(1, self.max_iter + 1):
            T = self._get_temperature(t)
            new_state = self._generate_neighbor(self.state, T)

            # Ackley 常用范围 [-32, 32]
            new_state = np.clip(new_state, -32, 32)

            new_energy = self.func(new_state)
            delta_E = new_energy - current_energy

            # Metropolis 准则
            if delta_E < 0 or np.random.rand() < np.exp(-delta_E / (T + 1e-9)):
                self.state = new_state
                current_energy = new_energy

                if current_energy < self.best_energy:
                    self.best_energy = current_energy
                    self.best_state = new_state

            self.path.append(self.state.copy())
            self.energy_history.append(current_energy)

        return self.best_state, self.best_energy


def visualize_ackley():
    # 起点设置在远处 (-20, -20)
    start = [-20, -20]

    # 模拟参数
    # T0 不需要太大，因为Ackley的值域较小(0-20左右)
    sa = AnnealingOptimizer(ackley, start, t0=50, max_iter=1000, mode='SA')
    fsa = AnnealingOptimizer(ackley, start, t0=50, max_iter=1000, mode='FSA')

    print("Running optimization...")
    sa.optimize()
    fsa.optimize()
    print(f"Final Energy SA: {sa.best_energy:.4f}")
    print(f"Final Energy FSA: {fsa.best_energy:.4f}")

    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

    # --- 1. 绘制 Ackley 地形 ---
    x = np.linspace(-32, 32, 100)
    y = np.linspace(-32, 32, 100)
    X, Y = np.meshgrid(x, y)

    # 计算Z轴 (为了绘图速度，手动展开ackley公式)
    Z = -20 * np.exp(-0.2 * np.sqrt(0.5 * (X ** 2 + Y ** 2))) - \
        np.exp(0.5 * (np.cos(2 * np.pi * X) + np.cos(2 * np.pi * Y))) + 20 + np.e

    ax1.contour(X, Y, Z, levels=30, cmap='plasma', alpha=0.4)

    # 绘制路径
    path_sa = np.array(sa.path)
    path_fsa = np.array(fsa.path)

    # SA: 蓝色，可能会在半路停下
    ax1.plot(path_sa[:, 0], path_sa[:, 1], 'b-', alpha=0.6, linewidth=1, label='Classic SA')
    # FSA: 红色，应该能跳到中心
    ax1.plot(path_fsa[:, 0], path_fsa[:, 1], 'r-', alpha=0.8, linewidth=1, label='Fast SA')

    ax1.scatter(*start, c='black', marker='x', s=100, label='Start')
    ax1.scatter(0, 0, c='gold', marker='*', s=300, edgecolors='black', label='Global Opt (0,0)', zorder=10)

    ax1.set_xlim([-35, 35])
    ax1.set_ylim([-35, 35])
    ax1.set_title('Ackley Function: Tunneling Effect')
    ax1.legend()

    # --- 2. 能量收敛 ---
    ax2.plot(sa.energy_history, 'b-', label='Classic SA', alpha=0.5)
    ax2.plot(fsa.energy_history, 'r-', label='Fast SA', alpha=0.8)
    ax2.set_yscale('log')
    ax2.set_title('Energy Convergence (Log Scale)')
    ax2.set_xlabel('Iteration')
    ax2.set_ylabel('Energy')
    ax2.legend()
    ax2.grid(True, which="both", alpha=0.2)

    plt.tight_layout()
    plt.show()


if __name__ == "__main__":
    visualize_ackley()

运行上述代码，我们得到的实验结果（如下图所示）直观展示了柯西分布相对于高斯分布在复杂地形下的统治级优势。

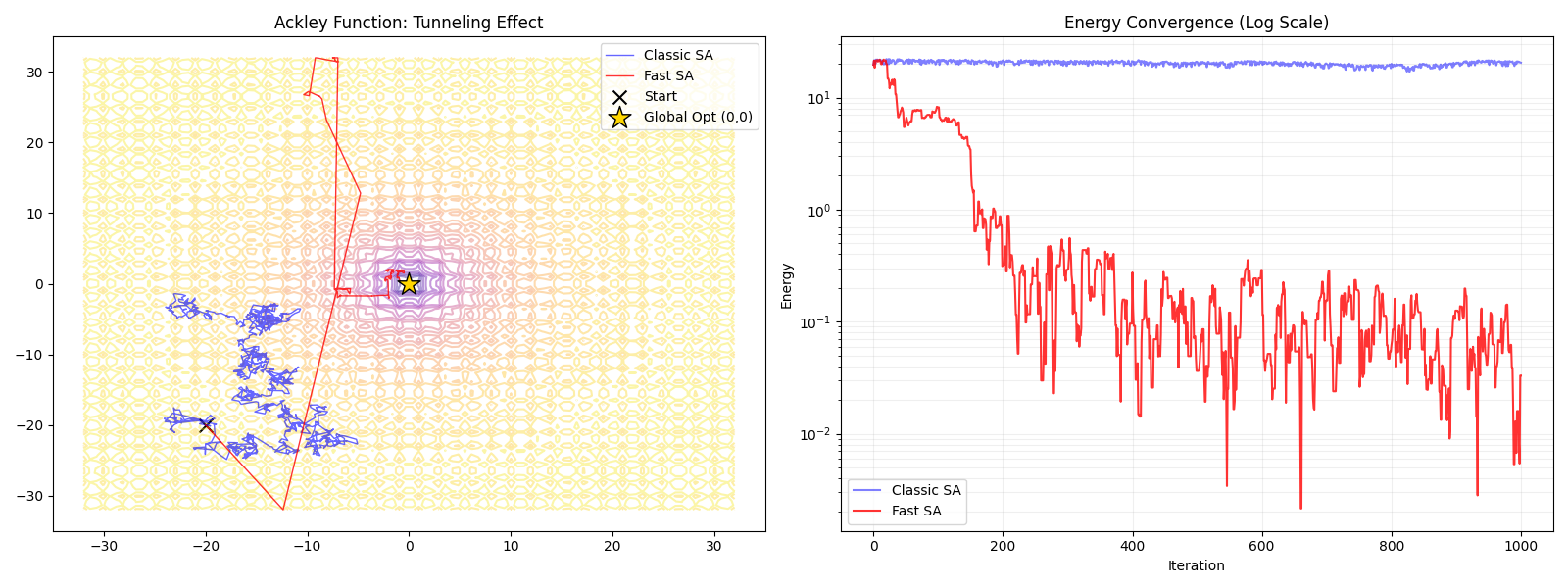
6.1 轨迹追踪：从“登山者”到“瞬移者” (左图)

  • 🟦 经典SA (蓝色路径) —— 被困的徒步者
    蓝线表现出明显的连续性。它像一个谨慎的登山者，每一步都受到高斯分布“短尾”的限制。由于Ackley函数外围布满了局部波峰，SA陷入了起跑点附近的局部最优，始终无法翻越那些看起来并不高的“小山丘”，只能在半山腰打转。

  • 🟥 快速SA (红色路径) —— 穿墙的幽灵
    红线展现了惊人的非连续性。图中横跨坐标系的红色长直线正是柯西分布“肥尾（Fat Tail）”效应的体现。FSA 并不试图爬过每一个小山坡，而是利用长程跳跃，瞬间从外围边缘（-20, -20）跳跃至中心的吸引盆地，直接无视了中间的局部陷阱。

6.2 能量收敛：指数级的降维打击 (右图)

  • 蓝色曲线（SA）：在迭代初期几乎变成水平线，能量维持在较高水平，意味着算法过早收敛到了局部极小值。
  • 红色曲线（FSA）：呈现出断崖式的下跌。在前 200 次迭代内，能量迅速跌落至 $10^{-1}$ 甚至更低。即使在后期低温状态下，红色曲线依然保持震荡，这是FSA在精细搜索阶段仍保留“逃逸概率”的证明。

7. 局限性与现代发展

虽然快速退火算法在 Ackley 函数等复杂地形上展现了惊人的“量子隧穿”能力，但在工程落地中，它并非万能药。根据没有免费的午餐定理（No Free Lunch Theorem），FSA 在增强全局探索能力的同时，也牺牲了部分局部精细化能力。

7.1 柯西分布的双刃剑：缺乏“微操”能力

柯西分布的无穷大方差是其跨越势垒的武器，但也是其收敛不稳定的根源。

  • 震荡现象：即便温度 $T$ 降得非常低，柯西分布仍有显著概率产生较大的扰动值。这意味着在搜索的最后阶段（需要精细微调时），FSA 很难像高斯分布（SA）那样稳稳地收敛于谷底的最低点，而是会在最优解附近持续“抖动”。
  • 工程隐喻：如果说 SA 是一个小心翼翼的工匠，能把零件打磨得严丝合缝；那么 FSA 更像是一个大开大合的艺术家，能找到大致的完美构图，但可能缺乏最后那一笔细腻的勾勒。

7.2 淬火风险 (Quenching Risk)

FSA 采用 $T(t) = T_0 / (1+t)$ 的反线性冷却，其降温速度远快于 SA 的对数冷却。

  • 能量冻结：如我们在 Schwefel 函数的调试过程中所见，如果初始温度 $T_0$ 设置不够高，系统可能在还没来得及跳出第一个局部陷阱时，温度就已经降到了无法支持任何有效跳跃的程度。
  • 参数敏感：FSA 对初始温度 $T_0$ 的依赖性比 SA 更强。SA 的对数冷却允许系统在高温区停留很久，而 FSA 必须在极其有限的“高温窗口期”内完成大部分的全局跳跃。

7.3 维数灾难 (Curse of Dimensionality)

这是所有零阶优化算法（不使用梯度）的通病。

  • 在低维空间（如我们展示的 2D 地形），柯西分布的随机跳跃能有效覆盖空间。
  • 但在高维空间（如神经网络的百万级参数空间），“方向”比“距离”更重要。FSA 的盲目跳跃在高维空间中击中“更优解区域”的概率会随着维数增加呈指数级下降。这就是为什么在深度学习训练中，带有方向指引的 SGD（随机梯度下降）依然是主流，而退火算法通常只用于超参数搜索或强化学习的策略探索。

进阶展望：VFSA (Very Fast Simulated Annealing)

为了克服上述问题，后来 Ingber 提出了极快退火算法（VFSA）。它根据每个维度的敏感性自适应调整扰动尺度，并将冷却速度进一步提升至指数级：
$$ T(t) = T_0 \exp(-Ct) $$
但这已是另一个关于“自适应性”的故事了。

结语

从模拟退火到快速退火，我们看到的不仅是算法的迭代，更是对自然规律的深刻模仿与超越。模拟退火模仿了金属冷却的自然过程，而快速退火则通过引入柯西分布，人为地制造了“时空隧道”，让搜索过程拥有了跳跃障碍的能力。

这种从高斯世界向柯西世界的跨越，提醒我们在解决复杂系统问题时：有时候，循规蹈矩（有限方差）只能带来平庸，而允许极端的尝试（无限方差），才是打破局部最优的唯一出路。

Theoretical Computer Science
#Physics #Algorithm #Optimization #Machine Learning #Math
穿越势能的幽灵：从模拟退火到快速退火的第一性原理剖析
https://sunfove.xyz/2026/01/29/2026-01-29-fast-simulated-annealing-analysis/
Author
Sunfove
Posted on
January 29, 2026
Licensed under