透视光影的边界：从第一性原理深度解析焦深与景深

在光学成像的世界里，“清晰”从来不是一个绝对的二元概念，而是一个关于“容忍度”的连续函数。当我们凝视一张照片或通过显微镜观察细胞时，我们所感知的清晰范围，实际上是光学系统对误差的某种妥协。

这种妥协在物方空间（Object Space）表现为景深（Depth of Field, DOF），而在像方空间（Image Space）则表现为焦深（Depth of Focus, DoFocus）。尽管这两个术语在日常摄影中常被混淆，但在光学工程、机器视觉以及半导体光刻领域，严格区分二者是理解成像系统极限的关键。

本文将摒弃经验法则，回归几何光学，通过数学推导揭示这两个概念的本质联系。

1. 定义：清晰度的物理边界

要讨论焦深和景深，首先必须引入一个核心概念：允许弥散圆（Circle of Confusion, CoC）。

在理想的高斯光学（Gaussian Optics）中，一个点光源应当汇聚成一个几何点。然而，受限于光的衍射极限（Diffraction Limit）和像差，以及成像介质（胶片颗粒或CCD/CMOS像素）的分辨率限制，真正的“点”是不存在的。

当一个光斑的直径小于人眼或传感器的分辨极限时，我们主观上认为它是“清晰”的。这个临界直径，就是允许弥散圆直径，通常记为 $c$。

1.1 焦深 (Depth of Focus)

焦深是指在保持物距不变的情况下，像平面（如胶片或传感器）沿光轴前后移动，而像点模糊程度仍保持在允许弥散圆内的移动范围。

物理本质：像方空间的轴向容差。
关键场景：相机装配精度、显微镜调焦、光刻机硅片平整度要求。

1.2 景深 (Depth of Field)

景深是指在像平面（焦平面）位置固定的前提下，被摄物体在沿光轴方向前后移动时，其在像平面上成的像仍能保持清晰的距离范围。

物理本质：物方空间的轴向容差。
关键场景：人像摄影（虚化背景）、风景摄影（超焦距）、机器视觉检测。

2. 焦深和景深的推导

2.1 基础定义与符号系统

在开始推导前，必须建立严格的符号系统（遵循高斯光学符号惯例）：

$f$：镜头焦距。
$D$：入瞳直径（光圈孔径）。
$N$：光圈数（F-Number），定义为 $N = f/D$。
$c$：允许弥散圆直径（Circle of Confusion, CoC）。
$u$：对焦平面的物距（Object Distance）。
$v$：对焦平面的像距（Image Distance）。
$m$：横向放大率（Magnification），$m = v/u$。

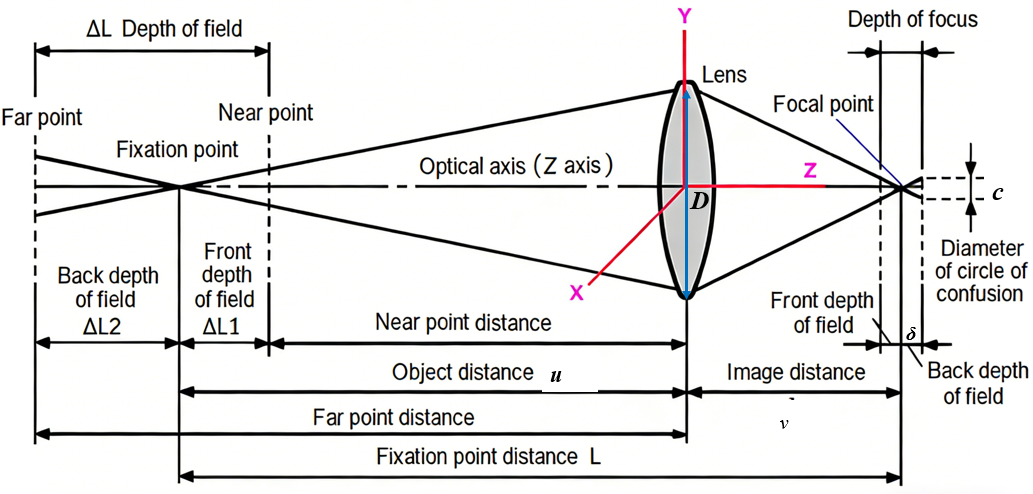
2.2 焦深 (Depth of Focus) 的严格推导

焦深描述的是像方空间的容差。假设像平面从理想焦平面移动了距离 $\delta$，使得原本汇聚成一点的光锥在像平面上形成了一个直径为 $c$ 的光斑。

2.2.1 几何构建

光线从透镜后方射出，形成一个底面直径为 $D$（出瞳直径，在此简化为等于入瞳直径），高为 $v$ 的圆锥体。

当像平面移动 $\delta$ 距离时，根据相似三角形原理（Thales Theorem）：

$$
\frac{c}{\delta} = \frac{D}{v}
$$

2.2.2 严格推导 (Exact Derivation)

从上述几何关系，我们可以直接解出单侧焦深 $\delta$：

$$
\delta = \frac{c \cdot v}{D}
$$

利用光圈数定义 $D = f/N$，代入上式：

$$
\delta = \frac{c \cdot v \cdot N}{f}
$$

引入放大率公式 $m = v/u$，结合高斯成像公式 $1/u + 1/v = 1/f$，我们可以推导出 $v = f(1+m)$。将其代入 $\delta$ 的表达式：

$$
\delta = \frac{c \cdot f(1+m) \cdot N}{f} = N \cdot c \cdot (1 + m)
$$

因此，严格的总焦深 $t$（包含前后两侧）为：

$$
t_{\text{exact}} = 2 \cdot \delta = 2 \cdot N \cdot c \cdot (1 + m)
$$

物理意义：此公式表明，焦深不仅取决于光圈 $N$ 和弥散圆 $c$，还与放大率 $m$ 线性相关。在微距摄影（$m$ 较大）中，焦深会显著增加。

2.2.3 近似推导 (Approximation)

在普通摄影场景中，物距通常远大于焦距（$u \gg f$），此时放大率 $m = v/u \approx 0$。像距 $v$ 无限接近于焦距 $f$。

忽略 $m$ 项，我们得到工程上最常用的近似公式：

$$
t_{\text{approx}} = 2 \cdot N \cdot c
$$

2.3 景深 (Depth of Field) 的严格推导

景深的推导涉及物象共轭关系的非线性变换，比焦深复杂得多。

2.3.1 几何构建与前置条件

设对焦在距离 $u$ 处，此时像距为 $v$。

近景深界限 $u_n$：物体移近到 $u_n$，其像点退后到 $v + \delta$，在原像平面 $v$ 处形成直径为 $c$ 的弥散圆。
远景深界限 $u_f$：物体移远到 $u_f$，其像点前移到 $v - \delta$，在原像平面 $v$ 处形成直径为 $c$ 的弥散圆。

根据像方几何关系（参考焦深推导），允许的像距偏移量 $\delta$ 为：
$$
\delta = \frac{c \cdot v}{D}
$$

2.3.2 严格推导 (Exact Derivation)

我们需要求解满足像距为 $v’ = v + \delta$ 的物距 $u_n$。根据高斯公式：

$$
u_n = \frac{f \cdot v’}{v’ - f} = \frac{f(v + \delta)}{v + \delta - f}
$$

将 $\delta = cv/D$ 代入：

$$
u_n = \frac{f(v + \frac{cv}{D})}{v + \frac{cv}{D} - f}
$$

这是一个极其繁琐的代数式。为了简化，我们引入超焦距 $H$ 的严格定义。
当对焦在无穷远时，$v=f$，此时像平面上的模糊斑直径由 $D$ 和 $f$ 决定。令无穷远物体的像斑刚好为 $c$，对应的最近清晰距离为 $H$。

严格的超焦距公式为：
$$
H = \frac{f^2}{N \cdot c} + f
$$
(注：绝大多数教材忽略末尾的 $+f$，但在严格推导中我们将保留它或在最后一步省略)

经过繁琐的代数变换（利用 $1/u + 1/v = 1/f$ 消除 $v$），我们可以得到严格的景深界限公式：

$$
u_n = \frac{u \cdot H_{\text{approx}}}{H_{\text{approx}} + (u - f)}
$$
$$
u_f = \frac{u \cdot H_{\text{approx}}}{H_{\text{approx}} - (u - f)}
$$

其中 $H_{\text{approx}} = f^2 / (Nc)$。

严格的总景深 $\Delta L$：

$$
\Delta L_{\text{exact}} = u_f - u_n = \frac{2 u (u-f) H_{\text{approx}}}{H_{\text{approx}}^2 - (u-f)^2}
$$

将 $H_{\text{approx}}$ 展开，得到完全展开式：

$$
\Delta L_{\text{exact}} = \frac{2 \cdot u \cdot (u-f) \cdot f^2 \cdot N \cdot c}{f^4 - (u-f)^2 \cdot N^2 \cdot c^2}
$$

2.3.3 近似推导 (Approximation)

上述公式在工程应用中过于复杂。我们进行三级近似：

近似条件 1：$u \gg f$（非微距摄影）。
此时 $(u-f) \approx u$。

近似条件 2：$H \gg u$（对焦距离远小于超焦距）。
这意味着分母中 $H^2$ 远大于 $(u-f)^2$，可以忽略减数项。

基于这两个条件，公式简化为：

$$
\Delta L \approx \frac{2 u \cdot u \cdot H}{H^2} = \frac{2 u^2}{H}
$$

代入 $H \approx f^2 / (Nc)$：

$$
\Delta L_{\text{approx}} = \frac{2 u^2 N c}{f^2}
$$

这就是我们在摄影教材中见到的经典公式。

2.4 总结与对比表

为了清晰展示严格解与近似解的区别，我们将其总结如下：

参数	严格公式 (Exact Formula)	近似公式 (Approximation)	适用条件
焦深 (DoFocus)	$$t = 2Nc(1+m)$$	$$t = 2Nc$$	普通摄影 ($m \approx 0$)
超焦距 ($H$)	$$H = \frac{f^2}{Nc} + f$$	$$H = \frac{f^2}{Nc}$$	长焦或大光圈 ($f^2/Nc \gg f$)
近景深 ($u_n$)	$$\frac{u H}{H + (u-f)}$$	$$\frac{u H}{H + u}$$	物距远大于焦距 ($u \gg f$)
远景深 ($u_f$)	$$\frac{u H}{H - (u-f)}$$	$$\frac{u H}{H - u}$$	物距远大于焦距 ($u \gg f$)
总景深 (DoF)	$$\frac{2 u (u-f) H}{H^2 - (u-f)^2}$$	$$\frac{2 u^2 N c}{f^2}$$	$u \gg f$ 且 $u \ll H$

2.5 什么时候必须使用严格公式？

微距摄影 (Macro Photography)：当放大率 $m > 0.1$ 时，近似公式误差呈指数级上升。此时焦深必须考虑 $(1+m)$ 项，否则会导致对焦行程估算严重不足。
显微镜设计：在显微光学中，$m \gg 1$，此时近似公式完全失效。
大画幅相机：由于焦距 $f$ 较长，且经常使用小光圈，严格计算超焦距中的 $+f$ 项有时也是必要的修正。

2.6焦深与景深影响因素

在光学工程与摄影实践中，区分“物方空间”与“像方空间”的容差至关重要。下表总结了核心参数变化时，景深与焦深的响应差异。

影响因素 (Factor)	变化方向 (Change)	对景深 (DOF) 的影响 (物方空间)	对焦深 (DoFocus) 的影响 (像方空间)	物理原理 / 公式依赖
光圈系数 ($N$) (F-Number)	变大 ($F2.8 \to F11$) (光圈孔径变小)	变深 (Deep) 范围显著扩大	变深 (Deep) 焦平面容差变大	两者均与 $N$ 成正比。光束锥角变小，弥散斑扩散变慢。
镜头焦距 ($f$) (Focal Length)	变长 ($24mm \to 200mm$) (长焦镜头)	变浅 (Shallow) 背景虚化强烈	基本不变 (普通摄影距离下)	DOF $\propto 1/f^2$ (平方反比)。焦深主要取决于光圈和 $c$，与焦距无直接关系。
拍摄距离 ($u$) (Subject Distance)	变远 ($0.5m \to 50m$) (远离物体)	变深 (Deep) 且增长极快	基本不变 (除非进入微距领域)	DOF $\propto u^2$ (平方正比)。焦深主要受放大率 $m$ 影响，远距离时 $m \to 0$，焦深恒定。
允许弥散圆 ($c$) (CoC / Pixel Size)	变大 (低像素或小画幅)	变深 (Deep) 看起来更清晰	变深 (Deep) 装配精度要求降低	两者均与 $c$ 成线性正比。判定“清晰”的标准越宽松，深度越大。
放大率 ($m$) (Magnification)	变大 (微距摄影)	极浅 (Very Shallow) 毫米级景深	变深 (Deep) 显著增加	互为倒数关系 (近似)。焦深 $\approx m^2 \times$ 景深。

3. 焦深与景深的关系：纵向放大率

物理学的美妙之处在于对称性。焦深和景深实际上是共轭关系，通过纵向放大率（Longitudinal Magnification） 联系在一起。

如果你熟悉微分，我们可以对高斯公式 $\frac{1}{u} + \frac{1}{v} = \frac{1}{f}$ 进行微分：

$$
-\frac{du}{u^2} - \frac{dv}{v^2} = 0 \implies dv = - \left( \frac{v}{u} \right)^2 du
$$

其中：

$dv$ 对应焦深（像平面位置变化）。
$du$ 对应景深（物平面位置变化）。
$m = v/u$ 是横向放大率（Lateral Magnification）。

因此，我们得到一个极其优雅的近似关系：

$$
\text{焦深} \approx m^2 \times \text{景深}
$$

或者：

$$
\text{景深} \approx \frac{\text{焦深}}{m^2}
$$

深度解析

普通摄影 ($m \ll 1$)：物体很大，像很小。$m^2$ 极小。因此，景深很大，焦深很小。这意味着拍摄时我们可以容忍物体前后移动一点，但胶片/传感器必须非常精确地放置在焦平面上。
显微摄影 ($m \gg 1$)：物体很小，像很大。$m^2$ 极大。因此，景深极小，焦深很大。这意味着显微镜调节旋钮需要极其微小的移动才能对上焦，但像平面（目镜或相机）的位置反而没那么敏感。

4. 实际生活中景深和焦深影响的案例

4.1 景深案例：电影感与叙事

在电影《肖申克的救赎》中，导演经常使用浅景深将主角从背景杂乱的监狱环境中剥离出来，这种**视觉隔离（Visual Isolation）**引导观众只关注角色的表情。

技术实现：使用85mm或更大焦距的镜头，配合T1.4的大光圈。
对立面：新闻纪实摄影通常使用F8或F11的小光圈（超焦距技术），确保前景的突发事件和背景的环境信息都清晰，以交代完整的“故事上下文”。

4.2 焦深案例：光刻机 (Lithography)

这是焦深概念最昂贵的应用场景。在制造7nm或3nm芯片时，光刻机需要将纳米级的电路图案投影到硅片上。

挑战：极高的数值孔径（NA）导致焦深（DoFocus）极浅，往往只有几十纳米。
后果：如果硅片表面有微小的起伏，或者平整度不够，电路图就会模糊，导致芯片报废。
解决方案：CMP（化学机械抛光）工艺必须将晶圆表面打磨到原子级的平整，以适应极浅的焦深。

4.3 工业视觉：远心镜头 (Telecentric Lens)

在精密工业测量中，普通镜头的景深会带来透视误差（近大远小）。

应用：使用双远心镜头，不仅消除了透视误差，还通过特殊的光阑设计，在一定景深范围内保持放大倍率恒定，确保机器视觉算法测量螺丝尺寸时，不会因为传送带的轻微震动（物距变化）而得出错误数据。

5. 焦深与景深的计算 Code

为了彻底打破抽象公式的壁垒，我们编写了一套 Python 代码，不仅可以量化分析参数的影响，还能“画”出几何光学的核心原理图。

这段代码将生成两张关键图像：

参数敏感度面板：一目了然地看到光圈、焦距如何非线性地改变景深。
光路原理示意图：直观展示光线如何汇聚，以及“允许弥散圆”是如何定义焦深边界的。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches

class OpticalVisualizer:
    def __init__(self, f=50, N=2.8, c=0.029):
        self.f = f  # 焦距 (mm)
        self.N = N  # 光圈数
        self.c = c  # 弥散圆 (mm)
        self.D = f / N  # 入瞳直径 (mm)

    def plot_sensitivity_analysis(self):
        """
        绘制参数敏感度分析图：
        1. 景深 vs 拍摄距离 (不同光圈)
        2. 焦深 vs 光圈值
        3. 超焦距 vs 焦距
        """
        fig, axes = plt.subplots(1, 3, figsize=(18, 5))

        # --- 子图 1: 景深 vs 拍摄距离 ---
        u_arr = np.linspace(500, 5000, 100)  # 0.5m 到 5m
        f_stops = [1.4, 4.0, 11.0]
        colors = ['#FF5733', '#33FF57', '#3357FF']

        ax1 = axes[0]
        for i, N_val in enumerate(f_stops):
            # 近似公式计算 total DoF (为了平滑显示)
            H = (self.f ** 2) / (N_val * self.c)
            # DoF ≈ 2 u^2 N c / f^2
            dof = (2 * u_arr ** 2 * N_val * self.c) / (self.f ** 2)
            ax1.plot(u_arr / 1000, dof / 1000, color=colors[i], label=f'F/{N_val}', linewidth=2)

        ax1.set_title(f'DoF vs. Subject Distance (f={self.f}mm)')
        ax1.set_xlabel('Subject Distance [m]')
        ax1.set_ylabel('Total Depth of Field [m]')
        ax1.legend()
        ax1.grid(True, alpha=0.3)

        # --- 子图 2: 焦深 vs 光圈 ---
        N_arr = np.linspace(1.0, 22.0, 50)
        # 焦深 t = 2Nc (忽略放大率)
        dofocus = 2 * N_arr * self.c

        ax2 = axes[1]
        ax2.plot(N_arr, dofocus, color='purple', linewidth=2.5)
        ax2.fill_between(N_arr, 0, dofocus, color='purple', alpha=0.1)
        ax2.set_title(f'Depth of Focus vs. Aperture (CoC={self.c}mm)')
        ax2.set_xlabel('Aperture (F-Number)')
        ax2.set_ylabel('Depth of Focus [mm]')
        ax2.grid(True, alpha=0.3)

        # --- 子图 3: 超焦距 vs 焦距 ---
        f_arr = np.linspace(14, 200, 100)  # 14mm 到 200mm
        # H = f^2 / (Nc)
        H_arr = (f_arr ** 2) / (self.N * self.c) / 1000  # 换算为米

        ax3 = axes[2]
        ax3.plot(f_arr, H_arr, color='teal', linewidth=2.5)
        ax3.set_title(f'Hyperfocal Dist vs. Focal Length (F/{self.N})')
        ax3.set_xlabel('Focal Length [mm]')
        ax3.set_ylabel('Hyperfocal Distance [m]')
        ax3.grid(True, alpha=0.3)

        plt.tight_layout()
        plt.show()

    def draw_ray_diagram(self, u_dist_mm=1000):
        """
        绘制示意性光路图 (Schematic Ray Diagram)
        注意：为了可视化，这里的横纵坐标比例是非等比的，且大大夸张了光圈和传感器尺寸。
        """
        fig, ax = plt.subplots(figsize=(14, 6))

        # 1. 基础光学计算
        v_dist = 1 / (1 / self.f - 1 / u_dist_mm)  # 像距 v
        mag = v_dist / u_dist_mm  # 放大率

        # 焦深半宽 delta = N * c * (1+m)
        delta = self.N * self.c * (1 + mag)

        # 为了画图好看，我们需要夸张 Y 轴 (光圈) 和 X 轴 (微小的焦深)
        # 示意图坐标系：透镜中心在 (0,0)

        lens_radius = 15  # 示意性半径
        img_plane_x = 80  # 示意性像平面位置 (非真实比例)

        # 定义关键点坐标
        lens_top = (0, lens_radius)
        lens_bot = (0, -lens_radius)

        # 像点 (理想汇聚点)
        focal_point = (img_plane_x, 0)

        # --- 绘图 ---

        # A. 画透镜
        lens = patches.Ellipse((0, 0), width=5, height=lens_radius * 2.2, angle=0,
                               color='#aaddff', alpha=0.5, label='Lens')
        ax.add_patch(lens)
        ax.axvline(0, color='blue', linestyle='--', alpha=0.3)  # 透镜平面

        # B. 画光轴
        ax.axhline(0, color='black', linestyle='-', alpha=0.2)

        # C. 画光锥 (Rays) - 像方空间
        # 上边缘光线
        ax.plot([0, img_plane_x + 20], [lens_radius, -lens_radius * (20 / img_plane_x)],
                color='orange', alpha=0.8, linewidth=1)
        # 下边缘光线
        ax.plot([0, img_plane_x + 20], [-lens_radius, lens_radius * (20 / img_plane_x)],
                color='orange', alpha=0.8, linewidth=1)

        # 填充光锥
        polygon_x = [0, img_plane_x, 0]
        polygon_y = [lens_radius, 0, -lens_radius]
        ax.fill(polygon_x, polygon_y, color='orange', alpha=0.05)

        # D. 画像平面 (Sensor Plane) 和 焦深范围
        # 焦深在图中被放大显示以便观察
        dof_scale = 10  # 夸张系数
        dx = delta * dof_scale

        # 理想焦平面
        ax.axvline(img_plane_x, color='black', label='Ideal Image Plane (Sharp)', linewidth=2)

        # 焦深前界 (Near Limit)
        ax.axvline(img_plane_x - dx, color='red', linestyle='--', label='Focus Depth Limit')
        # 焦深后界 (Far Limit)
        ax.axvline(img_plane_x + dx, color='red', linestyle='--')

        # E. 画弥散圆 (CoC) 示意
        # 在焦深界限处，光线的高度应该刚好是 CoC 的一半 (示意)
        coc_h = 3  # 示意高度

        # 绘制 Near Limit 处的 CoC
        rect_near = patches.Rectangle((img_plane_x - dx - 0.5, -coc_h), 1, coc_h * 2,
                                      color='red', alpha=0.3)
        ax.add_patch(rect_near)

        # 绘制 Far Limit 处的 CoC
        rect_far = patches.Rectangle((img_plane_x + dx - 0.5, -coc_h), 1, coc_h * 2,
                                     color='red', alpha=0.3)
        ax.add_patch(rect_far)

        # 标注
        ax.annotate(r'Focus Depth ($\delta$)',
                    xy=(img_plane_x, -lens_radius / 2), xytext=(img_plane_x - 15, -lens_radius),
                    arrowprops=dict(arrowstyle='<->', color='purple'), color='purple', fontsize=12)

        ax.annotate('Circle of Confusion (CoC)',
                    xy=(img_plane_x - dx, coc_h), xytext=(img_plane_x - 30, coc_h + 5),
                    arrowprops=dict(facecolor='black', arrowstyle='->'), fontsize=10)

        # 图表设置
        ax.set_xlim(-10, 110)
        ax.set_ylim(-20, 20)
        ax.set_title(
            f'Schematic Optical Path: Depth of Focus Formation\n(Not to Scale: Axial distances compressed, CoC magnified)',
            fontsize=14)
        ax.set_xlabel('Optical Axis (Arbitrary Units)')
        ax.set_ylabel('Radial Height')
        ax.legend(loc='upper right')
        ax.set_yticks([])  # 隐藏Y轴刻度，因为是示意图

        plt.tight_layout()
        plt.show()


# --- 执行可视化 ---
if __name__ == "__main__":
    # 初始化：50mm F1.8 镜头
    viz = OpticalVisualizer(f=50, N=1.8, c=0.029)

    # 1. 绘制参数关系图
    viz.plot_sensitivity_analysis()

    # 2. 绘制光路原理图
    viz.draw_ray_diagram()

图表一：参数敏感度分析

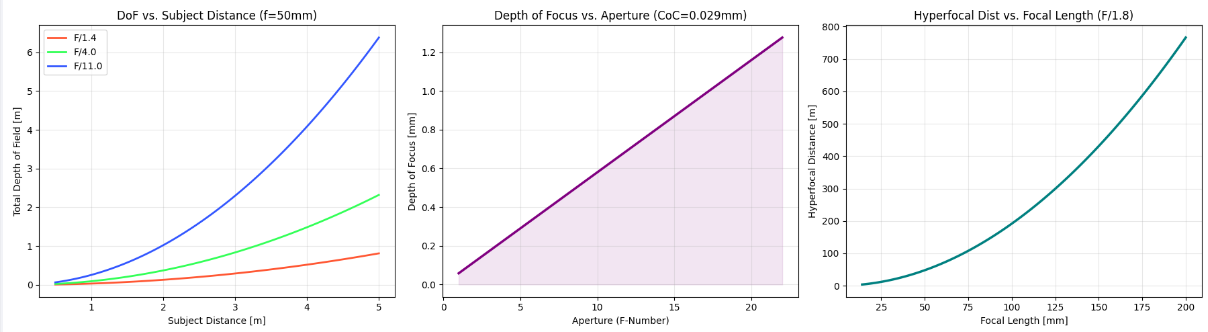
左图 (DoF vs Distance)：这是最经典的“抛物线”增长。你会发现，F11 的增长速度远快于 F1.4。这解释了为什么“退后两步”是获得大景深最廉价的方法。
中图 (DoFocus vs Aperture)：展示了极其完美的线性关系。光圈数值翻倍（光孔变小），焦深严格翻倍。这对于工业检测极其重要：如果你的零件在传送带上抖动幅度为 0.1mm，你只需要查表就能算出需要缩到多少光圈才能保证清晰。
右图 (Hyperfocal vs Focal Length)：展示了指数级的增长。焦距增加一倍，超焦距会增加四倍（$H \propto f^2$）。这就是为什么长焦镜头极难获得全景深，而广角镜头随手一拍都是清楚的。

图表二：几何光路原理 (Schematic)

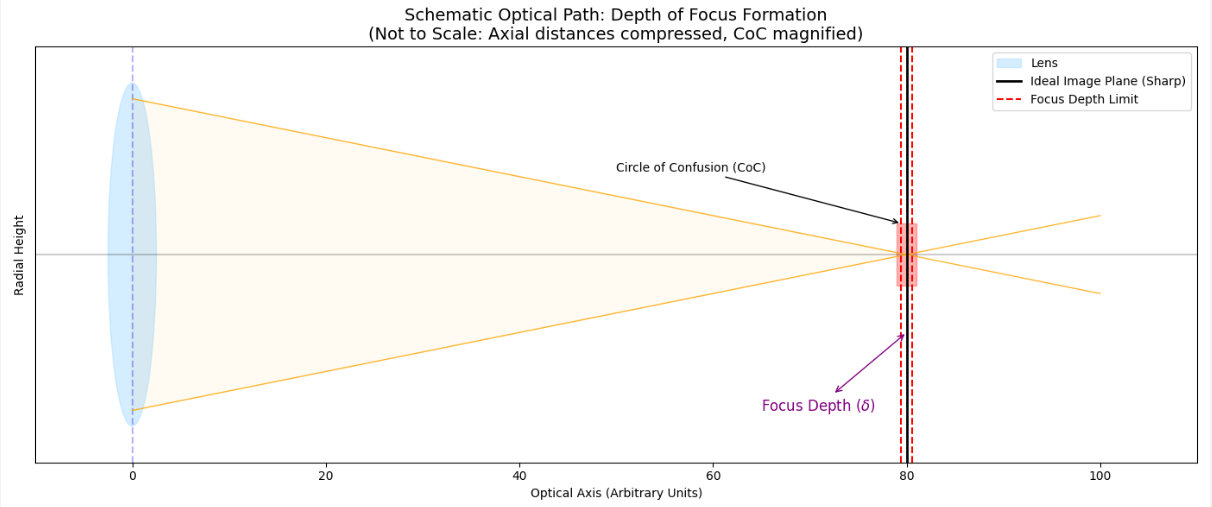
这张图是理解“模糊”本质的关键：

橙色锥体：代表光束。光圈越大，锥体底座（透镜处）越宽，锥角越大。
黑色实线 (Ideal Image Plane)：这是光线汇聚成完美一点的位置。
红色虚线 (Limits)：这是光斑扩散到允许弥散圆 (CoC) 大小的位置。
焦深 ($\delta$)：两根红色虚线之间的距离。

直观结论：如果光圈变小（透镜变窄），橙色光锥会变得更“细长”。这意味着光线在汇聚点前后的扩散速度变慢了，红色虚线就可以推得更远——这就是缩光圈增加焦深/景深的几何本质。

结语

从光的衍射到数学的近似，焦深与景深不仅仅是摄影师手中的工具，更是连接物理光学与现实世界的桥梁。理解它们，实际上是在理解光学系统传递信息的容量与限制。无论是捕捉瞬间的艺术，还是制造纳米芯片的工艺，我们都在这“清晰与模糊”的边缘上起舞。

希望通过本文的原理推导，能让你在下一次按下快门，或设计光路时，拥有更深刻的直觉。

Computational Photography

#Optics #Physics #Algorithm #Photography #Engineering

透视光影的边界：从第一性原理深度解析焦深与景深

https://sunfove.xyz/2026/01/28/2026-01-28-depth-of-field-vs-depth-of-focus-analysis/

Author

Sunfove

Posted on

January 28, 2026

Licensed under

🌍 Daily English: Beyond Conventional Optics: How Metasurfaces Are Redefining Light Manipulation | 2026-01-28 Previous

🌍 Daily English: The Architecture of Thought: How Cognitive Psychology Illuminates Mental Health | 2026-01-27 Next