虚数维度的物理投射:倏逝波、量子隧穿与光子芯片的底层逻辑
1. 引言:牛顿的困惑与几何光学的边界
早在 17 世纪,艾萨克·牛顿在研究全内反射(Total Internal Reflection, TIR)时就发现了一个奇怪的现象:如果你拿一个棱镜发生全反射,再拿另一个凸透镜紧紧压在反射面上,反射点中心会出现一个暗斑,光线竟然透过去了。
这在当时是无法解释的。按照几何光学,光线在界面处应该像台球撞击墙壁一样被完全弹回。能量要么在介质1,要么在介质2,怎么可能“跳”过真空隙?
直到麦克斯韦方程组建立后,我们才明白:物理世界的边界从来不是绝对的“墙”,场(Field)总是倾向于弥散。 全反射发生时,光场并没有在界面处突然截止,而是以一种指数衰减的形式延伸到了第二介质中,这就是倏逝波(Evanescent Wave)。
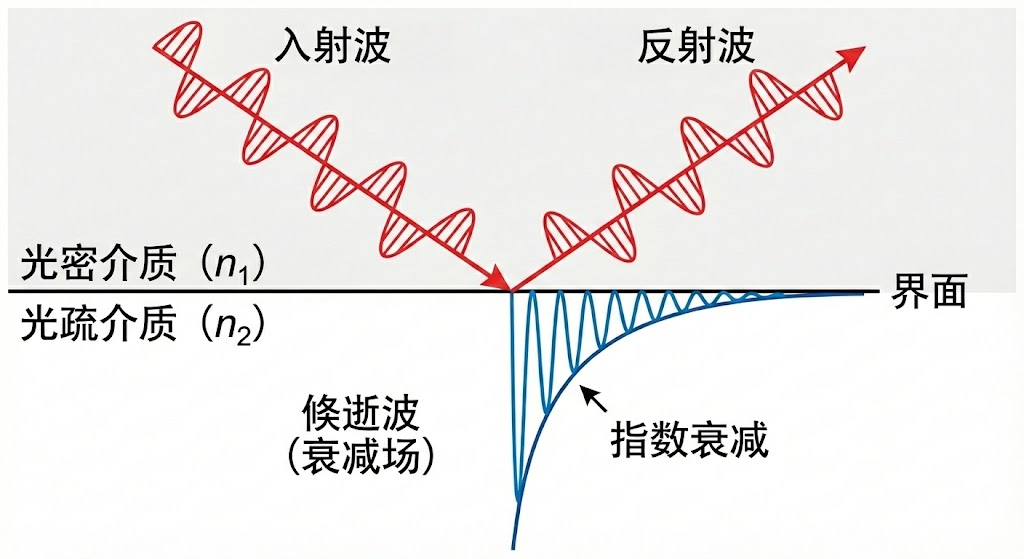
2. 第一性原理:复数波矢与波动方程的解析延拓
2.1 波动方程的通用解
设光波从高折射率介质 $n_1$ 射向低折射率介质 $n_2$($n_1 > n_2$),入射角为 $\theta_i$。在界面($z=0$)另一侧的介质2中,电场满足亥姆霍兹方程:
$$ (\nabla^2 + k_2^2) \mathbf{E} = 0 $$
其平面波解的形式为 $\mathbf{E} = \mathbf{E}_0 e^{i(\mathbf{k}_t \cdot \mathbf{r} - \omega t)}$。波矢 $\mathbf{k}_t = (k_x, 0, k_z)$ 必须满足色散关系:
$$ k_x^2 + k_z^2 = k_2^2 = \left( \frac{n_2 \omega}{c} \right)^2 $$
2.2 为什么会出现“虚数”波矢?
根据相位匹配条件(边界切向动量守恒),透射波的水平波矢 $k_x$ 必须等于入射波的水平波矢:
$$ k_x = k_{1x} = n_1 k_0 \sin \theta_i $$
当发生全反射时,$\theta_i > \theta_c = \arcsin(n_2/n_1)$,导致 $n_1 \sin \theta_i > n_2$。
此时,我们回头看 $k_z$ 的表达式:
$$ k_z^2 = k_2^2 - k_x^2 = k_0^2 (n_2^2 - n_1^2 \sin^2 \theta_i) $$
由于括号内是负数,$k_z$ 变成了纯虚数!
$$ k_z = \pm i k_0 \sqrt{n_1^2 \sin^2 \theta_i - n_2^2} \equiv \pm i \gamma $$
物理上场不能随距离发散,因此我们取 $+i\gamma$(假设 $e^{ik_z z}$ 形式)或调整符号以确保衰减。最终电场形式为:
$$ \mathbf{E}_2(x, z, t) = \mathbf{E}_0 e^{-\gamma z} e^{i(k_x x - \omega t)} $$
这里 $\gamma$ 被称为衰减系数,其倒数 $\delta = 1/\gamma$ 称为穿透深度(Penetration Depth)。对于可见光,这个深度通常在 100nm 到 500nm 之间。
2.3 TE 与 TM 模态的差异
倏逝波不仅仅只有一种。根据电场矢量的方向,分为:
- TE 模:边界条件要求切向电场连续 ($E_1 = E_2$),场强平滑过渡。
- TM 模:边界条件要求垂直方向的电位移矢量 ($D$) 连续,即 $\epsilon_1 E_{1z} = \epsilon_2 E_{2z}$。
- 由于全反射发生在光密到光疏介质 ($n_1 > n_2$),即 $\epsilon_1 > \epsilon_2$。
- 为了维持等式,透射侧的垂直电场必须被放大:$E_{2z} > E_{1z}$。
- 这种边界上的“场增强效应”使得 TM 模态携带了更高的能量密度。
虽然两者的衰减系数 $\gamma$ 相同,但它们的菲涅尔透射系数不同,这导致 TM 模的倏逝场通常比 TE 模更强。这是表面等离激元(Surface Plasmons)通常只能由 TM 光激发的数学原因。
3. 能量流动的微观机制:坡印廷矢量分析
如果场存在,能量去哪了?让我们计算第二介质中的坡印廷矢量 $\mathbf{S} = \mathbf{E} \times \mathbf{H}^*$。
3.1 垂直方向的“呼吸” (Reactive Power)
$$ \langle S_z \rangle \propto \text{Re}(E_x H_y^* - E_y H_x^) $$
由于 $k_z$ 是纯虚数,电场和磁场在 $z$ 方向上存在 $\pi/2$ 的相位差。复数的实部乘积平均值为零:
$$ \langle S_z \rangle = 0 $$
物理意义:能量并没有真正流向第二介质深处。它就像交流电路中的电容或*电感,在半个周期内能量流出界面,下半个周期能量流回界面。这是一种无功功率(Reactive Power)。
3.2 水平方向的位移:界面上的“量子滑行” (Active Power)
$$\langle S_x \rangle \neq 0$$
虽然垂直方向的能流被截止了(呈现为虚功),但在水平方向(平行于界面),情况却截然不同。能量确实沿着界面($x$ 方向)发生了真实的流动,这揭示了一个违背几何光学直觉的物理图景。
3.2.1 为什么水平能流不为零?
在 $x$ 方向上,波函数的相位因子是 $e^{i k_x x}$。
- 实数波矢:由于边界条件的限制(相位匹配),介质 2 中的水平波矢 $k_x$ 必须等于介质 1 中的水平分量 $n_1 k_0 \sin \theta_i$。这是一个纯实数。
- 相位同步:这意味着在 $x$ 方向上,电场 $\mathbf{E}$ 和磁场 $\mathbf{H}$ 的振荡步调是一致的。
- 实功传输:不同于垂直方向的 $\pi/2$ 相位差导致平均功率为零,水平方向上 $\mathbf{E}$ 和 $\mathbf{H}$ 的乘积存在非零的实部。因此,电磁能量确实在沿着界面“流淌”。
3.2.2 物理图像:贴墙滑行的光子
想象一辆赛车高速冲向弯道护栏(界面)。在几何光学中,赛车应该在接触护栏的瞬间反弹。但在波动光学中,赛车实际上切入了护栏内部(介质 2),沿着护栏边缘滑行了一段距离,然后才回到赛道(介质 1)。
场束缚与穿透深度 (Field Confinement):
这股水平流动的能量并不是像在普通透明介质中那样弥散,而是被紧紧束缚在界面附近极薄的区域内。其强度随距离 $z$ 指数衰减($e^{-\gamma z}$),主要能量集中在 穿透深度 (Penetration Depth, $\delta = 1/\gamma$) 范围内,通常仅为几百纳米。注:这与金属中的“趋肤效应”数学形式相似,但物理本质不同:倏逝波的衰减源于动量守恒的限制,而非能量被介质吸收耗散。
能量环流 (Energy Flux Loop):
如果我们绘制能流线(Poynting vector streamlines),会发现能量从介质 1 穿过界面进入介质 2,在介质 2 中平行于界面滑行一段微小距离,最终又流回介质 1。
这一现象直接导致了反射光束的重心并不是几何反射点,而是发生了一个横向位移——这正是著名的 古斯-汉兴位移(Goos-Hänchen Shift) 的物理起源。光子并没有立即反弹,它在界面上“逗留”了一会儿。
4. 古斯-汉兴位移(Goos-Hänchen Shift)
既然能量在界面上滑行了一段距离,那么反射光束的实际出射点,会相对于几何光学的预测点有一个横向位移 $D$。
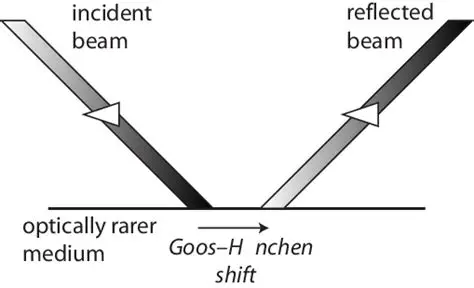
4.1 相位导数与位移
全反射系数 $r$ 是一个模为1的复数:$r = 1 \cdot e^{i \phi}$。
根据波动光学的稳相法(Stationary Phase Method),位移量 $D$ 与反射相位 $\phi$ 对入射角 $\theta$ 的导数成正比:
$$ D = - \frac{\lambda}{2\pi n_1 \cos \theta_i} \frac{d\phi}{d\theta_i} $$
4.2 物理直觉与实战演算:从公式推导到量级分析
这个位移通常只有波长量级(约 $\lambda$),在单次反射中几乎可以忽略不计。但在精密光学系统中,当光线经历成千上万次反射时,这个微小的位移会累积,产生惊人的宏观效应。
1. 理论推导:位移究竟有多大?
我们从菲涅尔反射系数的相位表达式出发。对于 TE 模(s 偏振),其反射相位 $\phi$ 满足:
$$\tan\left(\frac{\phi}{2}\right) = \frac{\sqrt{\sin^2\theta_i - n^2}}{\cos\theta_i}$$
其中 $n = n_2/n_1$ 为相对折射率。
根据 Artmann 公式,古斯-汉兴位移 $D$ 定义为相位对入射角波动的响应:
$$D = - \frac{\lambda}{2\pi n_1 \cos \theta_i} \frac{d\phi}{d\theta_i}$$
利用链式法则对相位公式求导(此处省略繁琐的三角变换步骤),我们可以得到 TE 模的精确位移解析式:
$$D_{TE} = \frac{\lambda}{\pi n_1} \frac{\sin\theta_i}{\sqrt{\sin^2\theta_i - n^2}}$$
结论:当入射角 $\theta_i$ 接近临界角($\sin\theta_i \approx n$)时,分母趋向于 0,理论位移量 $D$ 会急剧增大,远超一个波长。但在通常应用中,它保持在 $\lambda$ 量级。
2. 实战演算:20 次全反射后的累积效应
为了直观理解,我们来看一个具体的数值案例:
- 光源:假设使用红光激光,波长 $\lambda \approx 0.6 \text{ }\mu\text{m}$。
- 单次位移:假设入射角设定使得 $D \approx 1 \lambda = 0.6 \text{ }\mu\text{m}$。
- 反射次数:光束在微型谐振腔或波导中传输,经历了 20 次 全反射。
累积位移计算:
$$D_{\text{total}} = 20 \times 0.6 \text{ }\mu\text{m} = 12 \text{ }\mu\text{m}$$
3. 这个数值意味着什么?
12 微米看似微小,但在精密光学中,这是实体障碍:
谐振腔的频率漂移(Cavity Detuning):
在激光陀螺仪或法布里-珀罗腔中,谐振频率严格取决于光程长度 $L$。倏逝波导致的位移实际上增加了光在介质中的有效光程。
12 微米的额外光程远大于半波长(0.3 微米),这足以导致谐振模式发生彻底的跳变(Mode Hopping),或者在激光陀螺仪中产生巨大的零点漂移,导致导航误差。波导色散与相位延迟:
在光纤或集成波导中,虽然光不会简单地“跳出”纤芯(因为位移主要沿传播方向),但这种位移意味着光波在每次反射时都“拖慢”了脚步。这会显著改变波导的有效宽度和群速度。如果不引入量子修正,高速通信信号会产生不可控的色散,导致信号畸变。
因此,古斯-汉兴位移不再是一个理论修正量,而是光学工程师在设计高精度仪器时必须通过几何补偿来消除的关键参数。
5. 量子力学的同构:受抑全内反射 (FTIR) 与隧穿
5.1 势垒穿透模型
考虑量子力学中的方势垒问题。当粒子能量 $E$ 小于势垒高度 $V_0$ 时,薛定谔方程的解是 $e^{-\kappa x}$。这与倏逝波的数学形式完全一致。
- 介质隙 = 势垒
- 倏逝波 = 波函数在禁区的尾巴
5.2 定量计算透射率
如果在距离界面 $d$ 处放置第三种高折射率介质,倏逝波会被“捕捉”,能量流 $\langle S_z \rangle$ 不再为零。这种现象叫受抑全内反射(Frustrated Total Internal Reflection, FTIR)。
透射率 $T$ 对间隙宽度 $d$ 极其敏感:
$$ T \approx e^{-2 \gamma d} $$
这是一个指数规律。
- 应用:指纹识别仪。当手指(高折射率)按在玻璃棱镜(高折射率)上时,指纹的“脊”接触玻璃,破坏全反射(光透进手指被吸收,变暗);指纹的“谷”是空气隙,保持全反射(明亮)。这本质上是一个宏观的量子隧穿实验。
6. 现代光子学核心:耦合与传感
倏逝波不仅是理论上的数学推论,它是现代光子芯片(Silicon Photonics)和生化传感领域的命脉。在微纳尺度下,我们不再使用反射镜控制光,而是利用倏逝场的“触手”来操纵光子的流动。
6.1 定向耦合器(Directional Coupler):光子芯片的立交桥
在硅光芯片上,我们无法像焊接铜线那样简单地连接光路。为了实现光的分流与合束,工程师利用了倏逝波的横向隧穿效应。
物理机制:耦合模理论(Coupled Mode Theory)
当两根波导靠得非常近(通常间距 $< 200 \text{ nm}$)时,波导 A 中传输的光模场的倏逝尾部会覆盖到波导 B 的核心区域。这导致原本独立的两个波导模式发生了杂化(Hybridization),形成了两个新的“超模”(Supermodes):对称模和反对称模。这两个超模的相位传播常数不同,随着传播距离增加,它们产生干涉拍频。能量的钟摆效应
宏观上看,能量就像两个通过弹簧连接的钟摆。光场会周期性地从波导 A 完全流向波导 B,再流回 A。这个能量完全转移所需的距离称为耦合长度(Coupling Length, $L_c$)。工程应用
通过精确设计波导的长度 $L$:- 若 $L = L_c/2$:能量平分,制成 50:50 分束器。
- 若 $L = L_c$:光从 A 跳到了 B,制成 光交叉连接器。
- 若改变波导折射率(例如通过加热):动态改变 $L_c$,制成高速 光开关 或 调制器。
6.2 表面等离激元共振(SPR):最灵敏的生物天平
如果在全反射界面上镀一层纳米级的金膜(通常约 50nm),奇迹就会发生。特定的倏逝波能与金属表面的自由电子云(等离子体)“共舞”。
激发的苛刻条件:动量匹配
表面等离激元(SPP)是一种沿着金属表面传播的纵向电荷密度波。要激发它,入射光倏逝波的水平波矢 $k_x$ 必须严格等于 SPP 的波矢 $k_{spp}$。
$$k_{photon} \sin\theta = k_{spp}$$
这通常只能由 TM 偏振光(磁场平行于界面,电场有垂直分量)在特定的共振角下触发。Kretschmann 结构与全吸收
当角度匹配时,光子的能量被瞬间“吸干”,转化为金属表面的电子振荡。在反射光谱上,我们会看到一个尖锐的吸收深谷。传感原理:指数级敏感
SPP 的场也是一种倏逝场,且被极度压缩在金属表面 $200 \text{ nm}$ 范围内。这意味着它对表面附近的折射率变化极其敏感。- 应用场景:这是生物制药领域的金标准。当抗原与抗体在金膜表面结合时,仅仅几纳米的蛋白质层厚度增加,就会显著改变表面折射率,导致 SPR 共振角发生偏移。科学家无需对样品进行标记(Label-free),就能实时监测分子的结合过程。
7. 结语:不可见的桥梁
倏逝波向我们展示了物理实在的微妙之处,在那个看似黑暗的指数衰减区域,光子并没有消失,它在以一种虚拟的态势,探索着周围环境的每一个原子。正是这种“探出墙外的头”,让我们得以实现光子芯片的互联、单分子的探测以及对量子隧穿本质的理解。从某种意义上说,现代通信网络的每一个比特,都曾在光纤的包层中经历过倏逝波的洗礼。