算法之美：模拟退火算法的物理原理与数学表述

在组合优化领域，模拟退火算法（Simulated Annealing, SA）常被视为一种通用的随机搜索启发式算法。然而，它的核心并非简单的随机游走，而是统计力学在计算科学中的完美投影。

本文将解析该算法如何通过模拟热力学系统演化，将物理世界的“能量最低态”映射为数学世界的“全局最优解”。

第一章：物理本源 —— 统计力学与自由能的博弈

在物理世界中，大自然解决“复杂系统优化问题”的方式非常独特：它不微观地指挥每一个原子去哪里，而是制定一个宏观的概率规则，让亿万原子在热运动中自己找到最舒适的位置（能量最低态）。

这个宏观规则，就是玻尔兹曼分布。

1.1 上帝的骰子：什么是玻尔兹曼分布？

在热力学中，当我们研究一个与恒温热库（温度 $T$）保持接触的封闭系统（物理上称为正则系综）时，系统处于某一特定微观状态 $i$ 的概率 $P_i$ 并非均等，而是严格由该状态的能量 $E_i$ 决定的。

这就是著名的玻尔兹曼分布 (Boltzmann Distribution)：

$$
P_i(T) = \frac{1}{Z(T)} \exp\left(-\frac{E_i}{k_B T}\right)
$$

这个公式看似抽象，实则包含三个核心物理直觉：

  1. 指数衰减 ($e^{-E}$)：
    能量越低，概率越大；能量越高，概率呈指数级下降。

    • 为什么是指数形式？ 因为对于两个独立的子系统，总能量是相加的 ($E_{total} = E_1 + E_2$)，而联合概率是相乘的 ($P_{total} = P_1 \times P_2$)。只有指数函数能满足这种将“加法”转化为“乘法”的数学特性 ($e^{a+b} = e^a \cdot e^b$)，即在能量和概率之间建立联系。

  2. 温度项 ($T$)：
    温度作为分母出现在指数中，它是系统对“高能量”状态的容忍度。

    • 高温时：$T$ 很大，指数项趋近于 0 ($e^0=1$)，能量高低造成的概率差异被抹平，系统处于“混乱”状态。
    • 低温时：$T$ 很小，指数项差异被急剧放大，低能态的概率远高于高能态，系统被“锁定”在有序状态。

  3. 配分函数 ($Z$)：
    $$Z(T) = \sum_{j} \exp(-E_j / k_B T)$$
    这是所有可能状态概率的归一化因子（Normalization Constant），确保所有概率之和为 1。

    • 注：在实际算法中，$Z$ 的计算涉及遍历所有解空间，是不可行的。这也是为什么我们需要后文的 Metropolis 准则——通过计算两个状态的概率比率来消去 $Z$。

1.2 深度原理：自由能最小化 ($F = E - TS$)

为什么自然界会遵循这种分布？为什么高温下系统喜欢混乱，低温下喜欢有序？

这源于热力学第二定律。在恒温条件下，系统演化的终极目标并非单纯的“能量 $E$ 最小化”，而是**“赫尔姆霍兹自由能 (Helmholtz Free Energy)”** $F$ 的最小化。

自由能的定义揭示了模拟退火的根本动力：

$$
F = E - T \cdot S
$$

  • $E$ (Internal Energy)：系统的内能。对应优化问题中的目标函数值。
  • $S$ (Entropy)：系统的熵。对应解空间的多样性或无序度。
  • $T$ (Temperature)：温度。对应算法的控制参数。

这个公式解释了算法行为的本质博弈：

  1. 当温度极高时 ($T \to \infty$)：
    公式中 $-TS$ 项（熵项）占据绝对主导。为了最小化 $F$，系统倾向于最大化熵 $S$。

    • 物理现象：金属熔化为液态，原子剧烈运动，排列极度无序。
    • 算法映射：算法忽略能量 $E$ 的高低，以近乎均匀的概率遍历整个解空间。这对应全局搜索 (Exploration)。

  2. 当温度极低时 ($T \to 0$)：
    $-TS$ 项趋近于 0，能量 $E$ 项占据主导。为了最小化 $F$，系统必须最小化能量 $E$。

    • 物理现象：原子被锁定在晶格节点上，形成规则且稳定的晶体。
    • 算法映射：算法变得“贪婪”，只接受能量更低的状态，拒绝任何能量升高的尝试。这对应局部收敛 (Exploitation)。

1.3 直观理解：概率地形的重塑

让我们通过计算概率比率，看看温度 $T$ 是如何重塑解空间的概率地形的。

假设有两个状态：优解 A ($E_A=10$) 和 差解 B ($E_B=30$)。它们的相对概率比率为：

$$
\frac{P(B)}{P(A)} = \frac{e^{-30/T}}{e^{-10/T}} = \exp\left(-\frac{20}{T}\right)
$$

  • 高温 ($T=1000$)：比率 $\approx e^{-0.02} \approx 0.98$。
    此时，差解 B 出现的概率几乎和优解 A 一样！系统“看不清”好坏，能够轻易翻越能量壁垒，从 A 跳到 B。
  • 低温 ($T=1$)：比率 $= e^{-20} \approx 2 \times 10^{-9}$。
    此时，差解 B 出现的概率微乎其微。系统被牢牢“锁”在优解 A 附近。

!

总结： 模拟退火算法的本质，就是模拟自然界从“熵驱动（高温、无序、全局）”平滑过渡到“能量驱动（低温、有序、局部）”的过程。我们在计算机中重演了这一物理奇迹，从而在庞大的解空间中“生长”出最优解。

二、 算法核心：Metropolis 准则

在计算机中直接计算配分函数 $Z(T)$ 通常是不可行的（涉及对所有可能状态求和，属于 #P-complete 问题）。

1953年，Metropolis 等人提出了一种巧妙的采样方法，无需计算 $Z(T)$ 即可从玻尔兹曼分布中采样。其核心在于计算两个状态之间的概率比。

2.1 状态转移推导

假设系统当前处于状态 $i$（能量 $E_i$），试图转移到状态 $j$（能量 $E_j$）。根据玻尔兹曼分布，两者的概率比为：

$$
\frac{P_j}{P_i} = \frac{\frac{1}{Z} e^{-E_j / kT}}{\frac{1}{Z} e^{-E_i / kT}} = \exp\left( - \frac{E_j - E_i}{kT} \right)
$$

定义能量差 $\Delta E = E_j - E_i$。

2.2 接受概率公式

Metropolis 准则定义了从 $i$ 接受转移到 $j$ 的概率 $A_{ij}$：

$$
A_{ij} = \min\left(1, \exp\left(-\frac{\Delta E}{T}\right)\right)
$$

这个分段函数包含了两个物理逻辑：

  1. **若 $\Delta E < 0$**（新状态能量更低）：指数项 $> 1$，取最小值 1。意味着必定接受更优解。
  2. 若 $\Delta E \ge 0$（新状态能量更高）：以概率 $e^{-\Delta E / T}$ 接受。意味着以一定概率容忍劣解。

正是这一概率性接受劣解的机制（Metropolis Criterion），使得算法具有了**跳出局部极小值（Local Minima）**的能力。

三、 随机过程视角：马尔可夫链

从随机过程的角度看，模拟退火算法在每一个固定的温度 $T_k$ 下，都在构造一个时齐马尔可夫链（Homogeneous Markov Chain）。

3.1 细致平衡条件 (Detailed Balance)

为了保证该马尔可夫链的平稳分布（Stationary Distribution）确实是玻尔兹曼分布，转移概率矩阵 $P$ 必须满足细致平衡条件：

$$
\pi_i P_{ij} = \pi_j P_{ji}
$$

其中 $\pi_i$ 是玻尔兹曼分布概率。Metropolis 准则的构造正是为了满足这一等式。这意味着，在温度 $T$ 保持不变且迭代次数足够多的情况下，算法生成的解序列将在概率上收敛于玻尔兹曼分布。

3.2 冷却进度 (Cooling Schedule)

由于我们最终需要的是 $T \to 0$ 时的分布，算法变成了一个非时齐马尔可夫链。Geman 和 Geman (1984) 证明了，要保证算法以概率 1 收敛到全局最优，温度 $T_k$ 的下降速度需满足：

$$
T_k \ge \frac{c}{\ln(1+k)}
$$

这被称为对数冷却。但在工程实践中，因其收敛过慢，我们通常采用指数冷却（Geometric Cooling）作为近似：

$$
T_{k+1} = \alpha \cdot T_k \quad (\alpha \in [0.8, 0.99])
$$

四、 算法实现与可视化

为了直观感受模拟退火的“物理过程”，我们编写一个带有实时可视化功能的 Python 脚本。

我们将优化一个经典的非凸函数：$f(x) = x^2 + 10\sin(x)$。这个函数在全局最低点附近布满了局部陷阱，非常适合用来演示 SA 算法如何“跳出”局部最优。

4.1 Python 可视化代码

请确保你的环境中安装了 matplotlib (pip install matplotlib)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
import numpy as np
import matplotlib.pyplot as plt


# --- 1. 定义目标函数 ---
def objective_function(x):
    return x ** 2 + 10 * np.sin(x)


# --- 2. 模拟退火算法 
def run_sa_clean_result():
    # === A. 参数设置 ===
    bounds = [-10, 10]
    T = 100.0
    T_min = 0.01
    alpha = 0.98
    iter_per_temp = 50

    # === B. 初始化 ===
    # 随机生成起点
    start_x = np.random.uniform(bounds[0], bounds[1])
    start_e = objective_function(start_x)

    # 当前状态 & 最优状态
    current_x = start_x
    current_e = start_e
    best_x = current_x
    best_e = current_e

    print(f"初始位置: x={start_x:.4f}, E={start_e:.4f}")
    print("正在计算中...")

    # === C. 纯计算循环 (无需记录轨迹，只记结果) ===
    while T > T_min:
        for _ in range(iter_per_temp):
            perturbation = np.random.normal(0, 1) * (T * 0.1)
            new_x = current_x + perturbation
            new_x = np.clip(new_x, bounds[0], bounds[1])
            new_e = objective_function(new_x)

            # Metropolis
            delta_e = new_e - current_e
            if delta_e < 0:
                accept = True
            else:
                prob = np.exp(-delta_e / T)
                accept = np.random.random() < prob

            if accept:
                current_x = new_x
                current_e = new_e
                if current_e < best_e:
                    best_x = current_x
                    best_e = current_e

        T *= alpha

    print(f"计算结束！最优解: x={best_x:.4f}, E={best_e:.4f}")
    print("正在生成结果图...")

    # === D. 极简绘图 ===
    fig, ax = plt.subplots(figsize=(12, 6))

    # 1. 绘制背景函数曲线 (清晰的深灰色)
    x_grid = np.linspace(bounds[0], bounds[1], 1000)
    y_grid = objective_function(x_grid)
    ax.plot(x_grid, y_grid, color='#444444', linewidth=2, label='Objective Function')

    # 2. 绘制起点 (蓝色方块)
    ax.scatter(start_x, start_e, color='blue', marker='s', s=100, label='Start Point', zorder=5)

    # 3. 绘制终点/最优解 (绿色大五角星)
    ax.scatter(best_x, best_e, color='#00FF00', marker='*', s=350, edgecolors='black',
               label=f'Global Best\n(E={best_e:.4f})', zorder=10)

    # 4. 添加漂亮的标注箭头 (Annotate)
    # 给起点加箭头
    ax.annotate('Start Here', xy=(start_x, start_e), xytext=(start_x, start_e + 20),
                arrowprops=dict(facecolor='blue', shrink=0.05),
                fontsize=10, ha='center')

    # 给终点加箭头
    ax.annotate('Found Minimum', xy=(best_x, best_e), xytext=(best_x, best_e + 30),
                arrowprops=dict(facecolor='green', shrink=0.05),
                fontsize=12, fontweight='bold', ha='center')

    # 5. 美化布局
    ax.set_title(f"Simulated Annealing Result\nFinal Best: x={best_x:.4f}, E={best_e:.4f}", fontsize=14)
    ax.set_xlabel("x value")
    ax.set_ylabel("Energy")
    ax.grid(True, linestyle='--', alpha=0.5)
    ax.legend()

    plt.tight_layout()
    plt.show()


if __name__ == "__main__":
    run_sa_clean_result()

最终运行结果如图所示

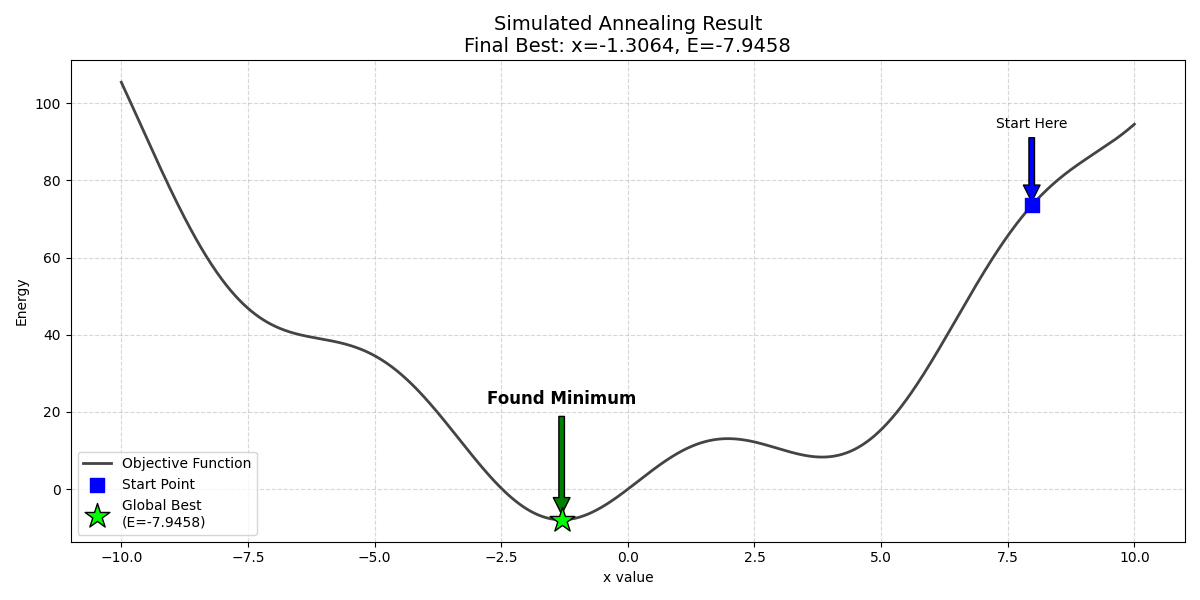
五、 总结与展望

模拟退火算法的魅力在于其简洁背后的深刻物理意义。

  1. 全局观：它利用高温阶段的**熵增（Entropy maximization）**机制，赋予了算法“遍历”解空间的能力。
  2. 局部观：它利用低温阶段的**能量最小化（Energy minimization）**机制，保证了最终解的精度。
  3. 平衡：温度 $T$ 实际上是“探索（Exploration）”与“利用（Exploitation）”之间的平衡因子。

尽管在深度学习等梯度敏感领域，SA 已不再是主流，但在离散组合优化（如 TSP、车间调度、芯片布局）以及无梯度黑盒优化场景中，基于坚实物理原理的模拟退火算法依然是不可或缺的利器。

Computer Science > Theoretical Computer Science
#Python #Algorithm #Optimization #Mathematics #Statistical Mechanics
算法之美：模拟退火算法的物理原理与数学表述
https://sunfove.xyz/2026/01/23/2026-01-23-simulated-annealing-physics-optimization/
Author
Sunfove
Posted on
January 23, 2026
Licensed under