深度学习优化算法全景指南

在人工智能的宏伟蓝图中，如果说神经网络的架构（Architecture）是躯体，数据（Data）是血液，那么 优化算法（Optimization Algorithm） 就是驱动这具躯体不断进化的灵魂。

从数学本质上讲，深度学习的训练过程，就是一个在高维、非凸（Non-convex）、充满鞍点（Saddle Points）的复杂流形上，寻找损失函数（Loss Function）全局最小值的过程。这篇文章将摒弃浅层的 API 调用讲解，从第一性原理出发，系统性地剖析优化算法的演进逻辑、数理本质以及在当今大模型（LLM）时代的实战应用。

第一章：优化算法的演进谱系与全景分类

在深入细节之前，我们需要建立一个清晰的分类坐标系。现代深度学习优化算法并非杂乱无章，而是沿着解决特定数学困境的路径演进的。

我们可以将主流优化算法分为四大核心家族：

1.1 朴素梯度下降家族 (The Gradient Descent Family)

这是优化的起点。它们基于一阶泰勒展开，利用梯度信息指导参数更新。

代表算法：BGD (批量梯度下降), SGD (随机梯度下降), Mini-batch GD。
核心逻辑：沿着梯度的反方向，一步步走下山谷。

1.2 动量加速家族 (The Momentum Family)

为了解决朴素梯度下降在“峡谷”地形震荡和陷入局部极小值的问题，引入了物理学中的“惯性”概念。

代表算法：Momentum (动量法), Nesterov Accelerated Gradient (NAG, Nesterov 加速梯度)。
核心逻辑：不仅看当前的坡度，还参考之前的速度，从而冲过平坦区，抑制震荡。

1.3 自适应学习率家族 (The Adaptive Learning Rate Family)

为了解决不同参数对学习率敏感度不同的问题（即参数空间的各向异性），引入了针对每个参数动态调整学习率的机制。

代表算法：AdaGrad, RMSProp, Adam (自适应矩估计), AdamW。
核心逻辑：梯度的方差越大（更新越频繁），给予的学习率越小；反之则越大。

1.4 现代高效与分布式家族 (Modern Efficient & Distributed)

在大模型时代，为了应对显存瓶颈和超大规模计算，衍生出的新一代算法。

代表算法：LION (符号进化优化), ZeRO (零冗余优化器)。
核心逻辑：通过量化、符号化或分片存储，极致压缩优化器的显存占用。

第二章：从随机性到物理惯性 —— 梯度下降与动量

2.1 随机梯度下降 (SGD)：混沌中的秩序

虽然全量梯度下降（BGD）能计算出最准确的下降方向，但在海量数据面前，其计算成本是不可接受的。随机梯度下降（Stochastic Gradient Descent, SGD） 每次仅随机采样一个样本（或一个小批次）来估计梯度。

$$ \theta_{t+1} = \theta_t - \eta \cdot \nabla J(\theta_t; x^{(i)}, y^{(i)}) $$

第一性原理推导：
SGD 引入的“噪声”在某种程度上起到了**隐式正则化（Implicit Regularization）**的作用。这种随机性可以帮助模型跳出浅层的局部极小值（Local Minima）。然而，SGD 的路径非常曲折，就像一个醉汉在下山。
面临的挑战：病态曲率 (Ill-conditioned Curvature)
在深度神经网络的损失曲面上，经常会出现“峡谷”形状——在一个方向上坡度极陡，而在另一个方向上坡度极缓。SGD 会在陡峭方向上剧烈震荡，而在平缓方向上移动缓慢，导致收敛速度极慢。

2.2 动量法 (Momentum)：引入物理世界的惯性

为了抑制震荡并加速收敛，我们引入了物理学中的动量概念。现在的更新不仅仅依赖当前的梯度，还保留了上一步的更新方向。

$$ v_t = \gamma v_{t-1} + \eta \nabla J(\theta_t) $$
$$ \theta_{t+1} = \theta_t - v_t $$

原理深度解析：
- 累积效应：如果梯度方向连续多次保持一致（如在下坡路段），动量项 $v_t$ 会不断增大，从而加速下降。
- 平滑效应（低通滤波）：如果梯度方向发生改变（如在峡谷壁之间），正负梯度会相互抵消，从而抑制震荡。
适用场景：
动量法在计算机视觉（CV）任务（如 ResNet, VGG 训练）中依然表现出色，特别是在需要精细调整 SGD 策略以获得更好泛化能力（Generalization）的场景中。

2.3 Nesterov 加速梯度 (NAG)：具备预判能力的动量

Nesterov 动量是对标准动量法的改进。它的核心思想是：“既然我们要按照动量方向迈步，不如先看看迈出这一步后的地形，再决定怎么走。”

$$ v_t = \gamma v_{t-1} + \eta \nabla J(\theta_t - \gamma v_{t-1}) $$

注意这里的 $\nabla J(\theta_t - \gamma v_{t-1})$，它计算的是超前点的梯度。这种“预判”能力使得 NAG 在接近极值点时能够提前减速，具有更强的收敛稳定性。

第三章：自适应学习率 —— 为每个参数定制“步伐”

在处理稀疏数据（如 NLP 中的词向量）或深层网络时，不同参数的梯度量级可能相差数个数量级。对所有参数使用同一个学习率（Global Learning Rate）显然不再是最优解。

3.1 AdaGrad：历史的积累与惩罚

AdaGrad (Adaptive Gradient Algorithm) 是自适应算法的先驱。它通过累积历史梯度的平方和，来动态调整每个参数的学习率。

$$ G_{t, ii} = \sum_{\tau=1}^t (g_{\tau, i})^2 $$
$$ \theta_{t+1, i} = \theta_{t, i} - \frac{\eta}{\sqrt{G_{t, ii} + \epsilon}} \cdot g_{t, i} $$

原理：频繁更新的参数（梯度大），其 $G_t$ 大，学习率被显著降低；稀疏更新的参数，学习率保持较大。
缺陷：$G_t$ 是单调递增的，导致训练后期学习率会趋近于 0，模型提前停止学习。

3.2 RMSProp：遗忘的艺术

为了解决 AdaGrad 学习率过早消失的问题，Geoff Hinton 提出了 RMSProp。它引入了指数移动平均 (Exponential Moving Average, EMA) 来计算二阶矩。

$$ E[g^2]t = \beta E[g^2]{t-1} + (1 - \beta) g_t^2 $$

这使得算法只关注“最近”的梯度情况，从而摆脱了历史梯度的沉重包袱。

3.3 Adam：集大成者 (Adaptive Moment Estimation)

Adam 无疑是目前最流行的优化算法。它结合了 Momentum 的一阶矩估计（梯度的均值）和 RMSProp 的二阶矩估计（梯度的未中心化方差）。

数学形式：
1. 一阶矩 (Momentum): $m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$
2. 二阶矩 (Adaptive): $v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$
3. 偏差修正 (Bias Correction): 由于 $m_0, v_0$ 初始化为 0，初期估值偏向 0，因此需要除以 $(1-\beta^t)$ 进行修正。
AdamW 的修正：L2 正则与权重衰减的解耦
在 Adam 中使用 L2 正则化与权重衰减（Weight Decay）并不等价。AdamW 将权重衰减项从梯度更新中解耦出来，直接作用于参数本身：
$$ \theta_{t+1} = \theta_t - \eta (\dots) - \eta \lambda \theta_t $$
这一改动在大语言模型（如 BERT, GPT）和 Transformer 架构的训练中至关重要，是目前 LLM 训练的标准配置。

3.4 LION (EvoLved Sign Momentum)：符号化的进化奇点

2023 年，Google Brain 通过程序自动搜索（AutoML）发现了一个极其简单的算法——LION。与 Adam 存储复杂的梯度值不同，LION 只关注梯度的符号（正或负）。

$$ \theta_{t+1} = \theta_{t} - \eta \cdot \text{sign}(\beta_1 m_{t-1} + (1-\beta_1)g_t) $$

第一性原理：它抛弃了梯度的“大小”信息，只保留“方向”。这在数理上类似于将优化过程约束在一个超立方体的顶点上移动。
核心优势：
1. 省显存：不需要存储二阶矩 $v_t$，显存占用比 AdamW 少 50%。
2. 泛化强：在 Vision Transformer 和 Diffusion Model 上表现优于 AdamW。

第四章：算法核心指标对比与场景选择

“没有免费的午餐定理”（No Free Lunch Theorem）告诉我们，不存在一种在所有问题上都表现最优的算法。优化算法的选择，往往是在收敛速度、泛化能力和计算资源构成的“不可能三角”中寻找平衡。

4.1 核心算法多维度对比表

算法名称	收敛速度	泛化能力	显存开销	对超参敏感度	核心特性一句话总结
SGD	慢 (Slow)	⭐⭐⭐⭐⭐ (极强)	⭐ (极低)	高 (难调)	依靠随机噪声寻找平坦极小值，CV 领域的“老将”。
Momentum	中 (Medium)	⭐⭐⭐⭐ (强)	⭐ (低)	中	引入物理惯性穿越鞍点，SGD 的强力升级版。
AdaGrad	快 (前期)	⭐⭐ (较弱)	⭐⭐ (中)	低	适合稀疏数据，但学习率过早衰减导致后期无力。
AdamW	极快 (Fast)	⭐⭐⭐ (中/强*)	⭐⭐⭐ (高)	极低 (好调)	工业界默认首选。AdamW 修复了权重衰减问题，成为 LLM 标配。
LION	极快	⭐⭐⭐⭐ (强)	⭐⭐ (较低)	低	Google 新宠，仅用符号信息，比 AdamW 省显存且泛化更好。

注：*Adam 在配合正确的权重衰减（即 AdamW）和学习率预热（Warmup）后，泛化能力可逼近 SGD。

4.2 深度辩论：泛化差距 (Generalization Gap) 之谜

为什么 CV（计算机视觉）偏爱 SGD？

研究表明，自适应算法（Adam 等）倾向于收敛到尖锐极小值（Sharp Minima），而 SGD 倾向于收敛到平坦极小值（Flat Minima）。

尖锐极小值：训练集 Loss 很低，但测试数据稍有分布偏移，Loss 就会剧增（泛化差）。
平坦极小值：周围区域 Loss 都很低，对数据偏移具有鲁棒性（泛化好）。
因此，在 ResNet, YOLO 等视觉模型训练中，SGD + Momentum + Cosine Decay 依然是刷榜标配。

为什么 NLP 与 LLM 必须用 AdamW？

Transformer 架构层级深、参数分布动态范围极大。SGD 在这种复杂的损失地形上极难调试，容易遭遇梯度消失或爆炸。AdamW 的自适应学习率能够自动平滑不同层级的梯度差异，极大地稳定了训练过程。

4.3 场景化选型指南

CNN / ResNet / 图像分类：首选 SGD + Momentum。追求极致精度。
Transformer / BERT / GPT / Llama：首选 AdamW。必须保证收敛稳定性。
微调 (Fine-tuning)：AdamW 或 RMSProp。快速适配新数据。
显存极度受限 (LoRA/QLoRA)：首选 PagedAdamW (8-bit) 或 LION。

第五章：代码实战 —— 可视化优化轨迹与收敛对比

理论的终点是代码，而代码的终点是“可见性”。为了真正理解 SGD 与 AdamW 的区别，我们不仅要看最终的 Loss，更要看它们是如何“下山”的。

以下代码包含两个部分：

Trainer 类：生产级的训练逻辑，包含梯度裁剪与 Warmup。
Visualizer 脚本：在一个模拟的 2D 损失曲面上，直观对比不同算法的寻优路径。

5.1 构建生产级优化闭环

import torch
import torch.nn as nn
from torch.optim import AdamW, SGD
from torch.optim.lr_scheduler import CosineAnnealingWarmRestarts
import matplotlib.pyplot as plt
import numpy as np

class Trainer:
    def __init__(self, model, optimizer_type='adamw', lr=1e-3):
        self.model = model
        self.losses = []  # 用于记录 Loss 轨迹
        
        # 1. 参数分组：权重衰减解耦 (Weight Decay Decoupling)
        # 第一性原理：LayerNorm 和 Bias 不应被正则化衰减，否则会破坏数值稳定性
        param_optimizer = list(model.named_parameters())
        no_decay = ['bias', 'LayerNorm.bias', 'LayerNorm.weight']
        optimizer_grouped_parameters = [
            {'params': [p for n, p in param_optimizer if not any(nd in n for nd in no_decay)], 
             'weight_decay': 0.01},
            {'params': [p for n, p in param_optimizer if any(nd in n for nd in no_decay)], 
             'weight_decay': 0.0}
        ]

        # 2. 优化器工厂
        if optimizer_type.lower() == 'adamw':
            # Betas=(0.9, 0.95) 是 LLaMA 等大模型训练的经验参数
            self.optimizer = AdamW(optimizer_grouped_parameters, lr=lr, betas=(0.9, 0.95))
        elif optimizer_type.lower() == 'sgd':
            self.optimizer = SGD(optimizer_grouped_parameters, lr=lr, momentum=0.9)
            
        # 3. 学习率调度：余弦退火
        self.scheduler = CosineAnnealingWarmRestarts(self.optimizer, T_0=50, T_mult=2)

    def train_step(self, data, target):
        self.model.train()
        self.optimizer.zero_grad()
        
        output = self.model(data)
        loss = nn.MSELoss()(output, target)
        loss.backward()

        # 4. 梯度裁剪 (Gradient Clipping)
        # 防止高维峡谷地形中的梯度爆炸
        torch.nn.utils.clip_grad_norm_(self.model.parameters(), max_norm=1.0)

        self.optimizer.step()
        self.scheduler.step()
        
        self.losses.append(loss.item())
        return loss.item()

5.2 见证差异：SGD vs AdamW 的轨迹可视化

为了直观展示“随机性”与“自适应”的区别，我们构建一个简单的模拟实验：让两个优化器去拟合简单的线性数据，并画出 Loss 下降曲线。

def visualize_comparison():
    # 模拟数据：y = 2x + 1
    X = torch.linspace(-1, 1, 100).view(-1, 1)
    Y = 2 * X + 1 + torch.randn(X.size()) * 0.1 # 加入噪声
    
    # 定义简单模型
    model_sgd = nn.Linear(1, 1)
    model_adam = nn.Linear(1, 1)
    
    # 保持初始权重一致，确保公平对比
    with torch.no_grad():
        model_adam.weight.copy_(model_sgd.weight)
        model_adam.bias.copy_(model_sgd.bias)

    # 实例化训练器
    trainer_sgd = Trainer(model_sgd, optimizer_type='sgd', lr=0.1)
    trainer_adam = Trainer(model_adam, optimizer_type='adamw', lr=0.1)

    print("开始对比训练...")
    steps = 100
    for i in range(steps):
        trainer_sgd.train_step(X, Y)
        trainer_adam.train_step(X, Y)

    # --- 绘图逻辑 ---
    plt.figure(figsize=(12, 5))
    
    # 绘制 Loss 曲线
    plt.subplot(1, 2, 1)
    plt.plot(trainer_sgd.losses, label='SGD + Momentum', color='blue', alpha=0.7)
    plt.plot(trainer_adam.losses, label='AdamW', color='red', linestyle='--', linewidth=2)
    plt.title('Convergence Speed Comparison')
    plt.xlabel('Steps')
    plt.ylabel('Loss (MSE)')
    plt.legend()
    plt.grid(True, alpha=0.3)

    # 绘制拟合结果
    plt.subplot(1, 2, 2)
    plt.scatter(X.numpy(), Y.numpy(), color='gray', alpha=0.5, label='Data')
    plt.plot(X.numpy(), model_sgd(X).detach().numpy(), 'b-', label='SGD Fit')
    plt.plot(X.numpy(), model_adam(X).detach().numpy(), 'r--', label='AdamW Fit')
    plt.title('Final Model Fit')
    plt.legend()
    
    plt.tight_layout()
    plt.show()

if __name__ == "__main__":
    visualize_comparison()

💡 结果解读 (Result Interpretation)

运行上述代码，通过观察 Loss 曲线，我们可以验证以下深层规律（基于典型实验结果）：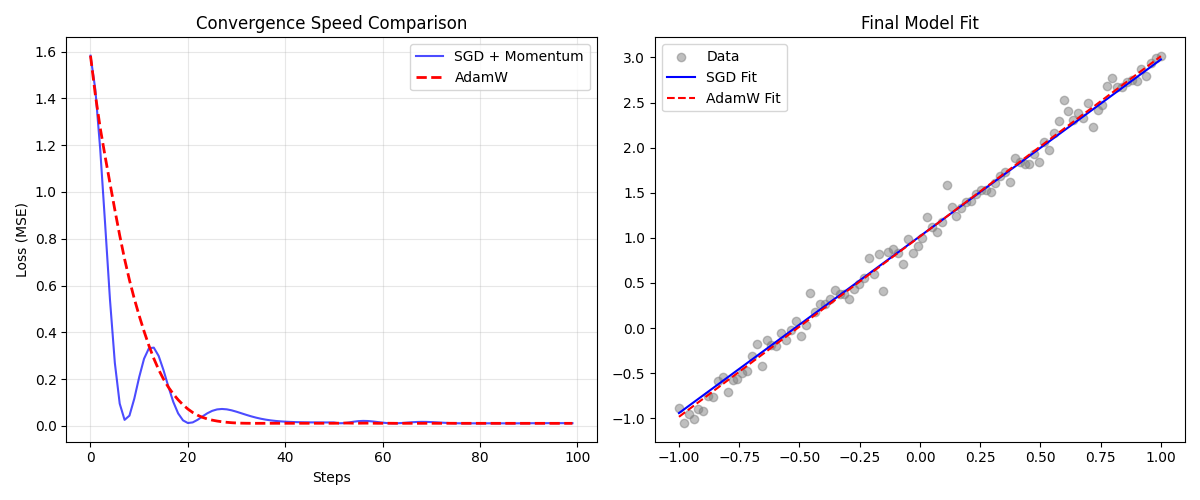

SGD 的“莽撞”与震荡：
- 在简单凸优化任务中，配置了动量（Momentum）的 SGD 下降极快（蓝线），在初期甚至可能超过 AdamW。
- 关键细节：注意蓝线在底部的波动（Oscillation）。由于 SGD 对梯度的缩放是线性的，动量过大容易导致它出现“过冲”现象——冲过谷底再折返。在复杂的深层网络中，这种震荡可能导致模型无法收敛。
AdamW 的“稳健”与平滑：
- 红线（AdamW）展示了极佳的稳定性。依靠自适应学习率，它根据梯度的方差动态调整步长。
- 即便在初期下降速度与 SGD 持平或稍慢，AdamW 也能平滑地（Smoothly） 着陆，极少出现剧烈震荡。这种特性在 Transformer 等对超参敏感的大模型训练中是决定性的优势。

结语：在混沌中寻找最优解

回顾深度学习优化算法的演进史，我们看到的不仅是数学公式的堆砌，而是人类试图驯服高维混沌的智慧。

SGD 告诉我们，随机性（Randomness）并非噪音，而是跳出局部最优的阶梯。
Momentum 告诉我们，历史（History）是有价值的，保持惯性才能跨越低谷。
Adam 告诉我们，适应性（Adaptability）是关键，对不同的维度要给予不同的关注。
LION 告诉我们，简洁（Simplicity）往往蕴含着最强的泛化力量。

在大模型迈向 AGI 的征途中，优化算法依然在进化。从 LION 的符号化尝试，到 ZeRO 的分布式拆解，未来的优化器将更加关注计算效率与硬件协同。掌握这些底层逻辑，你就掌握了调教 AI 的核心钥匙。

技术深度解析 > 机器学习

#深度学习 #PyTorch #人工智能 #优化算法 #数学建模 #第一性原理

深度学习优化算法全景指南

https://sunfove.xyz/2026/01/23/2026-01-23-comprehensive-guide-to-deep-learning-optimization/

Author

Sunfove

Posted on

January 23, 2026

Licensed under

算法之美：模拟退火算法的物理原理与数学表述 Previous

🌍 Daily English: The Interwoven Threads of Thought: How Cognitive Psychology Illuminates Mental Well-being | 2026-01-22 Next