深度解析海森矩阵：从二阶曲率到高维优化

在多变量微积分和现代优化理论的宏大建筑中，梯度（Gradient）指引了我们前进的方向，而**海森矩阵（Hessian Matrix）**则揭示了地形的起伏与坎坷。对于任何致力于理解深度学习、物理模拟或经济学建模的研究者而言，理解海森矩阵不仅是掌握数学工具的需求，更是培养高维空间直觉的关键。

本文将摒弃死记硬背的定义，从泰勒级数（Taylor Series）的第一性原理出发，推导海森矩阵的由来，通过特征值分解解析其几何意义，并最终探讨其在**牛顿法（Newton’s Method）**及现代机器学习中的应用。

1. 第一性原理：从泰勒展开说起

要理解海森矩阵，我们必须回到微积分的基石——泰勒级数。泰勒级数告诉我们，任何光滑函数都可以在某一点附近被多项式近似。

1.1 单变量函数的近似

对于一个单变量函数 $f(x)$，在点 $x_0$ 附近的二阶泰勒展开为：

$$
f(x) \approx f(x_0) + f’(x_0)(x - x_0) + \frac{1}{2}f’’(x_0)(x - x_0)^2
$$

这里有三个关键项：

  1. 常数项 $f(x_0)$：当前的函数值。
  2. 一阶项 $f’(x_0)$：斜率，告诉我们要增加函数值应该往哪个方向走。
  3. 二阶项 $f’’(x_0)$：曲率（Curvature），告诉我们斜率变化得有多快（是凸的还是凹的）。

1.2 推广到多变量：海森矩阵的诞生

当我们进入多维空间，输入变成向量 $\mathbf{x} \in \mathbb{R}^n$，函数 $f: \mathbb{R}^n \rightarrow \mathbb{R}$ 输出一个标量。此时，泰勒展开的形式变为：

$$
f(\mathbf{x}) \approx f(\mathbf{x}_0) + \nabla f(\mathbf{x}_0)^T (\mathbf{x} - \mathbf{x}_0) + \frac{1}{2} (\mathbf{x} - \mathbf{x}_0)^T \mathbf{H}(\mathbf{x}_0) (\mathbf{x} - \mathbf{x}_0)
$$

在这个公式中：

  • $\nabla f(\mathbf{x}_0)$ 是梯度向量，对应一阶导数。
  • $\mathbf{H}(\mathbf{x}_0)$ 正是海森矩阵，对应二阶导数。

定义：海森矩阵是一个 $n \times n$ 的方阵，由函数 $f$ 对各个分量的二阶偏导数组成：

$$
\mathbf{H}(f) = \begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \
\vdots & \vdots & \ddots & \vdots \
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}
\end{bmatrix}
$$

或者更紧凑地写为 $\mathbf{H}_{ij} = \frac{\partial^2 f}{\partial x_i \partial x_j}$。

关键性质：如果函数 $f$ 的二阶偏导数是连续的，根据施瓦茨定理（Schwarz’s Theorem），混合偏导数相等，即 $\frac{\partial^2 f}{\partial x_i \partial x_j} = \frac{\partial^2 f}{\partial x_j \partial x_i}$。这意味着海森矩阵是对称矩阵（Symmetric Matrix）。这一性质至关重要，因为它保证了海森矩阵的特征值全部为实数，且特征向量相互正交。

2. 几何意义：曲率与地形分析

海森矩阵本质上描述了高维函数的局部几何结构。在梯度为零的临界点（Critical Point），一阶项消失，函数的局部行为完全由二阶项（即海森矩阵）主导。

这一项 $\frac{1}{2} \Delta \mathbf{x}^T \mathbf{H} \Delta \mathbf{x}$ 是一个二次型（Quadratic Form）。为了理解形状，我们需要对 $\mathbf{H}$ 进行特征值分解。

2.1 特征值与凸性

设 $\mathbf{H}$ 的特征值为 $\lambda_1, \lambda_2, \dots, \lambda_n$，对应的单位特征向量为 $\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n$。我们可以通过坐标变换将二次型对角化。

局部地形的形状完全取决于特征值 $\lambda_i$ 的符号：

  1. 正定（Positive Definite）：

    • 所有特征值 $\lambda_i > 0$。
    • 几何形状：碗状（Bowl）。函数在所有方向上都向上弯曲。
    • 结论：该点是局部极小值。

  2. 负定（Negative Definite）：

    • 所有特征值 $\lambda_i < 0$。
    • 几何形状：倒扣的碗。函数在所有方向上都向下弯曲。
    • 结论：该点是局部极大值。

  3. 不定（Indefinite）：

    • 存在 $\lambda_i > 0$ 和 $\lambda_j < 0$。
    • 几何形状：马鞍面（Saddle）。在某些方向（对应正特征值）是极小值，在另一些方向（对应负特征值）是极大值。
    • 结论：该点是鞍点（Saddle Point）。

Hessian Geometry Placeholder
(图注：鞍点的几何示意图，展示了不同方向上的曲率差异)

2.2 条件数与病态曲率

特征值的大小不仅决定了方向，还决定了弯曲的程度。

  • 如果 $\lambda_{\max} \gg \lambda_{\min} > 0$，说明函数在一个方向上非常陡峭（山谷壁），而在另一个方向上非常平坦（山谷底）。
  • 海森矩阵的条件数（Condition Number） $\kappa = \frac{|\lambda_{\max}|}{|\lambda_{\min}|}$ 衡量了这种各向异性。

这种情况被称为病态曲率（Ill-conditioned curvature），它是梯度下降法（Gradient Descent）的大敌。在病态条件下，梯度下降会在峡谷壁之间来回震荡，收敛极慢。

3. 优化中的深度应用：牛顿法 (Newton’s Method)

在优化领域，梯度下降（Gradient Descent）通常被比作“盲人下山”——通过脚下的坡度（一阶导数）来决定下一步的方向。而牛顿法则像是“睁开了眼睛”，它利用海森矩阵提供的曲率信息（二阶导数），看清了地形的局部全貌，从而做出更明智的跳跃。

3.1 第一性原理：从线性逼近到二次逼近

优化的核心思想是用一个简单的函数去局部逼近复杂的非线性函数 $f(\mathbf{x})$，然后求这个简单函数的极小值。

  • 梯度下降利用的是一阶泰勒展开（线性逼近）：它将局部地形看作一个平面。
    $$ f(\mathbf{x}) \approx f(\mathbf{x}_0) + \nabla f(\mathbf{x}_0)^T (\mathbf{x} - \mathbf{x}_0) $$
    平面没有极小值（它会无限延伸下去），所以我们需要人为设定一个步长（Learning Rate）走一步停下来看看。

  • 牛顿法利用的是二阶泰勒展开（二次逼近）：它将局部地形看作一个二次曲面（碗状抛物面）。
    $$ f(\mathbf{x}) \approx f(\mathbf{x}_0) + \nabla f(\mathbf{x}_0)^T (\mathbf{x} - \mathbf{x}_0) + \frac{1}{2} (\mathbf{x} - \mathbf{x}_0)^T \mathbf{H}(\mathbf{x}_0) (\mathbf{x} - \mathbf{x}_0) $$
    二次曲面是有明确的底部的（极小值点）。牛顿法的策略非常直接：直接跳到这个近似抛物面的底部。

3.2 推导与几何直觉

我们要找到步长向量 $\Delta \mathbf{x} = \mathbf{x} - \mathbf{x}_0$，使得上述二次近似函数取得极小值。
对 $\Delta \mathbf{x}$ 求导并令其为 0：

$$
\nabla_{\Delta \mathbf{x}} \left( \nabla f^T \Delta \mathbf{x} + \frac{1}{2} \Delta \mathbf{x}^T \mathbf{H} \Delta \mathbf{x} \right) = 0 \
\nabla f + \mathbf{H} \Delta \mathbf{x} = 0
$$

解出 $\Delta \mathbf{x}$：

$$ \Delta \mathbf{x} = - \mathbf{H}^{-1} \nabla f $$

这就是著名的牛顿更新公式：
$$ \mathbf{x}_{n+1} = \mathbf{x}_n - \mathbf{H}^{-1}(\mathbf{x}_n) \nabla f(\mathbf{x}_n) $$

3.3 为什么 $\mathbf{H}^{-1}$ 是完美的自适应学习率？

在梯度下降中，更新公式是 $\mathbf{x}_{n+1} = \mathbf{x}_n - \alpha \nabla f$。对比牛顿法，你会发现矩阵 $\mathbf{H}^{-1}$ 取代了标量学习率 $\alpha$。这是一个质的飞跃：

  1. 各向异性校正（Anisotropic Correction）：
    普通的梯度下降在所有维度上使用相同的标量 $\alpha$。但在高维空间中，地形往往是“狭长”的（比如在一个方向平坦，另一个方向陡峭）。

    • 在陡峭的方向（曲率大，$\mathbf{H}$ 的特征值大），我们需要小心移动。$\mathbf{H}^{-1}$ 会自动缩小该方向的步长。
    • 在平坦的方向（曲率小，$\mathbf{H}$ 的特征值小），我们需要大步流星。$\mathbf{H}^{-1}$ 会自动放大该方向的步长。

  2. 仿射不变性（Affine Invariance）：
    牛顿法的性能不受坐标系缩放的影响。如果你把某个特征的单位从“米”改成“毫米”，梯度下降的收敛路径会剧烈改变（变得更难收敛），需要重新调参。而牛顿法通过 $\mathbf{H}^{-1}$ 的左乘，在数学上抵消了这种线性变换。

3.4 收敛速度：二次收敛的威力

牛顿法拥有二次收敛（Quadratic Convergence）速度。这意味着在接近极值点时，每迭代一步，解的有效数字位数就会翻倍。

如果误差序列是 $e_n = |x_n - x^*|$，那么：

  • 梯度下降：$e_{n+1} \approx c \cdot e_n$ （线性收敛）
  • 牛顿法：$e_{n+1} \approx c \cdot e_n^2$ （二次收敛）

比如误差从 $0.01$ ($10^{-2}$) 变到 $0.0001$ ($10^{-4}$)，下一步就是 $10^{-8}$。这种速度在精确科学计算中是毁灭性的优势。

3.5 致命缺陷：为何在 AI 中受阻？

虽然理论完美，但在深度学习中直接应用牛顿法面临三大“拦路虎”：

  1. 维度的诅咒：计算 $n \times n$ 的 Hessian 矩阵并求逆，复杂度是 $O(n^3)$。对于一亿参数的模型 ($n=10^8$)，这在现有物理宇宙中是不可计算的。
  2. 鞍点的陷阱：牛顿法寻找的是梯度为0的点。如果海森矩阵是不定的（Indefinite），牛顿法可能会被吸引到鞍点甚至极大值点（因为它总是试图走向曲率为0的地方，而不分凸凹）。
  3. 非凸性：全局来看，神经网络的 Loss Surface 极其复杂，二阶近似只在极小范围（Trust Region）内有效，盲目应用牛顿大步长会导致算法飞出这一区域，造成发散。

因此，现代优化器（如 Adam, RMSProp）实际上是在通过仅使用一阶梯度信息来模拟海森矩阵对角线元素的缩放效果，这被称为“拟牛顿法”的一种轻量级变体。

理解了海森矩阵描述了曲率后，我们就可以利用这一信息来加速优化。普通的梯度下降法只利用了一阶信息（线性近似），它盲目地沿着最陡峭的方向走，而不考虑前方地形的变化。

牛顿法（Newton’s Method） 利用了二阶信息（二次近似）。

3.6 代码实战：牛顿法 vs 梯度下降

为了直观感受海森矩阵的威力，我们构建一个二维的“峡谷”函数：
$$ f(x, y) = x^2 + 10y^2 $$

这是一个典型的病态条件函数：

  • $x$ 方向平坦（系数 1）。
  • $y$ 方向陡峭（系数 10）。
  • 等高线呈现狭长的椭圆形。

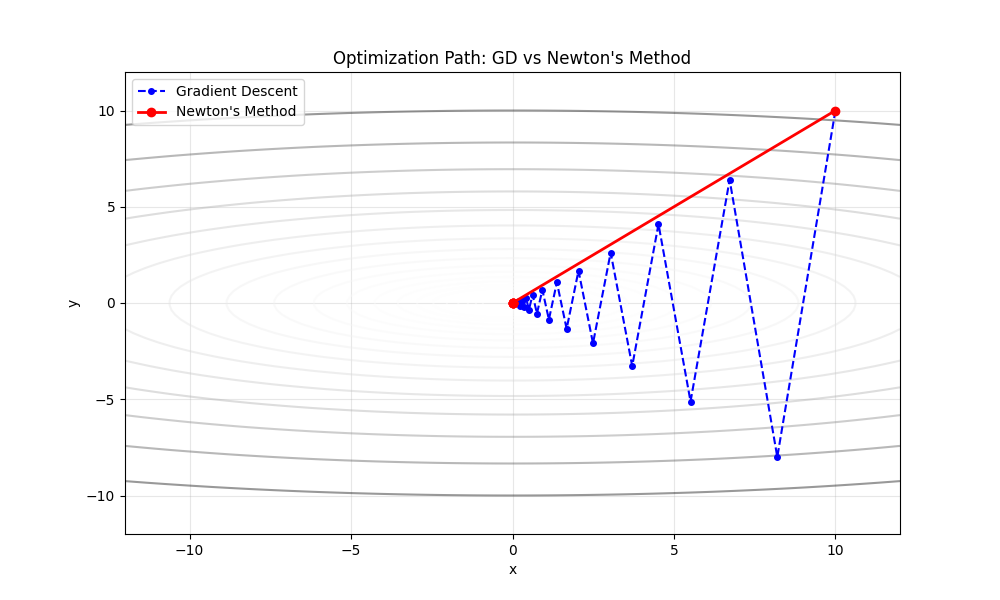
在这个函数上，普通的梯度下降（GD）如果不精心调整学习率，很容易在峡谷壁之间来回震荡（Zig-zag），收敛缓慢。而牛顿法利用海森矩阵的信息，理论上应该能瞬间找到谷底。

我们用 Python 来模拟这一过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import numpy as np
import matplotlib.pyplot as plt

# 1. 定义目标函数及其导数
def func(x):
    # f(x, y) = x^2 + 10y^2
    return x[0]**2 + 10 * x[1]**2

def gradient(x):
    # 梯度向量 [2x, 20y]
    return np.array([2*x[0], 20*x[1]])

def hessian(x):
    # 海森矩阵 [[2, 0], [0, 20]]
    # 注意：对于二次函数，海森矩阵是常数矩阵
    return np.array([[2, 0], 
                     [0, 20]])

# 2. 优化算法实现
def run_gradient_descent(start_point, lr=0.09, steps=20):
    path = [start_point]
    x = start_point.copy()
    for _ in range(steps):
        grad = gradient(x)
        x = x - lr * grad
        path.append(x)
    return np.array(path)

def run_newtons_method(start_point, steps=5):
    path = [start_point]
    x = start_point.copy()
    for _ in range(steps):
        grad = gradient(x)
        H = hessian(x)
        # 牛顿法核心更新公式：x = x - H^-1 * g
        # np.linalg.solve(A, b) 求解 Ax = b，比求逆更高效稳定
        step = np.linalg.solve(H, grad) 
        x = x - step
        path.append(x)
    return np.array(path)

# 3. 运行对比
start_point = np.array([10.0, 10.0]) # 从 (10, 10) 开始

# 梯度下降 (学习率设为 0.09)
gd_path = run_gradient_descent(start_point)

# 牛顿法
newton_path = run_newtons_method(start_point)

# 4. 可视化绘图
x = np.linspace(-12, 12, 100)
y = np.linspace(-12, 12, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2

plt.figure(figsize=(10, 6))
plt.contour(X, Y, Z, levels=np.logspace(0, 3, 20), cmap='gray_r', alpha=0.4)

# 绘制梯度下降路径 (蓝色虚线)
plt.plot(gd_path[:, 0], gd_path[:, 1], 'b--o', label='Gradient Descent', markersize=4)

# 绘制牛顿法路径 (红色实线)
plt.plot(newton_path[:, 0], newton_path[:, 1], 'r-o', label="Newton's Method", linewidth=2)

plt.title("Optimization Path: GD vs Newton's Method")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

# 输出最后几步的结果
print(f"GD Final Position: {gd_path[-1]}")
print(f"Newton Final Position: {newton_path[-1]}")

结果分析

运行上述代码，你会看到一幅极具冲击力的画面：

  1. 梯度下降（蓝色路径）：
    由于 $y$ 方向梯度太大，算法被迫在峡谷两壁之间剧烈震荡（Zig-zagging）。它花费了许多步才慢慢接近原点。如果你稍微增大一点学习率，它甚至会发散。

  2. 牛顿法（红色路径）：
    只有一步。是的，仅仅一步。
    从起点 $(10, 10)$ 直接跳到了全局最优解 $(0, 0)$。

为什么？
因为我们优化的目标是一个二次函数。牛顿法的二阶泰勒近似对二次函数是精确的（没有高阶误差项）。海森矩阵的逆 $H^{-1}$ 完美地消除了各个方向的曲率差异，将椭圆形的等高线在数学变换空间中变成了正圆形，使得算法可以直接沿着直线走到中心。

这就是二阶优化的魅力所在：它利用曲率信息，将“弯路”变“直路”。

4. 计算机视觉中的深度应用：Hessian Blob Detector

在图像处理中，我们不再处理抽象的 $n$ 维向量，而是处理离散的像素网格。此时，图像 $I(x, y)$ 被视为一个强度曲面（Intensity Surface）。

海森矩阵在这里扮演了二阶特征检测器的角色。不同于梯度（一阶导数）检测“边缘”（强度突变），海森矩阵（二阶导数）检测的是“斑点”（Blob）——即各个方向都存在强度变化的区域。

4.1 直觉：特征值与地形分类

回顾前文，海森矩阵 $\mathbf{H}$ 的特征值 $\lambda_1, \lambda_2$ 决定了曲面的局部形状。在图像中，这意味着什么？

我们关注海森矩阵的行列式（Determinant）：
$$
\text{Det}(\mathbf{H}) = \lambda_1 \cdot \lambda_2 = I_{xx} I_{yy} - (I_{xy})^2
$$

我们可以根据特征值的符号将图像区域分类：

  1. 平坦区域 ($\lambda_1 \approx 0, \lambda_2 \approx 0$)：

    • $\text{Det}(\mathbf{H}) \approx 0$。
    • 这是背景区域，无特征。

  2. 边缘区域 ($\lambda_1 \gg 0, \lambda_2 \approx 0$ 或反之)：

    • 一个方向曲率大，另一个方向平坦（像排水沟）。
    • $\text{Det}(\mathbf{H}) \approx 0$。
    • 关键点：海森矩阵的行列式会抑制边缘响应！这是它优于拉普拉斯算子（Laplacian, $\lambda_1 + \lambda_2$）的地方，后者容易对边缘产生误报。

  3. 斑点区域 ($\lambda_1, \lambda_2$ 绝对值都很大且同号)：

    • 亮斑（山峰）：$\lambda_1 < 0, \lambda_2 < 0$。
    • 暗斑（盆地）：$\lambda_1 > 0, \lambda_2 > 0$。
    • 在这两种情况下，$\text{Det}(\mathbf{H}) = \lambda_1 \lambda_2 > 0$（且数值很大）。

结论：寻找图像中 $\text{Det}(\mathbf{H})$ 的局部极大值点，就是寻找完美的斑点中心。

4.2 尺度空间理论（Scale Space）

现实中的斑点有大有小。如果直接在原始像素上求导，我们只能检测到极其微小的噪点。为了检测不同大小的斑点，必须引入高斯尺度空间。

我们用不同标准差 $\sigma$ 的高斯核 $G(x, y, \sigma)$ 与图像进行卷积：

$$
L(x, y, \sigma) = G(x, y, \sigma) * I(x, y)
$$

此时，海森矩阵的元素变为对平滑后图像 $L$ 的导数。根据卷积的性质，导数运算可以转移到高斯核上：

$$
I_{xx}(\sigma) = I(x, y) * \frac{\partial^2 G}{\partial x^2}(\sigma)
$$

为了使不同尺度的响应具有可比性，我们需要进行尺度归一化，乘以 $\sigma^2$。最终的**尺度归一化海森行列式（Hessian Determinant）**响应函数为：

$$
\text{Response}(x, y, \sigma) = \sigma^2 (L_{xx}L_{yy} - L_{xy}^2)
$$

4.3 从理论到工程：SURF 算法

计算高斯卷积非常耗时。SURF (Speeded Up Robust Features) 算法通过工程近似解决了这个问题：

  1. 方框滤波（Box Filters）：它使用简单的矩形区域（Box Filter）近似二阶高斯导数模板 $\frac{\partial^2 G}{\partial x^2}$。
  2. 积分图（Integral Image）：利用积分图技术，任意大小的方框滤波均可在 $O(1)$ 时间内计算完成。

这使得 SURF 能够实时计算海森矩阵的行列式，从而实现极快的特征点检测。

4.4 代码实战：从零实现海森斑点检测

为了展示第一性原理，我们不使用现成的库，而是使用 Python 主要是 Numpy 和 Scipy 手动计算海森行列式图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter
import cv2

def compute_hessian_determinant(image, sigma):
    """
    计算给定尺度 sigma 下的 Hessian 矩阵行列式响应图
    """
    # 1. 归一化因子，用于尺度不变性
    # 理论上是 sigma^2，但在离散导数中通常需要根据滤波器大小调整
    scale_norm = sigma ** 2

    # 2. 计算高斯平滑后的二阶导数
    # 直接对高斯平滑后的图像求中心差分近似
    
    # 先进行高斯模糊
    smooth_img = gaussian_filter(image, sigma=sigma)
    
    # 使用 Sobel 算子或简单的梯度函数计算二阶导数
    # gradients 返回 (dy, dx)
    dy, dx = np.gradient(smooth_img)
    dyy, dyx = np.gradient(dy)
    dxy, dxx = np.gradient(dx)
    
    # 3. 构建海森矩阵元素
    I_xx = dxx
    I_yy = dyy
    I_xy = dxy  # 或者是 dyx，两者理论上相等
    
    # 4. 计算行列式 det(H) = Ixx * Iyy - Ixy^2
    # 乘以 scale_norm 进行归一化
    det_H = scale_norm * (I_xx * I_yy - I_xy**2)
    
    return det_H, smooth_img

# --- 主程序 ---

# 生成一个合成图像：包含不同大小的亮点
img_size = 200
image = np.zeros((img_size, img_size))

# 添加斑点 (y, x, radius)
blobs = [
    (50, 50, 2),   # 小斑点
    (100, 120, 5), # 中斑点
    (150, 50, 10)  # 大斑点
]

for (y, x, r) in blobs:
    # 简单的圆形高斯斑点模拟
    yy, xx = np.ogrid[:img_size, :img_size]
    mask = ((yy - y)**2 + (xx - x)**2) <= r**2 * 2
    image[mask] = 1.0

# 添加一些噪声
np.random.seed(42)
image += np.random.normal(0, 0.05, image.shape)

# 选择一个特定的尺度进行检测 (尝试匹配中等斑点)
target_sigma = 5.0
response_map, smooth_img = compute_hessian_determinant(image, target_sigma)

# 可视化
plt.figure(figsize=(12, 4))

plt.subplot(1, 3, 1)
plt.title("Original Image")
plt.imshow(image, cmap='gray')
plt.axis('off')

plt.subplot(1, 3, 2)
plt.title(f"Smoothed (sigma={target_sigma})")
plt.imshow(smooth_img, cmap='gray')
plt.axis('off')

plt.subplot(1, 3, 3)
plt.title(f"Hessian Determinant\n(Blob Response)")
plt.imshow(response_map, cmap='jet') # jet 颜色图能清晰显示高响应区
plt.colorbar()
plt.axis('off')

plt.tight_layout()
plt.show()

运行上述代码，我们可能会得到类似下图的结果（假设 target_sigma=5.0）：

Hessian Blob Detection Result
(图注：左图为原始噪声图像；中图为高斯平滑结果；右图为海森行列式响应)

观察右侧的响应图，我们可以验证尺度空间理论的三个关键推论：

  1. 完美匹配（强响应）：
    中间的斑点（$r=5$）在 $\sigma=5.0$ 的检测下响应最强（红色中心）。这说明当检测尺度与特征尺寸一致时，海森行列式取得极大值。这就是 SURF 算法确定特征点大小的原理。

  2. “甜甜圈”效应（尺度过小）：
    左下角的大斑点（$r=10$）呈现出空心的环状结构。这是因为 $\sigma=5.0$ 的算子太小，只能感知到大斑点边缘的曲率变化，而无法覆盖整个斑点中心。要检测它，我们需要增大 $\sigma$。

  3. 过度平滑（尺度过大）：
    左上角的小斑点（$r=2$）几乎消失。因为 $\sigma=5.0$ 的高斯核已经将它完全模糊掉，融入了背景。

结论：没有万能的 $\sigma$。真正的特征提取算法（如 SIFT/SURF）会构建一个高斯金字塔，在连续的尺度空间中寻找 $(x, y, \sigma)$ 的局部极值点，从而实现对不同大小物体的鲁棒检测。

5. 总结

海森矩阵连接了线性代数与微积分，是理解高维函数几何特性的金钥匙。

  • 从定义上看：它是二阶偏导数的集合。
  • 从几何上看：它的特征值决定了函数的凸凹性和鞍点结构，条件数决定了优化的难度。
  • 从应用上看：它是牛顿法等二阶优化算法的核心，虽然在高维深度学习中直接应用受限，但其思想通过拟牛顿法和自适应学习率算法（如Adam）得以延续。

掌握海森矩阵，意味着你不再仅仅是在梯度下降的黑暗中摸索，而是拥有了感知地形起伏的雷达。

Technical Deep Dive > Artificial Intelligence
#Optimization #Linear Algebra #Machine Learning #Mathematics #Calculus
深度解析海森矩阵：从二阶曲率到高维优化
https://sunfove.xyz/2026/01/22/2026-01-22-hessian-matrix-geometry-and-optimization/
Author
Sunfove
Posted on
January 22, 2026
Licensed under