超越分组：聚类算法的第一性原理深度解析

引言：混沌中的秩序与认知的本质

人类认知的基石在于“分类”。早在古希腊时期，柏拉图在《费德鲁斯篇》中就借苏格拉底之口提出了“按照自然关节将事物切分（Carving nature at its joints）”的思想。这便是聚类（Clustering）的哲学雏形：在没有先验标签（Label）指导的情况下，如何从混沌的数据中发现内在的结构与秩序？

在机器学习领域，聚类作为无监督学习（Unsupervised Learning）的核心支柱，其本质并非简单的“分组”，而是对数据流形（Data Manifold）拓扑结构的探索，是对**熵（Entropy）**的最小化尝试。

本文将摒弃对 API 的肤浅调用，转而从数学的第一性原理出发，解构聚类算法背后的几何学、概率论与线性代数基础，并通过实战代码验证不同算法视角的差异。

---

第一章：相似性的几何本质 (The Geometry of Similarity)

聚类的核心问题可以归结为一个定义问题：什么是“相似”？

在数学上，相似性通常通过距离度量（Distance Metric）的倒数来体现。一个度量空间 $(M, d)$ 必须满足非负性、对称性和三角不等式。

1.1 欧几里得空间的局限与诅咒

最直观的度量是欧几里得距离（Euclidean Distance）：

$$
d(x, y) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}
$$

然而，从第一性原理来看，欧式距离假设了空间的各向同性（Isotropy），即所有特征维度的权重和尺度是等同的。但在高维空间中，我们面临“维度诅咒（Curse of Dimensionality）”。

随着维度 $d \to \infty$，任意两点之间的距离趋向于相等。这意味着在高维空间中，基于欧式距离的聚类将失效，因为“最近邻”和“最远邻”的差异变得微不足道。

1.2 马哈拉诺比斯距离 (Mahalanobis Distance)

为了修正特征间的相关性和尺度差异，我们引入协方差矩阵 $\Sigma$。马哈拉诺比斯距离考虑了数据的分布形状：

$$
d_M(x, y) = \sqrt{(x - y)^T \Sigma^{-1} (x - y)}
$$

如果 $\Sigma$ 是单位矩阵，则退化为欧式距离。这一视角的引入，让我们意识到聚类不仅仅是点与点的几何关系，更是点与分布统计特性之间的关系。

---

第二章：K-Means 的变分法视角 (A Variational Perspective on K-Means)

K-Means 是最普及的算法，但很少有人从优化理论的角度去审视它。

2.1 目标函数的推导

K-Means 的本质是一个非凸优化问题。我们的目标是最小化簇内方差（Intra-cluster Variance），也就是最小化惯性（Inertia）。

设数据集为 $X = {x_1, …, x_n}$，我们要将其划分为 $k$ 个集合 $S = {S_1, …, S_k}$，以最小化以下目标函数 $J$：

$$
J = \sum_{i=1}^{k} \sum_{x \in S_i} ||x - \mu_i||^2
$$

其中 $\mu_i$ 是 $S_i$ 的质心。

2.2 期望最大化 (EM) 算法的特例

K-Means 实际上是 EM 算法（Expectation-Maximization）在硬聚类（Hard Clustering）下的一个特例。

• E-Step (Assignment): 固定质心 $\mu_i$，将每个点 $x$ 分配给最近的 $\mu_i$。这相当于构建了 Voronoi 泰森多边形。
• M-Step (Update): 固定分配方案，更新质心 $\mu_i$ 为该簇内所有点的均值。

$$
\frac{\partial J}{\partial \mu_i} = -2 \sum_{x \in S_i} (x - \mu_i) = 0 \implies \mu_i = \frac{1}{|S_i|} \sum_{x \in S_i} x
$$

2.3 局限性的几何解释

由于 K-Means 依赖于 Voronoi 划分，它隐含地假设簇是**凸形（Convex）**且各向同性的。对于环形、新月形或长条形的数据分布，K-Means 会强行将其切割为凸多边形，从而导致错误的聚类。

---

第三章：概率生成的视角——高斯混合模型 (GMM)

如果我们承认现实世界充满了不确定性，那么硬聚类（要么属于A，要么属于B）就是一种过于武断的简化。

3.1 软聚类与隐变量

高斯混合模型（Gaussian Mixture Model, GMM）假设数据是由 $K$ 个高斯分布线性叠加而成的。这里的“聚类”不再是划分，而是参数估计。

数据的概率密度函数为：

$$
P(x) = \sum_{k=1}^{K} \pi_k \mathcal{N}(x | \mu_k, \Sigma_k)
$$

其中：

• $\pi_k$ 是混合系数（Mixing Coefficient），满足 $\sum \pi_k = 1$。
• $\mathcal{N}(x | \mu_k, \Sigma_k)$ 是第 $k$ 个高斯分量。
• $\Sigma_k$ 是协方差矩阵，它允许簇呈现椭圆形，从而突破了 K-Means 的各向同性限制。

3.2 似然函数最大化

我们需要最大化对数似然函数（Log-Likelihood）：

$$
\ln p(X | \pi, \mu, \Sigma) = \sum_{n=1}^{N} \ln \left{ \sum_{k=1}^{K} \pi_k \mathcal{N}(x_n | \mu_k, \Sigma_k) \right}
$$

从物理学的角度看，GMM 试图找到数据分布的“势能面”，通过高斯势阱来捕捉数据点。

---

第四章：密度的拓扑——DBSCAN 与 谱聚类

当数据结构极其复杂，甚至嵌入在非欧流形上时（例如瑞士卷 Swiss Roll 数据），传统的距离度量失效。我们需要将数据转化为图（Graph），利用谱图理论（Spectral Graph Theory）进行切分。

4.1 谱聚类：从几何到图论

我们将每个数据点视为图 $G=(V, E)$ 的顶点。边权重 $W_{ij}$ 表示点 $i$ 和点 $j$ 的相似度。定义度矩阵 $D$ 为对角矩阵，拉普拉斯矩阵定义为 $L = D - W$。

谱聚类的目标是找到图的最小割（Min-Cut）。在数学上，这等价于求解 $L$ 的特征向量问题。

$$
f^T L f = \frac{1}{2} \sum_{i,j} W_{ij} (f_i - f_j)^2
$$

通过计算 $L$ 的前 $k$ 个最小特征值对应的特征向量，我们将原始的高维非线性数据映射到了一个低维的谱嵌入空间（Spectral Embedding Space）。

---

第六章：实战验证——几何与拓扑的对决

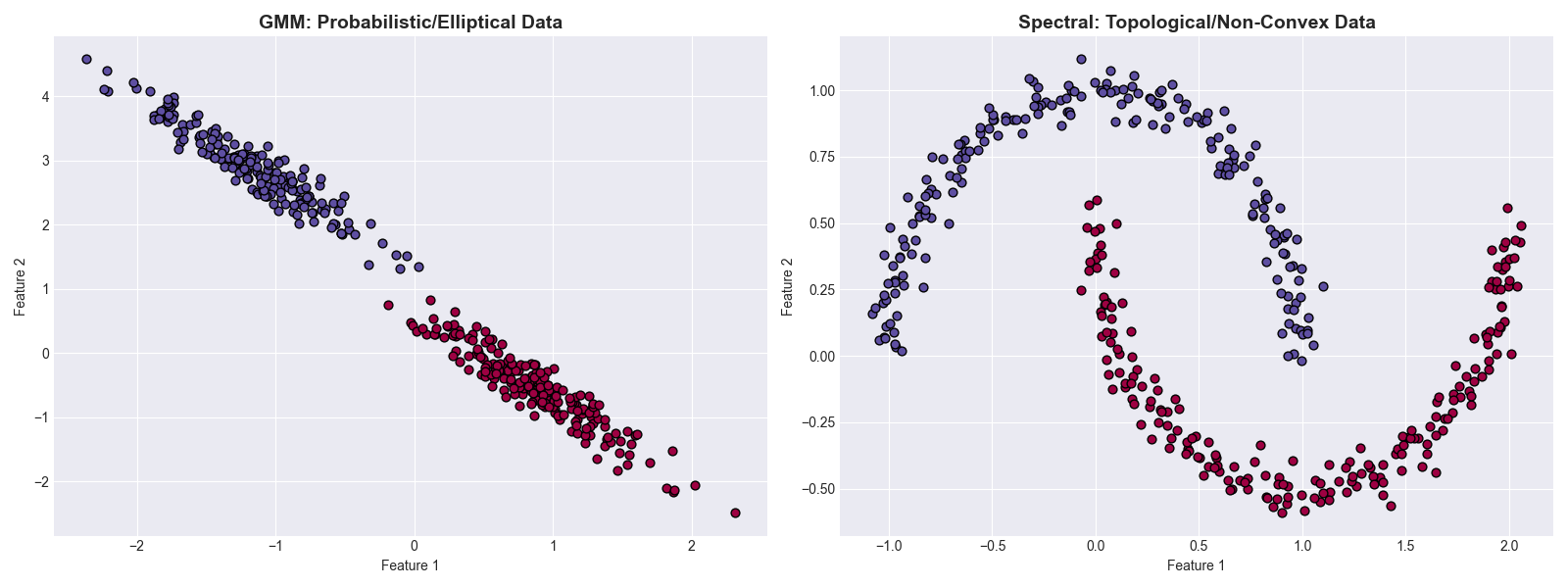
为了直观展示“概率分布（GMM）”与“拓扑结构（Spectral）”在处理不同数据形态时的本质差异，我们编写了以下完整的 Python 对比脚本。

这段代码将生成两种极端情况的数据：

1. 拉伸的椭圆数据：挑战欧氏距离（K-Means），适合 GMM。
2. 双月形非凸数据：挑战凸集假设，适合谱聚类。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs, make_moons
from sklearn.mixture import GaussianMixture
from sklearn.cluster import SpectralClustering

# 设置绘图风格
plt.style.use('seaborn-v0_8-darkgrid')


def plot_clustering(X, labels, title, subplot_index):
    """辅助函数：用于绘制聚类结果"""
    plt.subplot(1, 2, subplot_index)
    unique_labels = np.unique(labels)
    colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))

    for k, col in zip(unique_labels, colors):
        if k == -1:
            # 噪声点（如果算法支持）设为黑色
            col = [0, 0, 0, 1]

        class_member_mask = (labels == k)
        xy = X[class_member_mask]
        plt.scatter(xy[:, 0], xy[:, 1], c=[col], s=40, edgecolors='k', label=f'Cluster {k}')

    plt.title(title, fontsize=14, fontweight='bold')
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')


# ==========================================
# 场景 1: GMM (高斯混合模型) - 处理各向异性分布
# 第一性原理：数据由概率分布生成，且形状未必是正圆
# ==========================================

# 1. 生成拉伸的数据（模拟非球形分布，K-Means在此会失败）
X_gmm, y_gmm = make_blobs(n_samples=400, centers=2, cluster_std=0.60, random_state=0)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_gmm = np.dot(X_gmm, transformation)

# 2. 运行 GMM (covariance_type='full' 允许学习椭圆形状)
gmm = GaussianMixture(n_components=2, covariance_type='full', random_state=42)
gmm_labels = gmm.fit_predict(X_gmm)

# ==========================================
# 场景 2: Spectral Clustering (谱聚类) - 处理非凸结构
# 第一性原理：数据是图上的节点，聚类是切分图（连通性）
# ==========================================

# 1. 生成双月形数据（非凸，无法用直线分割）
X_spec, y_spec = make_moons(n_samples=400, noise=0.05, random_state=0)

# 2. 运行谱聚类 (affinity='nearest_neighbors' 构建近邻图)
spectral = SpectralClustering(
    n_clusters=2,
    eigen_solver='arpack',
    affinity="nearest_neighbors",
    n_neighbors=20,  # <--- 核心修改：增加近邻数，增强图的连通性
    random_state=42
)
spec_labels = spectral.fit_predict(X_spec)

# ==========================================
# 可视化对比
# ==========================================

plt.figure(figsize=(16, 6))
plot_clustering(X_gmm, gmm_labels, "GMM: Probabilistic/Elliptical Data", 1)
plot_clustering(X_spec, spec_labels, "Spectral: Topological/Non-Convex Data", 2)

plt.tight_layout()
plt.show()

代码解析

• 左图 (GMM): 成功捕捉到了被拉伸的椭圆分布。这是因为 GMM 的协方差矩阵 $\Sigma$ 学习到了数据的方向性，这是 K-Means 无法做到的。
• 右图 (Spectral): 成功分割了交错的双月形。这是因为算法构建了近邻图，识别出了数据在流形上的连通性，而非仅仅测量直线距离。
  

---

结论：寻找数据的“自然关节”

通过对 K-Means、GMM、DBSCAN 和谱聚类的解构，我们发现聚类算法的演进史，就是人类对“结构”这一概念理解不断深化的历史：

1. K-Means: 结构是空间中紧凑的球体（欧氏几何）。
2. GMM: 结构是统计分布的叠加（概率论）。
3. Spectral: 结构是图上的切分（谱图理论）。

在选择聚类算法时，我们不应仅仅关注计算效率，更应思考数据的物理生成过程（Data Generation Process）。聚类，最终是为了在信息的熵增海洋中，寻找那一抹低熵的孤岛。

---