拟牛顿法的巅峰：BFGS 算法详解与code实现

在深度学习彻底统治视野之前，数值优化领域曾有一座难以逾越的高峰，它就是 BFGS 算法 (Broyden–Fletcher–Goldfarb–Shanno algorithm)。

如果把梯度下降（Gradient Descent）比作一个只低头看路的登山者，那么牛顿法（Newton’s Method）就是一个拥有全地形地图的上帝。然而，上帝视角的代价是昂贵的——计算海森矩阵（Hessian Matrix）及其逆矩阵在工程上往往不可行。

BFGS 的伟大之处，在于它找到了一条完美的中间道路。它不需要直接计算那个昂贵的矩阵，而是通过观察每一步的“梯度变化”与“位移变化”，在迭代中逆向重构出地形的曲率信息。

它诞生于 1970 年，由四位数学家独立发现。在随后的几十年里，它是解决无约束非线性优化问题的标准答案。即使在今天，当我们需要极致的收敛精度而非单纯的统计平均时，BFGS 依然是那个不可替代的选择。

本文将剥离复杂的索引符号，从第一性原理出发，带你领略这个算法背后的数学直觉与几何之美。

一、 第一性原理：从牛顿法到 BFGS 的逻辑重构

要理解 BFGS，必须先理解它是如何“修补”牛顿法的。我们将把这个思维过程拆解为四个逻辑连贯的步骤。

1.1 起点：牛顿法的完美与代价

假设目标函数 $f(x)$ 是光滑的，我们在当前点 $x_k$ 处对其进行二阶泰勒展开：

$$
f(x) \approx f(x_k) + \nabla f(x_k)^T (x - x_k) + \frac{1}{2} (x - x_k)^T \mathbf{B} (x - x_k)
$$

这里 $\mathbf{B} = \nabla^2 f(x_k)$ 是真实的海森矩阵（Hessian Matrix），代表地形的曲率。
为了找到这个二次近似函数的极小值，我们对其求导并令其为 0，得到牛顿法的标准迭代公式：

$$
x_{k+1} = x_k - \mathbf{B}^{-1} \nabla f(x_k)
$$

这里的瓶颈在于：

1. 计算难：计算 $\mathbf{B}$ 需要 $O(N^2)$ 次二阶导数运算。
2. 求逆难：计算 $\mathbf{B}^{-1}$ 需要 $O(N^3)$ 的时间复杂度。当 $N$ 很大时，这是不可接受的。

BFGS 的核心思路：我们不再计算真实的 $\mathbf{B}$，也不直接求逆。我们要维护一个矩阵 $H_k$，用来直接近似 $\mathbf{B}^{-1}$（即海森矩阵的逆）。

1.2 观测：曲率蕴含在变化之中

如果不计算二阶导数，我们去哪里找曲率信息？答案在于：梯度的变化率。

想象你在爬山。

• 你迈出了一步：$s_k = x_{k+1} - x_k$ （位移）。
• 你发现脚下的坡度变了：$y_k = \nabla f(x_{k+1}) - \nabla f(x_k)$ （梯度的变化）。

根据梯度的泰勒展开（忽略高阶项）：
$$
\nabla f(x_{k+1}) \approx \nabla f(x_k) + \mathbf{B} \cdot (x_{k+1} - x_k)
$$

将 $s_k$ 和 $y_k$ 代入，我们得到：
$$
y_k \approx \mathbf{B} s_k
$$

因为我们要维护的是逆矩阵 $H_k \approx \mathbf{B}^{-1}$，所以我们在等式两边同乘 $H_{k+1}$，得到著名的拟牛顿条件（Quasi-Newton Condition），也称为割线方程：

$$
H_{k+1} y_k = s_k
$$

这个方程的物理含义极其深刻：更新后的矩阵 $H_{k+1}$，必须能够正确地将“梯度的变化 ($y_k$)”映射回“位移 ($s_k$)”。 这是任何拟牛顿法必须遵守的硬约束。

1.3 策略：最小的变化量

满足割线方程 $H_{k+1} y_k = s_k$ 的矩阵 $H_{k+1}$ 有无穷多个。BFGS 遵循**“最小作用量原理”**：我们希望新的矩阵 $H_{k+1}$ 与旧的矩阵 $H_k$ 尽可能相似，只做必要的修正。

这是一个带约束的优化问题：
$$
\min |H_{k+1} - H_k| \quad \text{s.t.} \quad H_{k+1} = H_{k+1}^T, \quad H_{k+1} y_k = s_k
$$

我们希望 $H_{k+1}$ 保持对称正定（保证下降方向），并满足割线方程。解决这个优化问题（利用加权 Frobenius 范数），我们最终推导出了 BFGS 更新公式。

1.4 结论：BFGS 更新公式

这就是我们在代码中实现的最终公式。它是一个秩二更新（Rank-Two Update），意味着我们在原矩阵上叠加了两个秩为 1 的修正项：

$$
H_{k+1} = (I - \rho_k s_k y_k^T) H_k (I - \rho_k y_k s_k^T) + \rho_k s_k s_k^T
$$

其中标量 $\rho_k = \frac{1}{y_k^T s_k}$。

二、 算法完整流程：盲人探险家的“心智地图”

为了理解 BFGS，请想象你被蒙住双眼放到了一个未知的山谷中。你的目标是找到海拔最低点。你手头有一个用来记录地形的“小本子”（矩阵 $H$），初始时它是空白的（单位矩阵）。

BFGS 的每一次迭代，就是一次完整的 “探测-行动-修正” 循环。

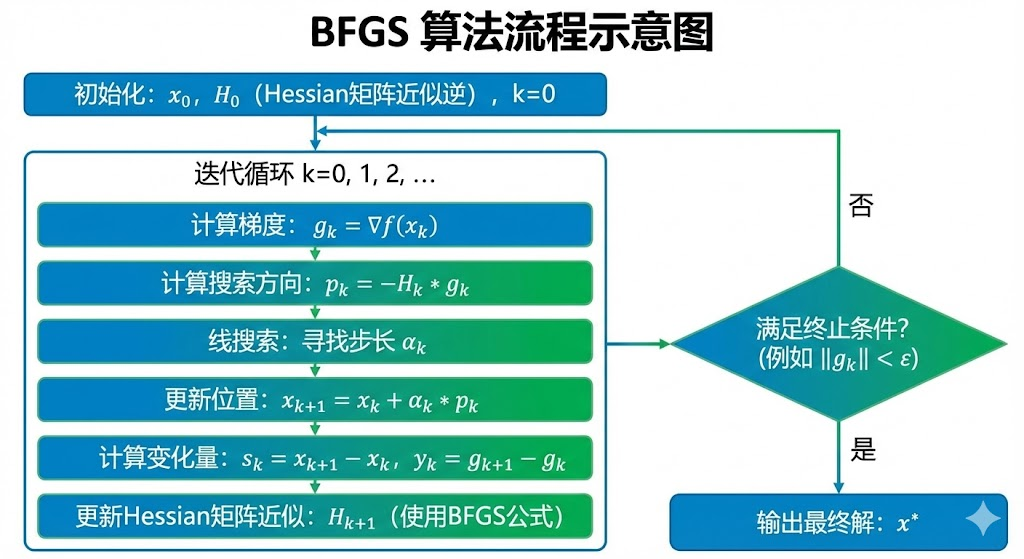
2.1 第一步：决定方向 (The Direction)

直觉：不要垂直切等高线，要切向谷底。

在当前位置 $x_k$，你的脚感觉到一个向下的坡度（梯度 $\nabla f$）。

• 梯度下降的做法：完全听从脚的感觉，垂直于等高线往下冲。这在狭长峡谷中会撞墙。
• BFGS 的做法：你会参考手中的“小本子” ($H_k$)。如果本子上记录着“这个方向虽然坡度大，但其实是峡谷壁，别往那走”，你会调整方向。

数学公式：
$$
p_k = -H_k \nabla f(x_k)
$$
这里的 $H_k$ 起到了 “扭转” 的作用，把梯度方向修正为直指谷底的方向。

2.2 第二步：试探步长 (Line Search)

直觉：步子太大容易扯着蛋，步子太小走不到终点。

选定方向 $p_k$ 后，你不能闭眼一直走。你需要决定走多远（步长 $\alpha_k$）。BFGS 要求步长必须满足两个 “安全规则” （Wolfe 条件）：

1. 必须要下降 (Armijo)：走完这一步，海拔必须确实降低了，不能白忙活。
2. 坡度要变缓 (Curvature)：如果你走到的新位置坡度还是很陡，说明你还没走到坑底，步子太小了；如果你走过了头导致坡度反向了，说明步子太大了。

在代码中，我们通常简化为一个回溯策略：先尝试迈一大步，如果发现没降下去，就退回来缩短一半，直到满足条件。

2.3 第三步：收集情报 (Information Gathering)

直觉：不仅看走了多远，还要看坡度变了多少。

你迈出了完美的一步，到达了新位置 $x_{k+1}$。现在你需要测量两样东西，这是更新地图的关键素材：

1. 位移 ($s_k$)：我实际移动了多少向量？
   $$s_k = x_{k+1} - x_k$$
2. 梯度差 ($y_k$)：坡度发生了什么变化？
   $$y_k = \nabla f(x_{k+1}) - \nabla f(x_k)$$

这两者的关系 ($H y_k = s_k$) 蕴含了这一段路程中地形的弯曲程度。

2.4 第四步：修正地图 (Matrix Update)

直觉：让小本子符合最新的观测结果。

这是 BFGS 的灵魂。利用 $s_k$ 和 $y_k$，我们对 $H_k$ 进行修正，得到 $H_{k+1}$。

但在修正前，必须做一个**“现实扭曲检查”**：
我们要检查 $y_k^T s_k > 0$。

• 含义：这表示当我们沿着位移方向走时，梯度是增加的（也就是地形是“凸”的，像个碗）。
• 保护机制：如果 $y_k^T s_k \le 0$，说明地形可能变成了“拱桥形”或者数据有误。强行更新会导致矩阵坏掉（不再正定），算法会崩溃。这时候 BFGS 会选择“装傻”，跳过这次更新，沿用旧地图。

如果检查通过，我们就套用那个吓人的秩二更新公式，将这一步获取的曲率信息永久刻入 $H$ 矩阵中。

---

总结：BFGS 的心路历程

1. 查地图：根据当前坡度和脑海中的地图，算出最佳方向。
2. 迈步子：小心翼翼地试探，直到找到一个既下降又平稳的落脚点。
3. 测变化：对比起步点和落脚点的坡度差异。
4. 改地图：“哦，原来这里比我想象的要陡/平！”，修正地图，准备下一步。

三、 完整的 Python 代码实现

为了彻底理解，我们将不使用 scipy.optimize，而是仅使用 numpy 实现 BFGS。代码包含测试函数（Rosenbrock）、回溯线搜索和 BFGS 主逻辑。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm


# ==========================================
# 1. 目标函数: Himmelblau Function
# ==========================================
def himmelblau(x):
    """
    Himmelblau 函数
    范围通常在 x, y ∈ [-5, 5]
    有 4 个全局最小点，函数值为 0
    """
    return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2


def himmelblau_grad(x):
    """
    Himmelblau 函数的梯度
    """
    term1 = x[0] ** 2 + x[1] - 11
    term2 = x[0] + x[1] ** 2 - 7

    grad = np.zeros_like(x)
    # 对 x 求导: 2 * term1 * 2x + 2 * term2 * 1
    grad[0] = 4 * x[0] * term1 + 2 * term2
    # 对 y 求导: 2 * term1 * 1 + 2 * term2 * 2y
    grad[1] = 2 * term1 + 4 * x[1] * term2
    return grad


# ==========================================
# 2. 优化算法 (保持核心逻辑不变)
# ==========================================
def backtracking_line_search(f, grad_f, x, p, alpha=1.0, rho=0.5, c=1e-4):
    f_val = f(x)
    grad_dot_p = np.dot(grad_f(x), p)
    current_alpha = alpha
    while f(x + current_alpha * p) > f_val + c * current_alpha * grad_dot_p:
        current_alpha *= rho
        if current_alpha < 1e-16: break
    return current_alpha


def gradient_descent(f, grad_f, x0, max_iter=1000, tol=1e-5):
    x = np.array(x0, dtype=float)
    path = [x.copy()]
    for k in range(max_iter):
        g = grad_f(x)
        if np.linalg.norm(g) < tol: break
        p = -g
        alpha = backtracking_line_search(f, grad_f, x, p)
        x = x + alpha * p
        path.append(x.copy())
    return x, np.array(path)


def bfgs_optimize(f, grad_f, x0, max_iter=200, tol=1e-5):
    x = np.array(x0, dtype=float)
    n = len(x)
    H = np.eye(n)
    path = [x.copy()]
    for k in range(max_iter):
        g = grad_f(x)
        if np.linalg.norm(g) < tol: break
        p = -np.dot(H, g)
        alpha = backtracking_line_search(f, grad_f, x, p)
        x_new = x + alpha * p
        s = x_new - x
        y = grad_f(x_new) - g
        rho_inv = np.dot(y, s)
        if rho_inv > 1e-10:
            rho = 1.0 / rho_inv
            I = np.eye(n)
            term1 = I - rho * np.outer(s, y)
            term2 = I - rho * np.outer(y, s)
            H = np.dot(term1, np.dot(H, term2)) + rho * np.outer(s, s)
        x = x_new
        path.append(x.copy())
    return x, np.array(path)


# ==========================================
# 3. 可视化逻辑 (针对 Himmelblau 调整)
# ==========================================
def plot_himmelblau_comparison(path_gd, path_bfgs):
    # 设定画图范围 [-5, 5] 是 Himmelblau 的经典展示区
    x = np.linspace(-5, 5, 400)
    y = np.linspace(-5, 5, 400)
    X, Y = np.meshgrid(x, y)

    # 这里的输入处理是为了适配 list 输入
    Z = (X ** 2 + Y - 11) ** 2 + (X + Y ** 2 - 7) ** 2

    plt.figure(figsize=(12, 10))

    # --- 1. 绘制伪彩热力图 ---
    # LogNorm 在这里非常重要，因为 Himmelblau 的最大值很大，但我们只关心 0 附近的细节
    # +0.1 是为了防止 log(0) 报错
    levels = np.logspace(-1, 3.5, 100)
    cp = plt.contourf(X, Y, Z + 0.1, levels=levels, cmap='viridis', norm=LogNorm())

    cbar = plt.colorbar(cp)
    cbar.set_label('Log Scale Objective Value', rotation=270, labelpad=20)

    # 叠加白色等高线增加层次感
    plt.contour(X, Y, Z, levels=levels[::5], colors='white', alpha=0.2, linewidths=0.5)

    # --- 2. 标记 4 个理论极小值点 ---
    minima = np.array([
        [3.0, 2.0],
        [-2.805118, 3.131312],
        [-3.779310, -3.283186],
        [3.584428, -1.848126]
    ])
    plt.scatter(minima[:, 0], minima[:, 1], s=100, facecolors='none', edgecolors='white',
                linewidth=2, linestyle='--', label='Global Minima (True)')

    # --- 3. 绘制算法路径 ---

    # Gradient Descent (白色虚线)
    plt.plot(path_gd[:, 0], path_gd[:, 1], color='white', linestyle='--', linewidth=1.5,
             label=f'Gradient Descent ({len(path_gd)} steps)')
    plt.scatter(path_gd[-1, 0], path_gd[-1, 1], color='white', s=50)

    # BFGS (红色实线)
    plt.plot(path_bfgs[:, 0], path_bfgs[:, 1], color='red', linestyle='-', linewidth=2.5,
             label=f'BFGS ({len(path_bfgs)} steps)')
    plt.scatter(path_bfgs[:, 0], path_bfgs[:, 1], color='red', s=50, zorder=10)

    # 标记起点
    plt.scatter(path_bfgs[0, 0], path_bfgs[0, 1], color='orange', marker='*', s=200,
                edgecolors='black', label='Start Point', zorder=20)

    plt.title('Himmelblau Function: 4 Minima Challenge\n(BFGS vs Gradient Descent)', fontsize=16)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend(loc='upper right', framealpha=0.8, facecolor='black', labelcolor='white')

    plt.tight_layout()
    plt.show()


# ==========================================
# 4. 运行
# ==========================================
if __name__ == "__main__":
    # 选取一个能够产生有趣路径的起始点
    # (0, 0) 在 Himmelblau 中是一个局部高点附近，算法需要决定往哪个坑里跳
    start_point = [0.0, 0.0]

    print(f"Start Point: {start_point}")

    _, path_gd = gradient_descent(himmelblau, himmelblau_grad, start_point)
    _, path_bfgs = bfgs_optimize(himmelblau, himmelblau_grad, start_point)

    print(f"GD Steps: {len(path_gd)}")
    print(f"BFGS Steps: {len(path_bfgs)}")

    plot_himmelblau_comparison(path_gd, path_bfgs)

运行结果如下图

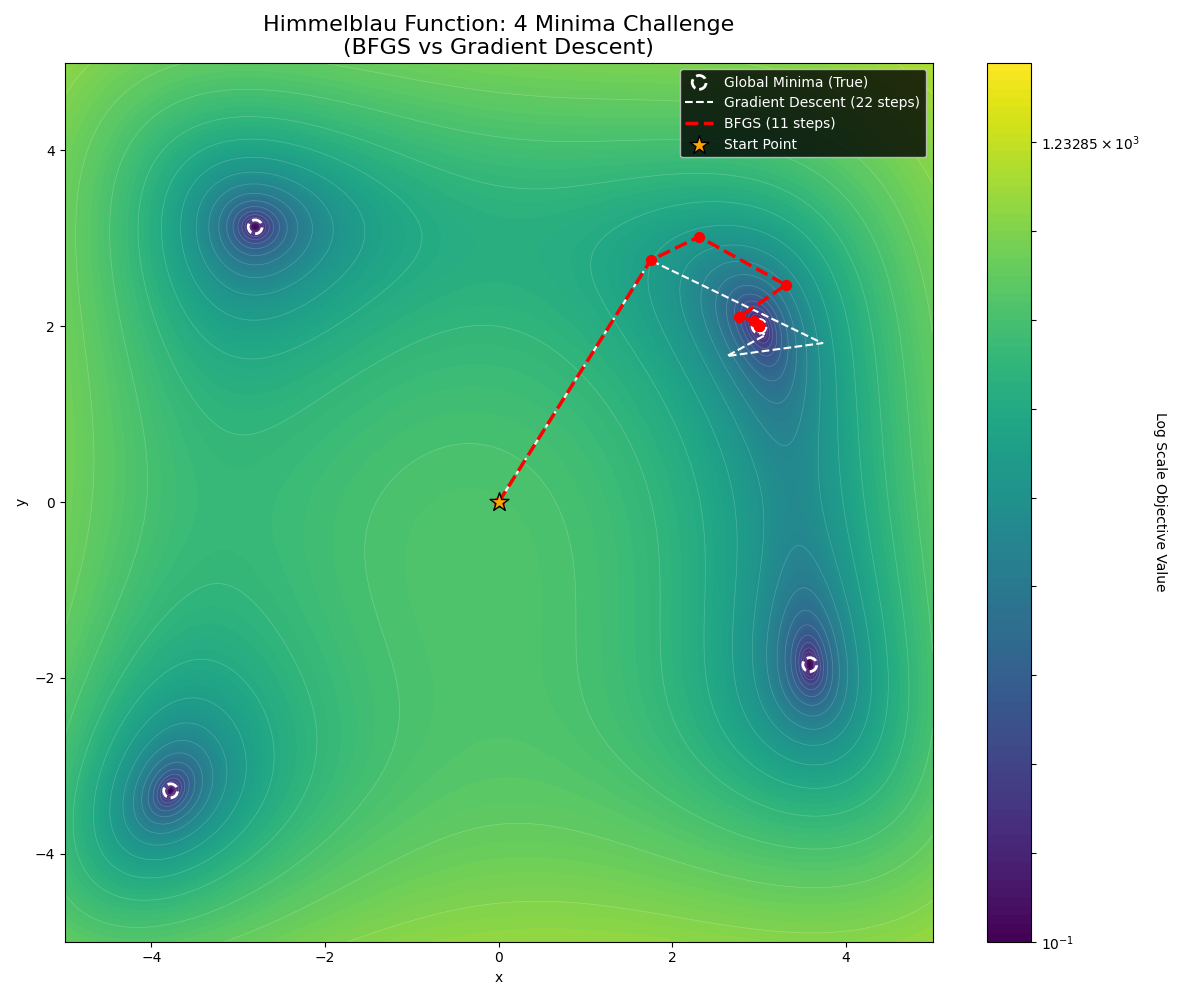
四、 深度解析：为什么 BFGS 优于梯度下降？

当你运行上述代码时，你会看到 BFGS 画出了一条优雅的弧线直奔终点，而梯度下降则在平坦区域寸步难行。这种巨大的性能鸿沟背后，隐藏着三个深刻的数学原理。

4.1 对抗“病态” (The Condition Number)

在 Beale 函数的平坦山谷中，Hessian 矩阵的条件数 (Condition Number) 非常大。

• 特征值差异：峡谷底部的特征值（对应平坦方向）非常小，而峡谷壁的特征值（对应陡峭方向）非常大。
• GD 的困境：梯度下降的收敛速度受制于 $\kappa = \lambda_{\max} / \lambda_{\min}$。为了不震荡，步长必须很小（受限于 $\lambda_{\max}$），但这导致它在平坦方向上（需要大步长）几乎不动。
• BFGS 的解法：BFGS 构建的矩阵 $H_k$ 本质上是在重新缩放坐标轴。它将那个狭长的椭圆峡谷，通过线性变换“拉圆”了。在一个正圆的势能面中，梯度方向就是指向圆心的方向，一步即可到达。

4.2 仿射不变性 (Affine Invariance)

这是牛顿法家族（包括 BFGS）最优雅的特性。
想象我们将变量 $x$ 的单位从“米”换成“毫米”，梯度下降是敏感的，你必须重新调整学习率。但 BFGS 是鲁棒的。无论你如何线性拉伸或旋转坐标系，BFGS 产生的迭代序列（在变换回原空间后）是完全一致的。这意味着 BFGS 自带归一化（Normalization）功能。

4.3 变度量视角 (Variable Metric Perspective)

在黎曼几何中，梯度下降是在欧几里得空间（Euclidean Space）中寻找最速下降方向，其隐含的度量矩阵是单位阵 $I$。
而 BFGS 实际上是在黎曼流形 (Riemannian Manifold) 上优化。矩阵 $H_k$ 定义了一个动态变化的度量张量 (Metric Tensor)：

$$
|x|_H = \sqrt{x^T H^{-1} x}
$$

BFGS 不仅仅是在跑，它还在不断地根据地形修改“距离”的定义。在平坦的方向上，它认为距离“很短”，所以敢迈大步；在陡峭的方向上，它认为距离“很长”，所以小心翼翼。

结语：在精确与效率之间

BFGS 算法并非真理的终点，而是一座精妙的桥梁。

四十多年前，Broyden, Fletcher, Goldfarb 和 Shanno 四位学者在计算资源极度匮乏的年代，通过对数学性质的极致挖掘，找到了一条能在“无知”（仅有一阶梯度）与“全知”（全海森矩阵）之间优雅穿行的路径。它教会我们的，不仅仅是计算公式，更是一种工程美学：

当我们无法承担追求完美的代价时，如何用最小的成本去逼近完美？

当然，BFGS 也有其时代的局限性。在参数量数以亿计、充满随机噪声的现代深度学习浪潮中，它往往不得不让位于更简单、更具统计鲁棒性的 SGD 及其变种。但每当我们回溯 L-BFGS 在大规模逻辑回归、条件随机场等经典模型中的贡献时，依然能感受到二阶优化思想的厚重。

学习 BFGS，与其说是为了掌握一种具体的工具，不如说是为了磨练一种 “见微知著” 的数学直觉——学会在只有局部信息的情况下，依然能描绘出全局的风景。

在算法的浩瀚海洋中，我们始终是探索者。保持谦逊，保持好奇，或许是我们面对未来不断变化的 AI 技术栈时，唯一不变的罗盘。