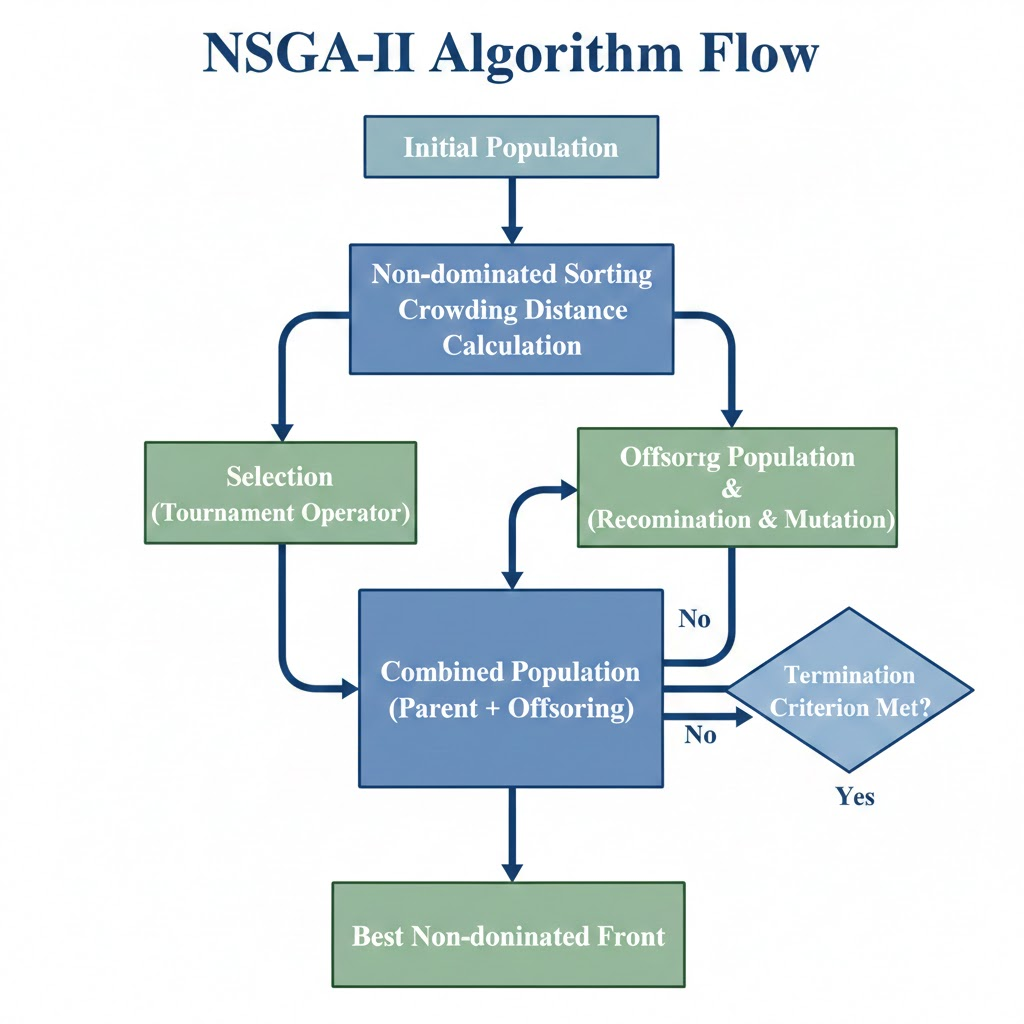
NSGA-II的原理解析及CODE实现

引言：权衡的哲学

在工程学、经济学乃至自然界的演化中，“最优”往往不是一个单一的极值，而是一组妥协。我们希望结构更轻但更强，投资回报更高但风险更低，神经网络精度更高但参数更少。

这些目标本质上是相互冲突的（Conflicting）。试图改善一个目标，往往意味着必须牺牲另一个目标。这种根本性的摩擦催生了 多目标优化（Multi-Objective Optimization, MOP） 的核心概念——帕累托最优（Pareto Optimality）。

与单目标优化寻找全局最小值不同，MOP 的目标是寻找一个解集——帕累托前沿（Pareto Front），代表了所有无法在不损害其他目标前提下改善某一目标的“完美权衡”状态。

本文将从第一性原理出发，解构该领域重要的里程碑：NSGA-II 。我们将探讨它们的设计哲学，数学基础，以及如何用代码实现它们。

NSGA-II的全称是 Non-dominated Sorting Genetic Algorithm II。中文通常翻译为：非支配排序遗传算法 II（或者第二代非支配排序遗传算法），它是由 K. Deb 等人在 2002 年提出的，是目前最流行、被引用次数最多的多目标进化算法之一。

第一部分：用直觉理解多目标优化

很多教程一上来就堆砌 $\mathbf{x} \in \Omega$ 和 $\nabla f(\mathbf{x})$，让人头大。我们不妨换个角度，把多目标优化想象成操作一个复杂的机器。

1.1 两个房间的故事：决策空间 vs. 目标空间

想象你在两个房间里工作，这两个房间通过一束看不见的电缆连接。

  • 房间 A（决策空间 Decision Space）：
    这里有一个巨大的控制台，上面有许多旋钮和推杆。

    • 旋钮可能是：“机翼长度”、“材料厚度”、“发动机喷油量”。
    • 你的每一个操作（一组旋钮的刻度），就是一个“解”，记为 $\mathbf{x}$。

  • 房间 B（目标空间 Objective Space）：
    这里没有旋钮，只有墙上的几个显示屏。

    • 屏幕显示着：“飞行速度”、“耗油量”、“制造成本”。
    • 屏幕上的数值，就是优化的“结果”，记为 $\mathbf{y}$。

关键难点：非线性映射
问题在于，这两个房间的关系是非常扭曲的。
你把“材料厚度”旋钮往右拧一点（决策空间微小变化），房间 B 里的“制造成本”可能猛增，而“安全性”却只增加了一点点。甚至，可能存在某种共振，稍微动一下旋钮，结果就天翻地覆。
NSGA 算法的工作，就是在这个黑盒子里，通过不断尝试拧旋钮，试图画出房间 B 里那些屏幕能达到的极限数值边界。

1.2 为什么会有冲突？（气球理论）

如果所有屏幕的数值能同时变好（速度越快、油耗越低、成本越低），那就不需要多目标优化了，只需要拼命拧旋钮就行。

但在现实中，这就像捏一个充满了水的气球。

  • 你按下“成本”这一侧（试图降低成本），气球的另一侧“性能”就会鼓起来（性能变差）。
  • 你按下“油耗”这一侧，另一侧“动力”就会鼓起来。

帕累托最优（Pareto Optimality） 的状态，就是你把这个气球压缩到了极限。再想按下去任何一点，其他地方就一定会鼓出来。这种“按不下去”的状态，就是我们要找的解。

1.3 帕累托支配：一种“无需纠结”的比较

在单目标世界里，5 比 3 大，这很简单。但在多目标世界里，怎么比大小？
我们用**“买车”来理解支配（Dominance）**。

假设我们要买车，只看两个指标：价格（越低越好） 和 速度（越快越好）。

情况一：完全碾压（支配 Dominance）

  • 车 A： 10万，最高时速 200 km/h。
  • 车 B： 15万，最高时速 150 km/h。

这里，车 A 此时就是 “支配” 了车 B。

  • 价格：A 比 B 便宜（A 赢）。
  • 速度：A 比 B 快（A 赢）。
    结论： 理性人绝对不会买车 B。车 B 是劣质解，直接淘汰。

情况二：两难选择（互不支配 Non-dominated）

  • 车 A： 10万，最高时速 200 km/h。
  • 车 C： 8万，最高时速 180 km/h。

这就纠结了。

  • 比价格？C 赢。
  • 比速度？A 赢。
    结论： A 和 C 互有胜负，谁也没法完全碾压谁。这时候，A 和 C 就是 “互不支配” 的。

NSGA 的目标：
找到一大堆像 A 和 C 这样“互不支配”的解，把那些像 B 一样被碾压的解全部扔掉。这一堆留下的解，连成一条线，就是帕累托前沿（Pareto Front）。

1.4 高维度的诅咒：当每个人都是冠军

NSGA-II 在处理 2 个或 3 个目标时很强，但为什么到了 4 个甚至 10 个目标（高维）时就失效了？

想象一个 100 人的班级。

  • 如果只比“数学成绩”： 第一名只有一个，很容易排序。
  • 如果比 10 个科目（数学、语文、体育、音乐、绘画…）：

在多目标的高维空间里，每个人都能找到自己“赢”的那个点。

  • 小明：虽然我数学差，但我体育好啊！（没被支配）
  • 小红：虽然我体育差，但我唱歌好啊！（没被支配）
  • 小强：虽然我啥都不行，但我打游戏第一啊！（没被支配）

结果就是： 在高维空间里，几乎所有解都是“互不支配”的。大家都在第一梯队（Rank 1）。
这时候，NSGA-II 的排序机制就失效了——因为它分不出谁更好。这就是为什么我们需要 NSGA-III，它不再单纯依赖“谁支配谁”，而是引入了“参考点”（Reference Points），像插旗子一样，强行在各个方向上保留最好的代表。这篇文章就不做展开介绍。

1.5 进化图谱：从 GA 到 NSGA 的血缘与革新

在深入 NSGA-II 的算法细节之前，我们必须先厘清它与标准遗传算法（Genetic Algorithm, GA）之间千丝万缕的联系。很多初学者误以为 NSGA 是一种全新的算法，但从第一性原理来看，NSGA 本质上是 GA 在多维空间的一种“特化变体”。

我们可以通过 “继承（Inheritance）” 和 “重构（Refactoring）” 这两个维度来解构它们的关系。

1.5.1 继承：不变的驱动引擎

如果把算法比作一辆赛车，那么 GA 和 NSGA 使用的是完全相同的底盘和引擎。这意味着，驱动种群在决策空间中进行“探索（Exploration）”和“开发（Exploitation）”的生物学算子并未发生改变。

  • 编码方式 (Encoding): 无论是单目标的 GA 还是多目标的 NSGA，解的表示方法是一样的。对于连续优化问题，它们都使用实数编码；对于离散问题，都使用二进制或排列编码。
  • 搜索算子 (Search Operators): 这是进化的动力源。
    • 交叉 (Crossover): 如模拟二进制交叉 (SBX)。它的作用是混合父代基因，产生新的可能性。
    • 变异 (Mutation): 如多项式变异 (Polynomial Mutation)。它的作用是随机扰动，防止算法陷入局部最优。

结论： 你在标准 GA 中学到的关于“如何产生新解”的知识，在 NSGA 中完全通用。

1.5.2 重构：评价机制的范式转移

GA 和 NSGA 的分道扬镳，发生在**“自然选择”**这一步。

  • 标准 GA 的逻辑（标量霸权）：
    在单目标世界里，上帝是简单的。对于任意两个个体 $A$ 和 $B$，要么 $f(A) < f(B)$，要么 $f(A) > f(B)$。GA 只需要根据这个标量适应度（Fitness），使用轮盘赌或锦标赛选择，就能轻松决定谁该活下来。

  • NSGA 的困境（向量迷局）：
    在多目标世界里，个体 $A$ 的得分为 $[10, 80]$，个体 $B$ 的得分为 $[20, 60]$。谁更好？GA 的标量比较逻辑失效了。如果你强行把它们加权求和（例如 $0.5f_1 + 0.5f_2$），你就把多目标退化回了单目标，这违背了寻找“多样化权衡解”的初衷。

  • NSGA 的解决方案（虚拟适应度）：
    NSGA 没有改变 GA 的框架，而是重写了 evaluate() 和 select() 函数。它引入了一套**“虚拟适应度”**体系：

    1. 等级 (Rank): 既然无法直接比大小，那就比“谁支配谁”。非支配排序将种群分层，Rank 1 的个体被视为“最强”。
    2. 拥挤度 (Distance): 在同等级别下，谁周围更空旷，谁的基因就更有保留价值（为了维持多样性）。

1.5.3 核心差异对比表

特性 标准 GA (Standard GA) NSGA-II
优化目标 单一目标函数 $\min f(x)$ 目标向量 $\min \mathbf{F}(x)$
比较逻辑 标量比较 (Scalar Comparison) 帕累托支配 (Pareto Dominance)
适应度定义 直接等于目标函数值 (或其变换) Rank (收敛性) + Crowding Distance (分布性)
选择压力 优胜劣汰，只保留 $f(x)$ 最好的 分层淘汰，保留前沿面并维持稀疏分布
最终产出 全局最优解 (Global Optimum) 帕累托最优解集 (Pareto Optimal Set)

总结：
NSGA-II 并没有发明新的进化方式，它只是给传统的 GA 换了一个更聪明的“导航员”。这个导航员不再执着于寻找“唯一的王”，而是指挥种群去占领那条漫长而复杂的帕累托前沿防线。

第二部分：NSGA-II原理介绍

Deb 等人在 2002 年提出的 NSGA-II 是进化计算领域的经典。它主要解决了初代 NSGA 的计算复杂度高、缺乏精英策略（Elitism）以及需要手动指定共享参数的问题。NSGA-II 建立在三大支柱之上：

  1. 快速非支配排序 (Fast Non-dominated Sorting): 建立收敛压力。
  2. 拥挤距离 (Crowding Distance): 维持种群多样性，无需参数。
  3. 精英保留策略 (Elitism): 防止优秀解在进化中丢失。

2.1 核心机制一：快速非支配排序 (The “Onion Peeling” Strategy)

想象一堆散落在桌子上的豆子（种群个体）。有些豆子在所有方面都比别的豆子大（支配），有些则互有胜负。
NSGA-II 的排序过程，就像是 “剥洋葱”。

步骤演示：

  1. 寻找第一层（Pareto Front 1）：
    找出所有“没有任何人能支配我”的豆子。把它们挑出来，放在一边，标记为 Rank 1（第一梯队）。这是目前最好的解集。

  2. 寻找第二层（Pareto Front 2）：
    假设刚才拿走的 Rank 1 豆子都不存在了。在剩下的豆子里，再次寻找“没有任何人能支配我”的豆子。标记为 Rank 2。
    注意：Rank 2 的豆子实际上是被 Rank 1 支配的，但在剩余的豆子里它们是最强的。

  3. 重复剥离：
    不断重复这个过程，直到所有豆子都被分了等级（Rank 1, Rank 2, Rank 3…）。

算法实现的技巧（$O(N^2)$）

为了不让计算机算死（初代 NSGA 复杂度高达 $O(N^3)$），NSGA-II 采用了一个聪明的记账本策略：

  • 支配计数 ($n_p$)： 每个人记一个小本本，写上“有多少人比我强”。如果 $n_p=0$，说明没人比我强，我就是 Rank 1。
  • 被支配集合 ($S_p$)： 每个人再记一个名单，写上“我比哪些人强”。

剥皮逻辑：

  1. 先把所有 $n_p=0$ 的人请出列，归入当前 Front。
  2. 这些人离开时，通知他们名单 $S_p$ 里的所有人：“霸主走了，你们的 $n_p$ 减 1”。
  3. 如果某人的 $n_p$ 减到了 0，说明压在他头上的大山都没了，他晋升为下一层的霸主，加入 Next Front。

2.2 核心机制二：拥挤距离 (The “Social Distancing” Strategy)

如果只按 Rank 排序，大家都会争抢帕累托前沿中间那段最容易达到的位置，导致解集分布不均匀。
NSGA-II 引入了 拥挤距离（Crowding Distance），鼓励大家**“保持社交距离”**。

计算逻辑：

对于同一层级（同 Rank）的个体：

  1. 端点奖励： 处于极值点（比如最便宜的车、最快的车）的个体，距离设为无穷大 $\infty$。我们永远想保留探索边界的人。
  2. 中间计算： 对于中间的个体，它的拥挤距离等于它在所有目标维度上的“前后邻居”构成的长方体的周长。

$$
d_i = \sum_{m=1}^{M} \frac{f_m(i+1) - f_m(i-1)}{f_m^{max} - f_m^{min}}
$$

  • 直观理解： 你的拥挤距离越大，说明你周围越空旷，你的存在越独特（稀缺资源）。
  • 选择策略： 当两辆车 Rank 相同时，选那个周围没人的车（拥挤距离大的）。

2.3 精英保留的主循环 (Elitism Loop)

NSGA-II 的进化过程是一场残酷的 “父子混合大乱斗”。

常规遗传算法通常是用子代直接覆盖父代。但 NSGA-II 认为：如果老父亲比儿子强，就应该保留父亲。

流程图解：

  1. 父代 ($P_t$) + 子代 ($Q_t$) = 混合种群 ($R_t$)。
    如果种群大小是 $N$，现在我们就有了 $2N$ 个个体。
  2. 全体排序： 对这 $2N$ 个个体进行“洋葱剥皮”分层。
  3. 填装新一代：
    • 先把 Rank 1 的全部放入新种群。
    • 如果没满，再把 Rank 2 的全部放入。
    • …
    • 临界层截断（关键）： 假设放到 Rank 3 时，位置不够了。这时候，只在 Rank 3 内部，按照拥挤距离从大到小排序，把前几名塞进去，填满 $N$ 个位置为止。剩下的全部淘汰。

第三部分 Code实现

3.1 Matlab code实现

运行结果如图

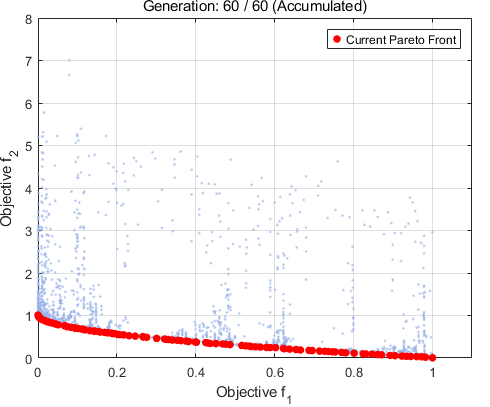
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
clc; clear; close all;

% --- 1. 参数设置 ---
pop_size = 100;
max_gen = 60;
n_vars = 30;
bounds = [0, 1];

fprintf('启动轨迹模式 (Pop: %d, Gen: %d)...\n', pop_size, max_gen);

% --- 2. 初始化 ---
empty_individual.pos = [];
empty_individual.cost = [];
empty_individual.rank = [];
empty_individual.dist = [];
pop = repmat(empty_individual, pop_size, 1);

for i = 1:pop_size
    pop(i).pos = unifrnd(bounds(1), bounds(2), [1, n_vars]);
    pop(i).cost = zdt1(pop(i).pos);
end

% --- 3. 绘图设置 ---
figure('Name', 'NSGA-II Search Trajectory', 'Color', 'w');
ax = gca;
hold(ax, 'on');
grid(ax, 'on');
box(ax, 'on');

xlim([0, 1.1]);
ylim([0, 8.0]);
xlabel('Objective f_1');
ylabel('Objective f_2');
title_handle = title('Initializing...');

% 创建用于图例的红色前沿句柄
h_best_front = plot(ax, NaN, NaN, 'o', ...
    'MarkerEdgeColor', 'r', ...
    'MarkerFaceColor', 'r', ...
    'MarkerSize', 5, 'DisplayName', 'Current Pareto Front');

% --- 关键修改：明确指定图例只显示这一个句柄 ---
legend(ax, h_best_front, 'Location', 'northeast');

% --- 4. 主循环 ---
for gen = 1:max_gen

    costs = vertcat(pop.cost);
    [pop, fronts] = NonDominatedSorting(pop);
    pop = CalcCrowdingDistance(pop, fronts);

    % === 绘图核心逻辑 (已修复) ===

    % 1. 画下当前种群的"足迹"
    % ---【修复】添加 'HandleVisibility', 'off' ---
    % 这会让图例彻底忽略这些点
    plot(ax, costs(:,1), costs(:,2), '.', ...
        'Color', [0.6 0.7 0.9], ...
        'MarkerSize', 4, ...
        'HandleVisibility', 'off');

    % 2. 更新红色的前沿
    front_costs = costs(fronts{1}, :);
    set(h_best_front, 'XData', front_costs(:,1), 'YData', front_costs(:,2));

    % 确保红色前沿始终在最上层
    uistack(h_best_front, 'top');

    set(title_handle, 'String', sprintf('Generation: %d / %d (Accumulated)', gen, max_gen));

    drawnow;

    % === 进化操作 ===
    offspring = GenerateOffspring(pop, bounds);
    merged_pop = [pop; offspring];
    [merged_pop, fronts] = NonDominatedSorting(merged_pop);
    merged_pop = CalcCrowdingDistance(merged_pop, fronts);

    new_pop = [];
    front_idx = 1;
    while length(new_pop) + length(fronts{front_idx}) <= pop_size
        new_pop = [new_pop; merged_pop(fronts{front_idx})];
        front_idx = front_idx + 1;
    end
    remaining = pop_size - length(new_pop);
    if remaining > 0
        last_front = merged_pop(fronts{front_idx});
        [~, sorted_idx] = sort([last_front.dist], 'descend');
        new_pop = [new_pop; last_front(sorted_idx(1:remaining))];
    end
    pop = new_pop;
end

fprintf('完成。\n');


% --- 辅助函数保持不变，为节省篇幅省略，请使用上一段代码中的辅助函数 ---
% zdt1, NonDominatedSorting, CalcCrowdingDistance, GenerateOffspring...
% (请确保运行前这里包含了那些函数，或者它们在同一个文件里)
% -----------------------------------------------------------

% (为方便您直接复制运行，这里补全必要的辅助函数)
function z = zdt1(x)
f1 = x(1);
g = 1 + 9 * mean(x(2:end));
h = 1 - sqrt(f1/g);
f2 = g * h;
z = [f1, f2];
end

function [pop, fronts] = NonDominatedSorting(pop)
N = length(pop);
costs = vertcat(pop.cost);
for i=1:N
    pop(i).n = 0; pop(i).S = [];
end
fronts = {[]};
for p=1:N
    for q=1:N
        if all(costs(p,:)<=costs(q,:)) && any(costs(p,:)<costs(q,:))
            pop(p).S = [pop(p).S q];
        elseif all(costs(q,:)<=costs(p,:)) && any(costs(q,:)<costs(p,:))
            pop(p).n = pop(p).n + 1;
        end
    end
    if pop(p).n == 0; pop(p).rank = 1; fronts{1} = [fronts{1} p]; end
end
i=1;
while ~isempty(fronts{i})
    Q = [];
    for p = fronts{i}
        for q = pop(p).S
            pop(q).n = pop(q).n - 1;
            if pop(q).n == 0; pop(q).rank = i+1; Q = [Q q]; end
        end
    end
    i=i+1; fronts{i} = Q;
end
fronts(end) = [];
end

function pop = CalcCrowdingDistance(pop, fronts)
n_obj = length(pop(1).cost);
costs = vertcat(pop.cost);
for i=1:length(pop); pop(i).dist = 0; end
for f = 1:length(fronts)
    idx = fronts{f};
    if length(idx)<2; [pop(idx).dist] = deal(inf); continue; end
    for m = 1:n_obj
        [sorted, map] = sort(costs(idx, m));
        sorted_idx = idx(map);
        pop(sorted_idx(1)).dist = inf; pop(sorted_idx(end)).dist = inf;
        d_range = sorted(end)-sorted(1);
        if d_range == 0; continue; end
        for k=2:length(idx)-1
            pop(sorted_idx(k)).dist = pop(sorted_idx(k)).dist + (sorted(k+1)-sorted(k-1))/d_range;
        end
    end
end
end

function offspring = GenerateOffspring(pop, bounds)
pop_size = length(pop);
n_vars = length(pop(1).pos);
offspring = repmat(pop(1), pop_size, 1);
eta_c = 20; pc = 0.9; eta_m = 20; pm = 1/n_vars;
for k = 1:2:pop_size
    p1 = Tournament(pop); p2 = Tournament(pop);
    c1 = p1.pos; c2 = p2.pos;
    if rand <= pc
        [c1, c2] = SBX(p1.pos, p2.pos, bounds, eta_c);
    end
    offspring(k).pos = Mut(c1, bounds, pm, eta_m);
    offspring(k).cost = zdt1(offspring(k).pos);
    offspring(k+1).pos = Mut(c2, bounds, pm, eta_m);
    offspring(k+1).cost = zdt1(offspring(k+1).pos);
end
end

function best = Tournament(pop)
i = randsample(length(pop), 2);
p1 = pop(i(1)); p2 = pop(i(2));
if p1.rank < p2.rank; best = p1;
elseif p2.rank < p1.rank; best = p2;
elseif p1.dist > p2.dist; best = p1;
else; best = p2; end
end

function [c1, c2] = SBX(p1, p2, b, eta)
rand_val = rand(size(p1));
c1=p1; c2=p2;
idx = rand_val <= 0.5 & abs(p1-p2)>1e-10;
if any(idx)
    y1=min(p1(idx),p2(idx)); y2=max(p1(idx),p2(idx));
    beta = 1.0 + (2.0*(y1-b(1))./(y2-y1));
    alpha = 2.0 - beta.^(-(eta+1));
    r = rand(1, sum(idx));
    bq = (r.*alpha).^(1/(eta+1));
    mask = r > (1./alpha);
    bq(mask) = (1./(2-r(mask).*alpha(mask))).^(1/(eta+1));
    c1(idx) = 0.5*((y1+y2)-bq.*(y2-y1));
    c2(idx) = 0.5*((y1+y2)+bq.*(y2-y1));
end
c1 = max(min(c1, b(2)), b(1));
c2 = max(min(c2, b(2)), b(1));
end

function x = Mut(x, b, pm, eta)
idx = rand(size(x)) <= pm;
if any(idx)
    y = x(idx);
    d1 = (y-b(1))/(b(2)-b(1)); d2 = (b(2)-y)/(b(2)-b(1));
    r = rand(1, sum(idx));
    dq = (2*r + (1-2*r).*(1-d1).^(eta+1)).^(1/(eta+1)) - 1;
    mask = r > 0.5;
    dq(mask) = 1 - (2*(1-r(mask)) + 2*(r(mask)-0.5).*(1-d2(mask)).^(eta+1)).^(1/(eta+1));
    x(idx) = y + dq.*(b(2)-b(1));
end
x = max(min(x, b(2)), b(1));
end

3.2 Python code实现

运行结果如图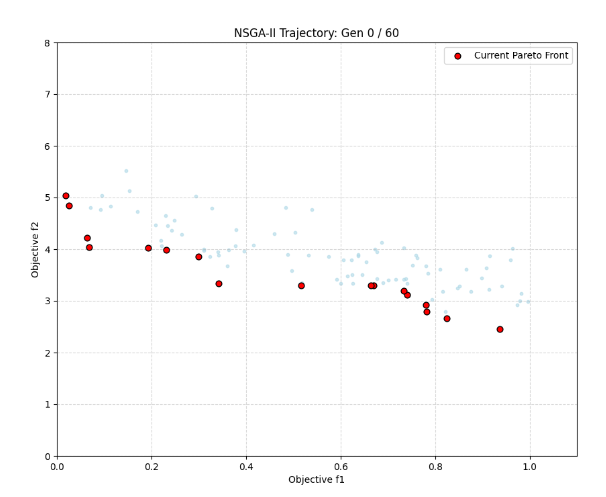

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
import numpy as np
import matplotlib.pyplot as plt


# ==========================
# 1. 问题定义 (ZDT1)
# ==========================
def zdt1(x):
    """ZDT1 测试函数 (支持向量化计算)"""
    # x shape: (pop_size, n_var)
    if x.ndim == 1:
        x = x.reshape(1, -1)

    n_point, n_var = x.shape
    f1 = x[:, 0]
    g = 1 + 9 * np.sum(x[:, 1:], axis=1) / (n_var - 1)
    h = 1 - np.sqrt(f1 / g)
    f2 = g * h
    return np.column_stack([f1, f2])


# ==========================
# 2. 核心算法组件
# ==========================
def fast_non_dominated_sort(values):
    """快速非支配排序"""
    num_pop = values.shape[0]
    S = [[] for _ in range(num_pop)]
    front = [[]]
    n = np.zeros(num_pop, dtype=int)
    rank = np.zeros(num_pop, dtype=int)

    # 支配关系矩阵计算 (利用广播加速)
    # dominates[i, j] = True 表示 i 支配 j
    val_expanded_1 = values[:, np.newaxis, :]
    val_expanded_2 = values[np.newaxis, :, :]

    # 严格更优
    better = (val_expanded_1 <= val_expanded_2).all(axis=2) & (val_expanded_1 < val_expanded_2).any(axis=2)

    for p in range(num_pop):
        # p 支配的解的索引
        S[p] = np.where(better[p])[0].tolist()
        # 支配 p 的解的数量
        n[p] = np.sum(better[:, p])

        if n[p] == 0:
            rank[p] = 0
            front[0].append(p)

    i = 0
    while front[i]:
        Q = []
        for p in front[i]:
            for q in S[p]:
                n[q] -= 1
                if n[q] == 0:
                    rank[q] = i + 1
                    Q.append(q)
        i += 1
        front.append(Q)

    del front[len(front) - 1]
    return front


def crowding_distance_assignment(values, front):
    """拥挤距离计算"""
    l = len(front)
    distance = np.zeros(l)
    if l == 0: return distance

    num_obj = values.shape[1]
    front_obj = values[front]

    for m in range(num_obj):
        # 对当前目标进行排序
        sorted_idx = np.argsort(front_obj[:, m])
        front_obj_sorted = front_obj[sorted_idx]

        # 边界点设为无穷大
        distance[sorted_idx[0]] = np.inf
        distance[sorted_idx[-1]] = np.inf

        f_min = front_obj_sorted[0, m]
        f_max = front_obj_sorted[-1, m]

        if np.isclose(f_max, f_min):
            continue

        # 累加距离
        norm = f_max - f_min
        distance[sorted_idx[1:-1]] += (front_obj_sorted[2:, m] - front_obj_sorted[:-2, m]) / norm

    # 将局部 distance 映射回原始 front 的顺序 (为了方便外部调用，其实可以直接返回 dict)
    # 但这里我们返回对应 front 索引的距离列表
    return distance


# ==========================
# 3. 遗传算子
# ==========================
def tournament_selection(pop, rank, distance, k=2):
    n_pop = len(pop)
    selected_indices = []

    # 向量化锦标赛选择的准备
    participants = np.random.choice(n_pop, (n_pop, k))

    for i in range(n_pop):
        candidates = participants[i]
        best = candidates[0]
        for idx in candidates[1:]:
            # 比较逻辑: Rank越小越好; Rank相同时 Distance越大越好
            if rank[idx] < rank[best]:
                best = idx
            elif rank[idx] == rank[best] and distance[idx] > distance[best]:
                best = idx
        selected_indices.append(best)

    return pop[selected_indices]


def crossover_mutation(pop, lower_bound, upper_bound, pc=0.9, pm=1.0 / 30, eta_c=20, eta_m=20):
    n_pop, n_var = pop.shape
    offspring = np.zeros_like(pop)

    # SBX Crossover
    for i in range(0, n_pop, 2):
        p1, p2 = pop[i], pop[i + 1]
        if np.random.rand() < pc:
            c1, c2 = np.copy(p1), np.copy(p2)
            rand_vals = np.random.rand(n_var)

            # 只有满足条件的维度才交叉
            mask = np.random.rand(n_var) <= 0.5

            if np.any(mask):
                y1 = np.minimum(p1, p2)
                y2 = np.maximum(p1, p2)

                beta = 1.0 + (2.0 * (y1 - lower_bound) / (y2 - y1 + 1e-10))
                alpha = 2.0 - np.power(beta, -(eta_c + 1.0))

                beta_q = np.zeros(n_var)
                mask_lower = rand_vals <= (1.0 / alpha)

                val_lower = np.power(rand_vals * alpha, 1.0 / (eta_c + 1.0))
                val_upper = np.power(1.0 / (2.0 - rand_vals * alpha), 1.0 / (eta_c + 1.0))

                beta_q[mask_lower] = val_lower[mask_lower]
                beta_q[~mask_lower] = val_upper[~mask_lower]

                # 应用只在 mask 为 True 的位置
                c1[mask] = 0.5 * ((y1[mask] + y2[mask]) - beta_q[mask] * (y2[mask] - y1[mask]))
                c2[mask] = 0.5 * ((y1[mask] + y2[mask]) + beta_q[mask] * (y2[mask] - y1[mask]))

            offspring[i] = np.clip(c1, lower_bound, upper_bound)
            offspring[i + 1] = np.clip(c2, lower_bound, upper_bound)
        else:
            offspring[i], offspring[i + 1] = p1, p2

    # Polynomial Mutation
    mutation_mask = np.random.rand(n_pop, n_var) < pm
    if np.any(mutation_mask):
        y = offspring[mutation_mask]
        delta_1 = (y - lower_bound) / (upper_bound - lower_bound)
        delta_2 = (upper_bound - y) / (upper_bound - lower_bound)

        rand_vals = np.random.rand(len(y))
        mut_pow = 1.0 / (eta_m + 1.0)

        delta_q = np.zeros(len(y))
        mask_lower = rand_vals <= 0.5

        val_lower = np.power(2.0 * rand_vals + (1.0 - 2.0 * rand_vals) * np.power(1.0 - delta_1, eta_m + 1.0),
                             mut_pow) - 1.0
        val_upper = 1.0 - np.power(
            2.0 * (1.0 - rand_vals) + 2.0 * (rand_vals - 0.5) * np.power(1.0 - delta_2, eta_m + 1.0), mut_pow)

        delta_q[mask_lower] = val_lower[mask_lower]
        delta_q[~mask_lower] = val_upper[~mask_lower]

        offspring[mutation_mask] = np.clip(y + delta_q * (upper_bound - lower_bound), lower_bound, upper_bound)

    return offspring


# ==========================
# 4. 主程序 (Trace Mode Visualization)
# ==========================
def main():
    # 参数设置
    POP_SIZE = 100
    MAX_GEN = 60
    N_VAR = 30
    BOUNDS = [0, 1]

    # 初始化
    pop = np.random.uniform(BOUNDS[0], BOUNDS[1], (POP_SIZE, N_VAR))

    print(f"启动 Python NSGA-II 轨迹可视化 (Pop: {POP_SIZE}, Gen: {MAX_GEN})")

    # === 绘图初始化 ===
    plt.ion()
    fig, ax = plt.subplots(figsize=(10, 8))

    # 1. 设置坐标轴范围 (防止画面抖动)
    ax.set_xlim(0, 1.1)
    ax.set_ylim(0, 8.0)
    ax.set_xlabel('Objective f1')
    ax.set_ylabel('Objective f2')
    ax.set_title('NSGA-II Search Trajectory')
    ax.grid(True, linestyle='--', alpha=0.5)

    # 2. 创建红色前沿的占位对象 (高层级 zorder=10)
    # 注意：这里我们只创建一个 label，后续的蓝色点都不会有 label
    sc_best_front = ax.scatter([], [], c='red', s=40, edgecolors='black', zorder=10, label='Current Pareto Front')

    # 3. 只需要显示这个唯一的 label
    ax.legend(loc='upper right')

    # 主循环
    for gen in range(MAX_GEN):

        # --- 计算 ---
        obj_values = zdt1(pop)

        fronts = fast_non_dominated_sort(obj_values)
        rank = np.zeros(POP_SIZE)
        full_distance = np.zeros(POP_SIZE)  # 用于存储所有个体的距离

        for r, front in enumerate(fronts):
            for i in front:
                rank[i] = r
            dists = crowding_distance_assignment(obj_values, front)
            # 映射回全局索引
            for i, idx in enumerate(front):
                full_distance[idx] = dists[i]

        # --- 绘图 (Trace Effect) ---

        # 1. 绘制当前种群作为"历史痕迹" (Trace)
        # 关键优化：
        # - c='lightblue': 浅蓝色
        # - alpha=0.5: 半透明
        # - zorder=1: 放在最底层，不会遮挡红色前沿
        # - label='_nolegend_': 下划线开头告诉 matplotlib 不要在图例中显示它
        ax.scatter(obj_values[:, 0], obj_values[:, 1],
                   c='lightblue', s=10, alpha=0.6, zorder=1, label='_nolegend_')

        # 2. 更新红色前沿 (只更新数据位置，不重画对象)
        current_pareto = obj_values[fronts[0]]
        sc_best_front.set_offsets(current_pareto)

        # 3. 更新标题
        ax.set_title(f'NSGA-II Trajectory: Gen {gen} / {MAX_GEN}')

        # 4. 刷新画布
        # pause 是为了给 GUI 渲染时间
        plt.pause(0.01)

        # --- 进化 ---
        mating_pool = tournament_selection(pop, rank, full_distance)
        offspring = crossover_mutation(mating_pool, BOUNDS[0], BOUNDS[1])
        offspring_obj = zdt1(offspring)

        merged_pop = np.vstack((pop, offspring))
        merged_obj = np.vstack((obj_values, offspring_obj))

        fronts = fast_non_dominated_sort(merged_obj)
        new_pop_indices = []

        for front in fronts:
            if len(new_pop_indices) + len(front) <= POP_SIZE:
                new_pop_indices.extend(front)
            else:
                dists = crowding_distance_assignment(merged_obj, front)
                # 排序逻辑: (idx, dist)，按 dist 降序
                front_with_dist = sorted(zip(front, dists), key=lambda x: x[1], reverse=True)
                n_needed = POP_SIZE - len(new_pop_indices)
                new_pop_indices.extend([x[0] for x in front_with_dist[:n_needed]])
                break

        pop = merged_pop[new_pop_indices]

    print("优化完成。")
    plt.ioff()
    plt.show()


if __name__ == "__main__":
    main()