深入解析遗传算法(GA)：从生物进化论原则到MATLAB高阶实现

引言：自然界的算法智慧

在计算科学的广袤疆域中，人类常常向最古老的工程师——自然——寻求灵感。经过数十亿年的试错与迭代，生物进化演绎出了一套近乎完美的生存优化机制。

遗传算法（Genetic Algorithm, GA）正是约翰·霍兰德（John Holland）教授于20世纪70年代受达尔文生物进化论启发而创立的一类随机搜索算法。它并非仅仅是一种“模拟”，而在数学上模拟了自然界中**“物竞天择，适者生存”**的随机优化过程。

本文将摒弃浅尝辄止的科普，从第一性原理（First Principles）出发，探讨GA为何有效、其背后的数学动力学，并最终落实到鲁棒的MATLAB代码实现。

---

第一部分：理论基石与数学本质

1.1 优化的本质与搜索空间

在物理学和经济学中，我们经常面临寻找系统“能量最低点”或“效用最高点”的问题。这在数学上等价于在一个复杂的多维曲面（Landscape）上寻找全局极值。

传统的基于梯度的算法（如牛顿法、梯度下降）在凸函数（Convex Function）上表现优异，但在面对非线性、非凸、多模态（Multimodal）的复杂函数时，往往陷入局部最优（Local Optima）的陷阱。

遗传算法作为一种启发式全局搜索算法（Global Heuristic Search），其核心优势在于：

1. 并行性：它不是单点搜索，而是维护一个种群（Population），相当于多点同时探索。
2. 随机性与确定性的结合：通过概率性的变异防止早熟收敛，通过选择机制保留优良信息。

1.2 核心隐喻：从生物学到计算机科学

GA的运作依赖于以下映射关系：

• 个体（Individual） $\longleftrightarrow$ 解（Solution）
• 染色体（Chromosome） $\longleftrightarrow$ 编码（Encoding）
• 适应度（Fitness） $\longleftrightarrow$ 目标函数值（Objective Function Value）
• 环境选择（Selection） $\longleftrightarrow$ 优胜劣汰机制
• 交叉与变异（Crossover & Mutation） $\longleftrightarrow$ 算子（Operators）

1.3 模式定理（Schema Theory）：GA为何有效？

很多人会问：为什么随机的交叉和变异能产生更好的结果？这难道不是单纯的碰运气吗？

要回答这个问题，我们需要理解霍兰德提出的模式定理。这是GA坚实的数学基础。

1.3.1 什么是“模式”？

很多初学者在接触遗传算法时，会产生一个直觉上的疑问：

“把两个好的解切开再拼在一起，为什么大概率会得到一个更好的解？这难道不是像把一只好的猫和一只好的狗切开拼在一起，得到怪物的概率更大吗？”

模式定理（Schema Theory） 就是用来回答这个问题的。它告诉我们，GA 操作的不是整个“猫”或“狗”，而是它们身上那些优秀的**“局部特征”**。

在遗传算法中，染色体通常由 0 和 1 组成。为了研究哪些特征被保留了下来，霍兰德引入了一个通配符 *。

• * 代表：这里可以是 0，也可以是 1。

举个例子：
假设我们有一个寻找“最高分”的问题，解的长度是 7 位。

• 我们发现，凡是开头是 1，结尾是 1 的解，分数都很高。
• 中间几位是什么无所谓。
• 那么，这就形成了一个模式：$H = 1 * * * * * 1$。

这个模式就像一个模板，涵盖了所有符合这个特征的解（如 1000001, 1111111 等）。

1.3.2 模式的两个关键属性

要理解为什么有的模式能活下来，有的会死掉，必须看两个指标：

A. 阶数 (Order) - $o(H)$

• 定义：模式中确定位置（非 * 号）的个数。
• 例子：
  • * * 1 * * * * $\rightarrow$ 阶数为 1（很简单，容易凑齐）。
  • 1 0 1 1 * 0 1 $\rightarrow$ 阶数为 6（很复杂，很难凑齐）。
• 直觉：越简单的东西，越容易在变异中存活。

B. 定义距 (Defining Length) - $\delta(H)$

• 定义：模式中，第一个确定位置和最后一个确定位置之间的距离。
• 例子：
  • 模式 A：1 * * * * * 1 $\rightarrow$ 距离是 $7-1=6$（跨度极大）。
  • 模式 B：* * 1 1 * * * $\rightarrow$ 距离是 $4-3=1$（非常紧凑）。
• 直觉（关键点）：
  想象我们要进行单点交叉（在随机位置切一刀，交换左右两边）。
  • 模式 A (跨度大)：因为两头都有固定值，中间无论在哪切一刀，这个模式都会被切断，父亲的头和母亲的尾巴分家了，模式就被破坏了。
  • 模式 B (紧凑)：只有刀正好切在第3和第4位中间时，模式才会被破坏。这种概率很小。

1.3.3 模式定理的核心逻辑

基于上述属性，霍兰德得出了结论。我们可以用一句通俗的话来概括复杂的数学公式：

“在进化过程中，那些【短小的】、【低阶的】、且【适应度高】的模式，其子代数量会呈指数级增长。”

这被称为积木块假设的数学支撑。这个结论包含三个条件：

1. 短小（定义距短）：不容易被交叉切断（抗干扰）。
2. 低阶（固定位少）：不容易被变异破坏（抗变异）。
3. 适应度高：在轮盘赌或锦标赛中容易被选中（高繁殖率）。

满足这三个条件的模式，被称为 “积木块” (Building Blocks) 。

1.3.4 积木块假设：GA 到底在干什么？

现在我们终于可以回答最开始的问题了。遗传算法的本质，不是在随机碰运气凑整个解，而是在拼积木。

1. 第一阶段：种群中随机出现了一些稍微好一点的短小片段（比如 * * 1 1 * * *），因为它们适应度高且不易破坏，所以在种群中迅速扩散。
2. 第二阶段：种群中又出现了另一个好的短片段（比如 1 0 * * * * *）。
3. 第三阶段（交叉的作用）：
   • 父代 1 携带积木块 A：* * 1 1 * * *
   • 父代 2 携带积木块 B：1 0 * * * * *
   • 交叉！
   • 子代完美结合了两者：1 0 1 1 * * *

1.3.5 数学表达

霍兰德通过数学推导证明：在进化过程中，那些低阶、定义距短且平均适应度高于种群平均水平的模式，其样本数将呈指数级增长。

公式如下：
$$
m(H, t+1) \ge m(H,t) \cdot \frac{f(H)}{\bar{f}} \left[ 1 - p_c \frac{\delta(H)}{l-1} - o(H)p_m \right]
$$

其中：

• $m(H, t)$：第 $t$ 代中包含模式 $H$ 的个体数量。
• $f(H) / \bar{f}$：该模式的相对适应度优势。如果大于1，说明该模式比平均水平好，数量会增长。
• 后面括号内的项：表示该模式在交叉和变异中不被破坏的概率。定义距 $\delta(H)$ 越短（即积木块越紧凑），越不容易被切断。

总结：
GA 的搜索过程，就是通过选择算子筛选出优秀的“积木块”，然后通过交叉算子把这些“积木块”拼接在一起，最终组合成全局最优解。

---

第二部分：算法架构深度剖析

遗传算法并非单一的算法，而是一个模块化的框架（Framework）。通过组装不同的编码方式和算子，它可以适应从函数优化到路径规划的各种问题。

一个成熟的 GA 系统，其生命周期包含以下五个核心组件：

2.1 编码策略（Encoding）：基因型与表现型

编码是 GA 设计的第一步，它决定了算法如何在计算机内存中表示现实世界的解。这涉及两个概念的映射：

• 表现型（Phenotype）：问题空间中的实际解（例如：某产品的物理尺寸 $x=5.2$）。
• 基因型（Genotype）：遗传空间中的编码串（例如：二进制串 0101...）。

A. 二进制编码 (Binary Encoding)

这是霍兰德最初提出的经典方法。

• 原理：将参数离散化并映射为 0/1 字符串。
• 优点：符合模式定理的假设，易于理论分析；适用于背包问题（Knapsack Problem）等组合优化。
• 缺点（致命）：
  1. 精度限制：受限于编码长度，无法精确表示连续实数。
  2. 海明悬崖 (Hamming Cliff)：例如数字 7 (0111) 和 8 (1000) 在数值上相邻，但二进制每一位都不同。变异算子很难通过微小的改变跨越这个鸿沟。

B. 实数编码 (Real-value Encoding)

现代工程优化的主流选择。

• 原理：基因就是一个浮点数向量 $[x_1, x_2, …, x_n]$。
• 优点：
  1. 高精度：直接利用计算机浮点数精度。
  2. 直观：无需编解码，且可以使用梯度相关的启发式信息。
  3. 拓扑一致性：解空间中距离近的点，在编码空间中也近。

2.2 适应度函数设计 (Fitness Engineering)

适应度 $F(x)$ 是环境对个体的评价，是进化的唯一动力。设计不当会导致算法失效。

A. 目标函数映射

适应度必须非负。对于最小化问题 $min \ f(x)$，常用的转换映射为：
$$
F(x) = \frac{1}{f(x) + \epsilon} \quad (\epsilon \text{为防零小量})
$$

B. 适应度定标 (Scaling)

原始适应度往往存在问题：

• 进化初期：可能存在少数“超级个体”，其适应度远超平均值。若直接使用，它们会迅速霸占种群，导致早熟收敛。
• 进化后期：所有个体适应度都很高且接近，选择压力极小，进化停滞。

解决方案是使用线性定标或排序定标，动态调整适应度差异，维持恒定的选择压力。

C. 约束处理 (Constraint Handling)

现实问题往往带有约束（如 $g(x) \le 0$）。GA 最常用的方法是罚函数法（Penalty Function）：
$$
F’(x) = F(x) - P(x)
$$
如果个体违反约束，就扣除其适应度。“死刑”（直接剔除）往往不可取，因为不可行解可能携带优良的基因片段。

2.3 选择算子 (Selection)：进化的压力阀

选择操作决定了“谁有资格当父母”。它体现了进化的方向性。

策略	原理描述	优点	缺点
轮盘赌 (Roulette Wheel)	选中概率与适应度成正比 $P_i \propto F_i$	理论经典，体现概率性	对适应度数值敏感，易受超级个体影响导致早熟
随机遍历采样 (SUS)	类似轮盘赌，但使用等距离的多个指针一次性旋转	保持了统计特征，且减少了随机噪声	实现略复杂，依然对定标敏感
锦标赛选择 (Tournament)	随机抽取 $k$ 个个体比武，胜者入选	工业界首选。无需适应度归一化，支持负值，可并行化	需调整 $k$ 值：$k$ 越大，选择压力越大，收敛越快但易早熟

2.4 交叉算子 (Crossover)：信息的重组

交叉是 GA 区别于其他元启发式算法（如模拟退火）的核心特征。它是**探索（Exploration）**的主要手段。

A. 离散交叉（针对二进制）

• 单点交叉：随机选一个切点交换。
• 均匀交叉：每一位都以 0.5 的概率交换。均匀交叉破坏长距离模式，但重组能力更强。

B. 实数交叉（针对连续优化）

• 算术交叉 (Arithmetic Crossover)：
  两个父代向量 $x_1, x_2$ 产生线性组合：
  $$
  y_1 = \alpha x_1 + (1-\alpha) x_2
  $$
  这允许子代探索父代连线上的中间区域。
• 模拟二进制交叉 (SBX)：
  这是 NSGA-II 等高级算法的标准配置。它在实数域上模拟了二进制单点交叉的分布特性，具有优秀的搜索能力。

2.5 变异算子 (Mutation)：多样性的源泉

变异是防止算法陷入局部最优 (Local Optima) 的最后一道防线。它通过随机改变基因值，为种群引入新的遗传物质。

A. 常见变异方式

• 位翻转 (Bit-flip)：针对二进制编码。随机选择一位，将 0 变为 1，或 1 变为 0。
• 高斯变异 (Gaussian Mutation)：针对实数编码。在原有基因值 $x$ 上叠加一个服从正态分布的随机扰动：
  $$x’ = x + N(0, \sigma^2)$$
  关键点：这里的标准差 $\sigma$ 决定了扰动的幅度。$\sigma$ 越大，基因变化的范围越广；$\sigma$ 越小，基因变化越微小。因此，我们可以将 $\sigma$ 理解为搜索的**“步长” (Step Size)**。

B. 高级技巧：非均匀变异（自适应步长）

为了平衡全局探索与局部开发，我们不应使用固定的 $\sigma$，而应使其随时间动态调整：

1. 进化初期：设定较大的 $\sigma$（大步长）。这允许个体在解空间中进行长距离跳跃，快速扫描全局，避免过早陷入局部陷阱。
2. 进化后期：随着代数增加，逐渐减小 $\sigma$（小步长）。这使得算法在已发现的优质区域附近进行精细的微调，以逼近最高精度的最优解。

这正是模拟退火 (Simulated Annealing) 思想在遗传算法中的体现。本文提供的代码即采用了这种 $StepSize \propto (1 - t/T_{max})^2$ 的衰减策略。

---

第三部分：全局探索与局部开发（Exploration vs. Exploitation）

这是所有启发式搜索算法（Heuristic Search）必须面对的核心博弈，常被称为**“探索-开发困境”**。

遗传算法的性能，完全取决于如何在这两者之间维持微妙的动态平衡。

3.1 概念定义与对立统一

• 局部开发（Exploitation / Intensification）

  • 定义：利用目前种群中已知的优良信息，在优质个体附近进行精细搜索，试图找到该区域的局部极值。
  • 主导算子：选择（Selection）和交叉（Crossover）。选择算子通过剔除劣质解，将计算资源集中在优质解上；交叉算子则通过组合现有的“基因块”，在解的邻域内进行重组。
  • 风险：若开发过强，种群会迅速丧失多样性，所有个体趋同。一旦陷入局部最优（Local Optima），算法将无法逃离，导致 “早熟收敛”（Premature Convergence） 。

• 全局探索（Exploration / Diversification）

  • 定义：打破当前的搜索路径，跳跃到搜索空间中未被访问的区域，寻找潜在的全局最优解。
  • 主导算子：变异（Mutation）。变异为种群引入了全新的遗传物质，是产生新信息的源头。
  • 风险：若探索过强，算法将难以稳定在最优解附近，导致搜索过程退化为效率低下的 “随机漫步”（Random Walk），收敛速度极慢。

3.2 动态平衡的艺术

一个优秀的遗传算法，其搜索过程通常呈现**“先宽后窄”**的特征：

1. 初期：侧重全局探索。通过较大的变异概率或多样化的初始种群，快速扫描整个解空间，避免在一开始就陷入局部陷阱。
2. 后期：侧重局部开发。随着代数增加，算法应逐渐收敛于几个有希望的区域，并进行精细化搜索以逼近精确解。

3.3 精英保留策略（Elitism Strategy）：收敛的数学保障

在强烈的随机变异（探索）和交叉重组中，一个很现实的风险是：当前一代中找到的最优解（Best-so-far），可能会在下一代因为变异或交叉而被破坏。

为了解决这个问题，我们引入精英策略。

• 机制：在生成下一代之前，强制将当前种群中适应度最高的 $N_{elite}$ 个个体，不经任何变异直接复制到下一代种群中。
• 数学意义：
  从马尔可夫链（Markov Chain）的角度分析，标准的遗传算法（无精英策略）通常不具备“全局收敛性”。Rudolph (1994) 从理论上证明了：只有引入精英策略，典型的遗传算法才能保证以概率 1 收敛于全局最优解。
  它起到了一种“棘轮效应”（Ratchet Effect）：保证了算法的历史最佳适应度是一个单调不减的序列。

---

第四部分：MATLAB 实现

下面提供一个模块化、鲁棒的遗传算法实现。我们将求解一个经典的非线性多模态函数：

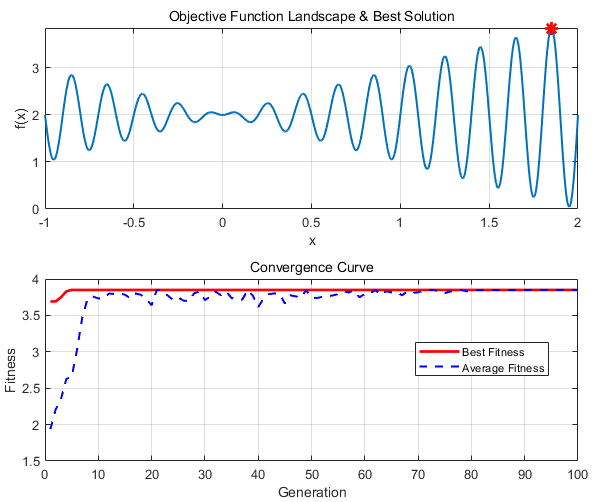
$$f(x) = x \cdot \sin(10\pi x) + 2.0$$
在区间 $[-1, 2]$ 上寻找最大值。

此代码采用实数编码和精英策略，并包含了自适应变异步长的设计。

4.1 主程序 (Main Script)

% =========================================================================
% Genetic Algorithm (GA) - 修正版
% =========================================================================

clear; clc; close all;

%% 1. 参数初始化与目标函数定义 (Configuration)
GA_Params.PopSize     = 100;        % 种群规模
GA_Params.MaxGen      = 100;        % 最大迭代次数
GA_Params.Pc          = 0.8;        % 交叉概率
GA_Params.Pm          = 0.05;       % 变异概率
GA_Params.ElitismRate = 0.05;       % 精英保留比例
GA_Params.VarRange    = [-1, 2];    % 搜索空间范围 [min, max]

% --- [关键修改] 使用匿名函数定义目标函数 ---
% 这样可以直接在脚本中调用，避免命名冲突
ObjFun = @(x) x .* sin(10 * pi * x) + 2.0;

% 衍生参数
nElite = round(GA_Params.PopSize * GA_Params.ElitismRate);

%% 2. 初始化 (Initialization)
pop = GA_Params.VarRange(1) + ...
      (GA_Params.VarRange(2) - GA_Params.VarRange(1)) * rand(GA_Params.PopSize, 1);

bestFitnessHist = zeros(GA_Params.MaxGen, 1);
avgFitnessHist  = zeros(GA_Params.MaxGen, 1);

%% 3. 进化主循环 (Main Loop)
for gen = 1:GA_Params.MaxGen
    
    % --- [关键修改] 调用匿名函数句柄 ---
    fitness = ObjFun(pop); 
    
    % 记录统计数据
    [maxVal, maxIdx] = max(fitness);
    bestFitnessHist(gen) = maxVal;
    avgFitnessHist(gen) = mean(fitness);
    bestIndiv = pop(maxIdx);
    
    % 显示进度
    fprintf('Gen: %3d | Best Fitness: %.5f | Best Var: %.5f\n', ...
            gen, maxVal, bestIndiv);
            
    % --- 精英策略 ---
    [~, sortedIdx] = sort(fitness, 'descend');
    elitePop = pop(sortedIdx(1:nElite));
    
    % --- 选择 (锦标赛) ---
    matingPool = TournamentSelection(pop, fitness, GA_Params.PopSize - nElite);
    
    % --- 交叉 (算术交叉) ---
    offspring = Crossover(matingPool, GA_Params.Pc, GA_Params.VarRange);
    
    % --- 变异 (自适应高斯变异) ---
    offspring = Mutation(offspring, GA_Params.Pm, GA_Params.VarRange, gen, GA_Params.MaxGen);
    
    % --- 生成下一代 ---
    pop = [elitePop; offspring]; 
end

%% 4. 可视化 (Visualization)
figure('Color', 'w');
subplot(2,1,1);
fplot(ObjFun, GA_Params.VarRange, 'LineWidth', 1.5); % 使用定义的句柄
hold on;
plot(bestIndiv, maxVal, 'r*', 'MarkerSize', 10, 'LineWidth', 2);
title('Objective Function Landscape & Best Solution');
xlabel('x'); ylabel('f(x)');
grid on;

subplot(2,1,2);
plot(bestFitnessHist, 'r-', 'LineWidth', 2);
hold on;
plot(avgFitnessHist, 'b--', 'LineWidth', 1.5);
title('Convergence Curve');
xlabel('Generation'); ylabel('Fitness');
legend('Best Fitness', 'Average Fitness');
grid on;

%% --- 辅助函数 (保持不变，必须放在文件底部) ---

function selected = TournamentSelection(pop, fitness, nNeeded)
    popSize = length(pop);
    selected = zeros(nNeeded, 1);
    tournamentSize = 3; 
    for i = 1:nNeeded
        candidatesIdx = randi(popSize, [tournamentSize, 1]);
        candidateFitness = fitness(candidatesIdx);
        [~, bestIdxLocal] = max(candidateFitness);
        selected(i) = pop(candidatesIdx(bestIdxLocal));
    end
end

function offspring = Crossover(parents, Pc, range)
    numParents = length(parents);
    offspring = parents; 
    for i = 1:2:numParents-1
        if rand < Pc
            alpha = rand;
            p1 = parents(i);
            p2 = parents(i+1);
            c1 = alpha * p1 + (1-alpha) * p2;
            c2 = (1-alpha) * p1 + alpha * p2;
            offspring(i)   = max(min(c1, range(2)), range(1));
            offspring(i+1) = max(min(c2, range(2)), range(1));
        end
    end
end

function mutated = Mutation(pop, Pm, range, currentGen, maxGen)
    mutated = pop;
    numIndiv = length(pop);
    scale = range(2) - range(1);
    stepSize = 0.1 * scale * (1 - currentGen/maxGen)^2;
    for i = 1:numIndiv
        if rand < Pm
            delta = randn * stepSize;
            newVal = pop(i) + delta;
            mutated(i) = max(min(newVal, range(2)), range(1));
        end
    end
end

运行结果如下图：

第五部分：Python (NumPy) 工程实现

在生产环境、Web后端或深度学习集成中，Python 是不二之选。我们将使用 numpy 进行向量化操作以提升性能。

5.1 Python 代码特性

• 向量化 (Vectorization)：利用 NumPy 数组运算替代显式循环，极大提高执行效率。
• 面向对象 vs 函数式：为了与 MATLAB 版本保持逻辑对应，本示例采用函数式编程风格，清晰展示每一步的算子操作。

5.2 完整 Python 代码

import numpy as np
import matplotlib.pyplot as plt

# =========================================================================
# Genetic Algorithm (GA) - Python NumPy Implementation
# Author: Professional Blog Creator
# =========================================================================

# --- 1. 配置参数 ---
POP_SIZE = 100          # 种群规模
MAX_GEN = 100           # 最大迭代次数
P_CROSSOVER = 0.8       # 交叉概率
P_MUTATION = 0.05       # 变异概率
ELITISM_RATE = 0.05     # 精英保留比例
VAR_RANGE = [-1, 2]     # 搜索范围 [min, max]

# 计算精英数量
N_ELITE = int(POP_SIZE * ELITISM_RATE)

# --- 2. 核心函数定义 ---

def objective_function(x):
    """目标函数: f(x) = x * sin(10*pi*x) + 2.0"""
    return x * np.sin(10 * np.pi * x) + 2.0

def tournament_selection(pop, fitness, num_needed, tournament_size=3):
    """锦标赛选择"""
    selected = np.zeros(num_needed)
    for i in range(num_needed):
        # 随机抽取候选者索引
        candidates_idx = np.random.randint(0, len(pop), size=tournament_size)
        # 找到候选者中适应度最高的索引
        best_candidate_idx = candidates_idx[np.argmax(fitness[candidates_idx])]
        selected[i] = pop[best_candidate_idx]
    return selected

def crossover(parents, pc, var_range):
    """算术交叉"""
    offspring = parents.copy()
    num_parents = len(parents)
    
    # 步长为2，处理每一对父母
    for i in range(0, num_parents - 1, 2):
        if np.random.rand() < pc:
            alpha = np.random.rand()
            p1 = parents[i]
            p2 = parents[i+1]
            
            # 线性插值混合
            c1 = alpha * p1 + (1 - alpha) * p2
            c2 = (1 - alpha) * p1 + alpha * p2
            
            # 边界截断
            offspring[i]   = np.clip(c1, var_range[0], var_range[1])
            offspring[i+1] = np.clip(c2, var_range[0], var_range[1])
            
    return offspring

def mutation(pop, pm, var_range, current_gen, max_gen):
    """自适应高斯变异"""
    mutated = pop.copy()
    scale = var_range[1] - var_range[0]
    
    # 自适应步长：随代数增加而减小 (Explore -> Exploit)
    step_size = 0.1 * scale * (1 - current_gen / max_gen)**2
    
    for i in range(len(pop)):
        if np.random.rand() < pm:
            # 施加高斯噪声
            delta = np.random.randn() * step_size
            new_val = pop[i] + delta
            mutated[i] = np.clip(new_val, var_range[0], var_range[1])
            
    return mutated

# --- 3. 主程序 ---

def main():
    # 初始化种群
    pop = np.random.uniform(VAR_RANGE[0], VAR_RANGE[1], POP_SIZE)
    
    best_fitness_history = []
    avg_fitness_history = []
    best_solution = None
    best_val = -np.inf

    print(f"{'Gen':<5} | {'Best Fitness':<15} | {'Best Var':<15}")
    print("-" * 40)

    for gen in range(MAX_GEN):
        # 1. 评估
        fitness = objective_function(pop)
        
        # 2. 统计
        current_max_idx = np.argmax(fitness)
        current_max_val = fitness[current_max_idx]
        current_best_var = pop[current_max_idx]
        
        best_fitness_history.append(current_max_val)
        avg_fitness_history.append(np.mean(fitness))
        
        # 更新全局最优
        if current_max_val > best_val:
            best_val = current_max_val
            best_solution = current_best_var

        if gen % 10 == 0 or gen == 0:
            print(f"{gen:<5} | {current_max_val:.5f}          | {current_best_var:.5f}")

        # 3. 精英策略 (使用 argsort 获取降序索引)
        sorted_indices = np.argsort(fitness)[::-1] 
        elite_pop = pop[sorted_indices[:N_ELITE]]

        # 4. 选择
        num_offspring_needed = POP_SIZE - N_ELITE
        mating_pool = tournament_selection(pop, fitness, num_offspring_needed)

        # 5. 交叉
        offspring = crossover(mating_pool, P_CROSSOVER, VAR_RANGE)

        # 6. 变异
        offspring = mutation(offspring, P_MUTATION, VAR_RANGE, gen, MAX_GEN)

        # 7. 种群更新 (拼接)
        pop = np.concatenate((elite_pop, offspring))

    print("-" * 40)
    print(f"Final Solution: x = {best_solution:.5f}, f(x) = {best_val:.5f}")

    # --- 4. 可视化 ---
    plt.figure(figsize=(10, 8))
    
    # 绘制函数景观
    plt.subplot(2, 1, 1)
    x = np.linspace(VAR_RANGE[0], VAR_RANGE[1], 500)
    y = objective_function(x)
    plt.plot(x, y, label='Objective Function')
    plt.scatter(best_solution, best_val, color='red', s=100, zorder=5, label='Best Found')
    plt.title('Objective Landscape')
    plt.grid(True)
    plt.legend()

    # 绘制收敛曲线
    plt.subplot(2, 1, 2)
    plt.plot(best_fitness_history, 'r-', label='Best Fitness')
    plt.plot(avg_fitness_history, 'b--', label='Avg Fitness')
    plt.title('Convergence Curve')
    plt.xlabel('Generation')
    plt.ylabel('Fitness')
    plt.grid(True)
    plt.legend()
    
    plt.tight_layout()
    plt.show()

if __name__ == "__main__":
    main()

代码解析：关键设计决策

1. 锦标赛选择：无需对适应度归一化，计算速度快且利于并行化。
2. 算术交叉：实数编码特有的交叉方式，比单纯交换基因更能挖掘两个解中间的潜在优质区域。
3. 非均匀变异 (Non-uniform Mutation)：请注意 stepSize 的计算。随着迭代进行，变异的扰动幅度逐渐减小。这模仿了模拟退火的思想：初期大步探索（Global Exploration），后期精细微调（Local Exploitation）。
4. 精英策略：代码中通过排序强制保留了 Top 5% 的个体，这是防止解退化的安全网。

---

第六部分：前沿拓展与现代演进

标准遗传算法（SGA）只是进化计算的起点。面对更复杂的现实世界挑战（如多目标权衡、超大规模参数），GA 已经衍生出了众多强大的变体：

6.1 多目标优化 (Multi-Objective Optimization)

现实工程问题往往充满矛盾。例如在设计发动机时，我们既希望 “动力最大化”，又希望 “油耗最小化”。这两个目标通常是冲突的。

• 解决方案：NSGA-II / NSGA-III (Non-dominated Sorting GA)。
• 核心思想：不再寻找单一的最优解，而是寻找一组帕累托最优解集 (Pareto Front)。在这个集合中，任何一个解的性能提升都必然导致另一个目标的下降，决策者需根据实际需求从中折衷。

6.2 文化基因算法 (Memetic Algorithm)

GA 擅长全局搜索（找大概位置），但往往在局部精细搜索（找精确小数点）上效率不如梯度法。

• 解决方案：将 GA 与局部搜索算法（如爬山法、牛顿法或模拟退火）结合。
• 机制：“全局统筹，局部精修”。GA 负责将种群带到极值附近，然后对每个个体运行几步局部搜索，使其达到自身潜能的极限。这种“先天遗传 + 后天学习”的模式大大提高了收敛速度。

6.3 岛屿模型与并行计算 (Island Model)

对于计算昂贵的适应度函数（如流体动力学 CFD 仿真），单线程 GA 难以胜任。

• 解决方案：将大种群分割为若干个子种群，分布在不同的 CPU 核心（“岛屿”）上独立进化。
• 机制：每隔若干代，相邻岛屿之间会发生 “迁徙 (Migration)”，交换少量优秀个体。这不仅利用了并行计算资源，还能通过地理隔离有效维持全局多样性，防止早熟。

结语

遗传算法是计算智能皇冠上的明珠之一。它打破了我们对算法的刻板印象：完美并非只能通过精密的数学推导设计出来，也可以在混沌与随机中通过“试错”进化出来。

从基础的模式定理到复杂的协同进化，GA 为我们提供了一种处理非线性、非凸、黑盒优化问题的通用框架。

无论是使用 MATLAB 进行快速的原型验证，还是利用 Python 在生产环境中构建大规模优化系统，掌握 GA 的核心思想，都将使你在面对复杂系统设计时，拥有一把刺破迷雾的利剑。