从数据到智能：机器学习核心方法的数学原理与全景解构

引言：逼近真理的函数

如果我们还原到最本质的层面，机器学习（Machine Learning）的目标究竟是什么？

在物理学中，我们试图通过牛顿定律或麦克斯韦方程组来描述宇宙的运行机制，这是一种演绎（Deductive）的过程——先有公式，再解释现象。而机器学习，本质上是一个归纳（Inductive）的过程。我们在高维空间中观察数据点的分布，试图寻找一个函数 $f(x)$，使得它能够最大程度地逼近真实世界的规律 $y$。

用数学语言描述，假设真实世界存在一个未知的映射关系 $Y = F(X) + \epsilon$，其中 $\epsilon$ 是不可约减的随机噪声。机器学习的任务就是在假设空间（Hypothesis Space）$\mathcal{H}$ 中寻找一个最优函数 $f \in \mathcal{H}$，使得某种定义的损失函数（Loss Function）$L(Y, f(X))$ 的期望风险最小化：

$$
f^* = \arg\min_{f \in \mathcal{H}} \mathbb{E}_{(X,Y) \sim \mathcal{D}} [L(Y, f(X))]
$$

本文将剥离繁杂的代码库调用，从数学和逻辑的底层出发，详细剖析支撑现代人工智能大厦的几根支柱：监督学习、无监督学习以及深度学习，并探讨它们如何在统计学、几何学和微积分的交汇点上产生智能。

---

第一部分：监督学习——在教师指引下的优化

监督学习（Supervised Learning）是目前工业界应用最成熟的范式。其核心在于“标签”。我们拥有一组带有标准答案的数据 ${(x_1, y_1), …, (x_n, y_n)}$，算法的目标是学习输入 $x$ 到输出 $y$ 的映射。

1. 线性回归：统计学的基石

线性回归（Linear Regression）往往被轻视，但它是理解模型优化的起点。

第一性原理视角

为什么我们常用“最小二乘法”（Ordinary Least Squares, OLS）？为什么不是最小绝对值误差？

从概率论的角度看，如果假设数据中的噪声 $\epsilon$ 服从正态分布 $\epsilon \sim \mathcal{N}(0, \sigma^2)$，那么根据最大似然估计（Maximum Likelihood Estimation, MLE），最大化观测数据的概率等价于最小化预测误差的平方和。

模型假设：
$$ h_\theta(x) = \theta^T x + b $$

损失函数（均方误差）：
$$ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 $$

正规方程与梯度下降

求解这个极值问题有两种途径：

1. 解析解（Closed-form）：通过矩阵微积分直接令导数为0，得到正规方程 $\theta = (X^T X)^{-1} X^T y$。这展示了线性代数中投影矩阵的优美几何性质——预测向量 $\hat{y}$ 是观测向量 $y$ 在列空间上的正交投影。
2. 数值优化：当数据量极大导致矩阵求逆极其昂贵时，我们使用梯度下降（Gradient Descent）。这如同物理学中的势能最小化，小球沿着曲面最陡峭的方向滚落谷底。

2. 支持向量机（SVM）：几何间隔的最大化

如果说线性回归是统计学的产物，那么支持向量机（Support Vector Machine）则是几何学的胜利。

核心思想：最大间隔

对于分类问题，能将数据分开的超平面有无数个。SVM 追求的是鲁棒性（Robustness）。它寻找一个超平面，使得距离该超平面最近的样本点（即支持向量）的距离最大化。

数学上，这被转化为一个凸优化问题：

$$
\begin{aligned}
& \min_{w, b} \frac{1}{2} ||w||^2 \
& \text{s.t. } y^{(i)}(w^T x^{(i)} + b) \geq 1, \quad \forall i
\end{aligned}
$$

核技巧（Kernel Trick）的升维智慧

SVM 的真正威力在于处理非线性可分数据。通过拉格朗日对偶性（Lagrange Duality），我们将原始问题转化为对偶问题，发现计算只涉及样本间的内积 $\langle x_i, x_j \rangle$。

通过核函数 $K(x_i, x_j) = \langle \phi(x_i), \phi(x_j) \rangle$，我们将低维不可分的数据映射到高维（甚至是无限维）的希尔伯特空间中。这体现了一个深刻的数学哲学：在低维空间纠缠不清的复杂关系，往往在高维空间看只是简单的线性关系。

3. 决策树与集成方法：信息熵的衰减

决策树（Decision Tree）不依赖复杂的代数运算，而是模仿人类的逻辑判断规则。

信息论基础

如何选择分裂特征？这是决策树的核心。这里引入了香农（Shannon）的信息论概念——熵（Entropy）。熵度量了系统的不确定性：

$$ H(X) = - \sum_{i=1}^{n} p(x_i) \log p(x_i) $$

算法（如ID3, C4.5, CART）通过最大化**信息增益（Information Gain）或最小化基尼不纯度（Gini Impurity）**来贪婪地分割数据空间。这本质上是一个不断消除系统不确定性的过程。

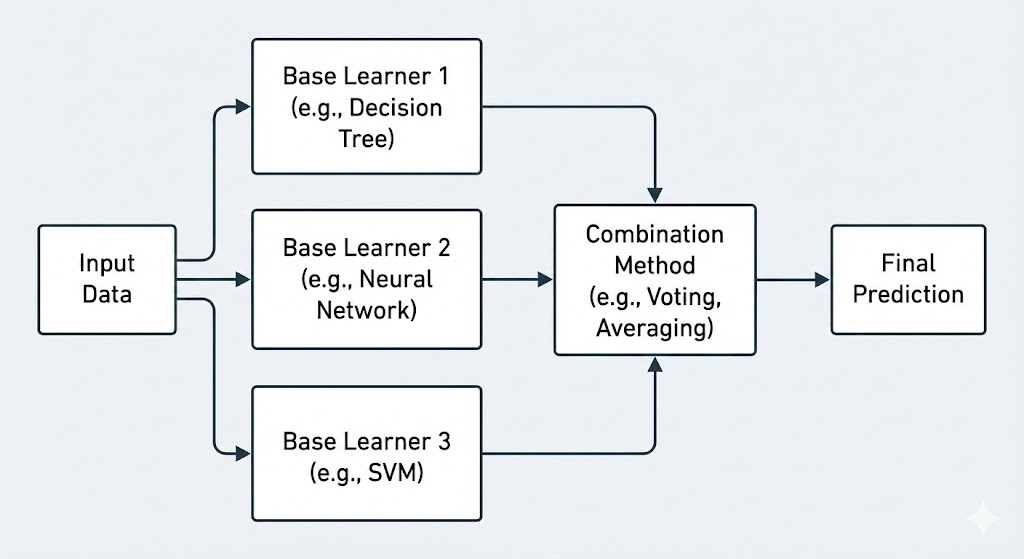
集成学习：群体的智慧

单个决策树容易过拟合（High Variance）。集成学习（Ensemble Learning）利用了统计学中的大数定律。

• Bagging (Random Forest)：通过自助采样法（Bootstrap）构建多个相互独立的强分类器并取平均。这在数学上有效地降低了模型的方差（Variance）。
• Boosting (Gradient Boosting, XGBoost)：串行训练一系列弱分类器，每一个新的分类器都在拟合之前所有分类器的残差（Residual）。这本质上是在函数空间中的梯度下降。

---

第二部分：无监督学习——数据内部结构的探索

在无监督学习（Unsupervised Learning）中，没有“教师”告诉我们答案。我们必须自己发现数据的内在结构。

1. 聚类（K-Means）：期望最大化的特例

K-Means 是最直观的聚类算法，但其背后体现了**EM算法（Expectation-Maximization）**的思想。

• E步（Expectation）：固定中心点，将每个样本分配给最近的中心（更新隐含变量）。
• M步（Maximization）：固定分配结果，重新计算簇的中心以最小化平方误差（参数优化）。

这种交替优化的策略在很多统计模型（如高斯混合模型 GMM）中都有应用。

2. 主成分分析（PCA）：特征值的降维魔法

在高维空间中，数据往往存在“维度灾难”。PCA 是一种线性降维技术，其目标是找到一个新的坐标系，使得数据在新的坐标轴上投影的方差最大。

线性代数解释

从数学上看，PCA 等价于对数据的协方差矩阵 $\Sigma$ 进行特征值分解（Eigendecomposition）：

$$ \Sigma v = \lambda v $$

特征向量 $v$ 指示了主成分的方向，而特征值 $\lambda$ 的大小代表了该方向上数据的方差。通过保留最大的 $k$ 个特征值对应的特征向量，我们在压缩数据的同时，最大程度地保留了信息（方差）。

这不仅是数据压缩，更是一种信号处理：剔除噪声（小特征值方向），保留信号（大特征值方向）。

---

第三部分：深度学习——由简入繁的连接主义

深度学习（Deep Learning）并非一种全新的魔法，而是多层神经网络在算力和大数据加持下的复兴。它模拟了生物神经元的连接方式。

1. 神经网络：通用近似定理

一个单层的神经网络（MLP）理论上可以以任意精度逼近任何连续函数。这就是通用近似定理（Universal Approximation Theorem）。

$$ f(x) = \sigma(W_2 \cdot \sigma(W_1 \cdot x + b_1) + b_2) $$

其中 $\sigma$ 是非线性激活函数（如 ReLU, Sigmoid）。如果没有非线性激活函数，无论多少层神经网络叠加，最终都等价于一个单层线性变换。非线性是智能涌现的关键。

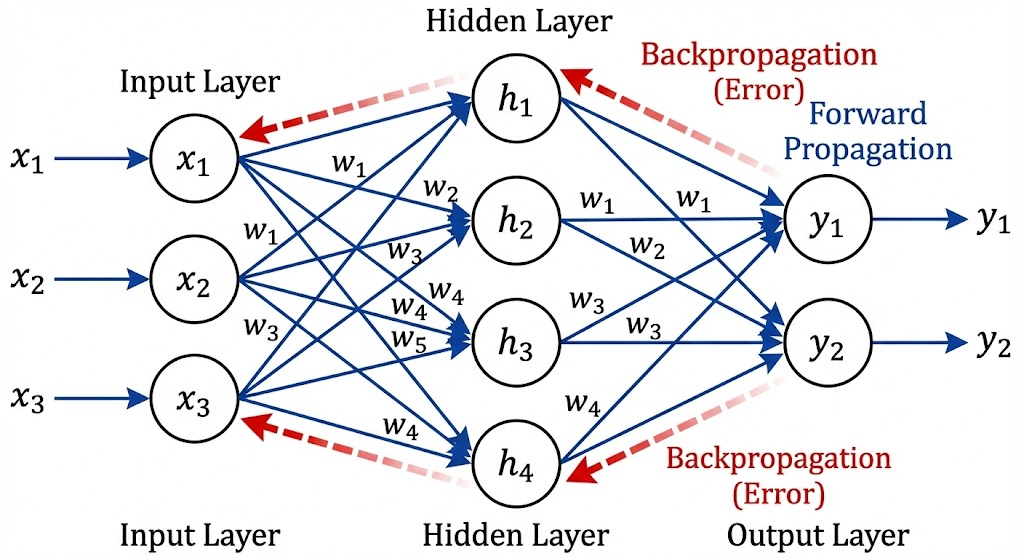
2. 反向传播（Backpropagation）：链式法则的应用

深度学习训练的核心动力是反向传播算法。它本质上是微积分中**链式法则（Chain Rule）**在计算图（Computational Graph）上的高效实现。

对于损失函数 $L$，我们要计算它对网络深层参数 $w$ 的梯度：

$$ \frac{\partial L}{\partial w} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial h} \cdot \frac{\partial h}{\partial w} $$

误差信号通过网络层层回传，指引每个神经元调整权重。

3. 卷积神经网络（CNN）与循环神经网络（RNN）

• CNN 利用了图像的平移不变性（Translation Invariance）和局部相关性。卷积核本质上是一个特征提取器（滤波器）。
• RNN（及其变体 LSTM/Transformer）处理序列数据，引入了时间维度，使得模型具有了“记忆”。

第四部分：模型评估与哲学思考

1. 偏差-方差权衡（Bias-Variance Tradeoff）

这是机器学习中永恒的矛盾。

• 偏差（Bias）：模型对数据假设过于简化（欠拟合）。
• 方差（Variance）：模型对训练数据的随机噪声过于敏感（过拟合）。

优秀的模型不是追求在训练集上 100% 的准确率，而是在偏差和方差之间找到最佳平衡点，从而获得最好的泛化能力（Generalization）。

2. 没有免费午餐定理（No Free Lunch Theorem）

Wolpert 在 1996 年证明：没有任何一种算法能在所有可能的问题上都优于其他算法。

如果我们对数据分布一无所知，那么复杂的神经网络并不比随机猜测好。机器学习的有效性，建立在我们对现实世界数据具有特定结构（如平滑性、局部性、层次性）的先验假设之上。

---

结语：从算法到洞察

机器学习的常用方法，从简单的线性回归到复杂的 Transformer，其本质都是在数学框架下对现实世界的建模。

• 线性代数提供了变换的空间；
• 微积分提供了优化的动力；
• 概率论提供了处理不确定性的语言。

掌握这些方法，不仅仅是学会调用 scikit-learn 或 PyTorch 的 API，更是要理解每一个超参数背后的数学意义，理解数据在流形（Manifold）上的分布。作为工程师和研究者，我们的工作不仅是训练模型，更是透过模型去洞察数据背后隐藏的物理规律和人性逻辑。

未来的机器学习将更加侧重于可解释性（Explainability）和因果推断（Causal Inference），试图不仅仅回答“是什么”，更要回答“为什么”。

# 附：一个简单的梯度下降示例，展示优化的本质
import numpy as np

def gradient_descent(X, y, learning_rate=0.01, epochs=1000):
    m, n = X.shape
    theta = np.zeros(n) # 初始化参数
    
    for _ in range(epochs):
        prediction = np.dot(X, theta)
        error = prediction - y
        # 梯度的计算源于损失函数对theta的偏导数
        gradient = (1/m) * np.dot(X.T, error)
        # 沿梯度反方向更新，模拟"下山"
        theta -= learning_rate * gradient
        
    return theta

这是一场从数据中提炼智慧的漫长旅程，而我们才刚刚启程。