广义斯涅尔定律的完整物理推导
公元 1621 年,威勒布拉德·斯涅尔 (Willebrord Snellius) 发现了著名的折射定律:$n_1 \sin\theta_1 = n_2 \sin\theta_2$。这条定律像一道枷锁,规定了光在穿过两种介质界面时,其折射方向只能由两边的材料属性(折射率)决定。
几个世纪以来,为了控制光,人类不得不打磨各种曲面透镜,通过改变厚度来积累相位。这就是为什么你的相机镜头如此厚重。
直到 2011 年,哈佛大学 Capasso 教授团队提出了广义斯涅尔定律 (Generalized Snell’s Law),指出如果在界面上引入一个相位突变 (Phase Discontinuity),光就可以打破枷锁,实现任意方向的折射。这一发现直接开启了超表面 (Metasurface) 的黄金时代。
但这背后的物理原理究竟是什么?为什么引入相位梯度就能改变光路?
本文将不依赖任何现成结论,从光学的本源——费马原理出发,对这一核心定律进行一次完整的数学推导。
01. 物理原本:费马原理与相位平稳
要推导光怎么走,必须问光遵循什么规则。
费马原理 (Fermat’s Principle) 告诉我们:光在两点之间传播,总是选择光程 (Optical Path Length, OPL) 取极值的路径。
在波动光学中,光程对应着相位 (Phase)。费马原理等价于相位平稳原理 (Principle of Stationary Phase):
对于真实的光路,其总相位积累 $\Psi$ 对路径参数的微分为零。
$$\frac{d\Psi}{dx} = 0$$
这意味着,如果我们考察两条无限接近的真实光路,它们到达同一点时的相位差必须为零(即发生相长干涉)。我们将利用这个微元思想来构建方程。
02. 推导模型构建
让我们建立一个标准的二维物理模型:
- 界面:$y=0$ 平面将空间分为两部分。
- 上方:介质 1,折射率 $n_i$。
- 下方:介质 2,折射率 $n_t$。
- 超表面:在界面上布置了一层亚波长结构,它们在位置 $x$ 处引入了一个额外的相位突变 $\Phi(x)$。
- 入射光:平面波从介质 1 入射,入射角 $\theta_i$。
- 折射光:进入介质 2,折射角 $\theta_t$。
03. 核心推导过程
我们考察两条极度接近的光线路径,它们打在界面上的位置分别为 $A$ 点 ($x$) 和 $B$ 点 ($x+dx$)。
为了满足波前连续性(或者说费马原理),这两条光线在通过界面后,其总相位变化量必须相等。
总相位由三部分组成:
$$\Psi_{total} = \Psi_{in} + \Phi_{interface} + \Psi_{out}$$
我们需要计算这三部分在 $dx$ 距离内的增量。
第一步:入射侧的相位差 ($d\Psi_{in}$)
观察入射光波前(垂直于波矢量的面):
当光线落点从 $x$ 移到 $x+dx$ 时,光线实际上需要多走一段路程才能到达界面。
根据几何关系,这段额外的路程是:
$$dL_{in} = dx \cdot \sin\theta_i$$
对应的相位增量为($k_0 = \frac{2\pi}{\lambda_0}$ 为真空波数):
$$d\Psi_{in} = k_0 n_i \cdot (dx \sin\theta_i)$$
第二步:界面上的相位突变差 ($d\Phi$)
这是经典光学中不存在的项。
由于超表面结构随位置变化,点 $x$ 和点 $x+dx$ 处的微纳结构不同,导致光获得的额外相位也不同。
这个差异就是相位梯度:
$$d\Phi = \frac{d\Phi(x)}{dx} dx$$
第三步:折射侧的相位差 ($d\Psi_{out}$)
观察折射光波前:
当光线从 $x+dx$ 射出时,相比于从 $x$ 射出的光线,它在介质 2 中的行程“缩短”了(或者说,为了保持波前垂直于光线,$x$ 点发出的光已经多走了一段)。
折射侧的几何路程投影为:
$$dL_{out} = dx \cdot \sin\theta_t$$
对应的相位补偿为:
$$d\Psi_{out} = k_0 n_t \cdot (dx \sin\theta_t)$$
第四步:建立平衡方程
根据相位平稳原理,两条路径的总相位必须匹配。
也就是说:入射相位增量 + 界面相位增量 = 折射相位增量
$$k_0 n_i \sin\theta_i \cdot dx + \frac{d\Phi}{dx} dx = k_0 n_t \sin\theta_t \cdot dx$$
04. 广义斯涅尔定律的诞生
消去公因式 $dx$,我们得到:
$$k_0 n_i \sin\theta_i + \frac{d\Phi}{dx} = k_0 n_t \sin\theta_t$$
为了让公式更美观,我们将 $k_0 = \frac{2\pi}{\lambda_0}$ 代入并移项:
$$n_t \sin\theta_t - n_i \sin\theta_i = \frac{\lambda_0}{2\pi} \frac{d\Phi}{dx}$$
这就是震动光学界的广义斯涅尔定律。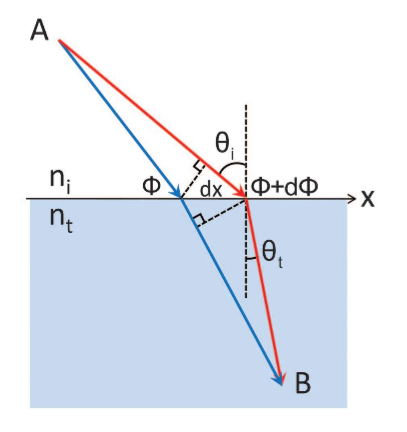
它包含两部分:
- 经典项 ($n_t \sin\theta_t - n_i \sin\theta_i = 0$):如果界面没有相位梯度 ($\frac{d\Phi}{dx}=0$),它就退化为经典的斯涅尔定律。
- 梯度项 ($\frac{d\Phi}{dx}$):这是超表面赋予我们的新自由度。只要设计合适的相位梯度,我们就能任意控制折射角 $\theta_t$。
同理,我们可以推导出广义反射定律:
$$\sin\theta_r - \sin\theta_i = \frac{\lambda_0}{2\pi n_i} \frac{d\Phi}{dx}$$
05. 物理本质:光子动量守恒
这个公式虽然是几何推导出来的,但它背后藏着更深刻的量子力学原理:动量守恒 (Momentum Conservation)。
光子的动量为 $\vec{p} = \hbar \vec{k}$。
在界面切向方向 ($x$ 轴),动量必须守恒。
$$k_{x, out} = k_{x, in} + k_{surface}$$
- $k_{x, in} = k_0 n_i \sin\theta_i$ 是入射光子的切向动量。
- $k_{x, out} = k_0 n_t \sin\theta_t$ 是出射光子的切向动量。
- $\nabla\Phi = \frac{d\Phi}{dx}$ 正是超表面提供给光子的“虚拟动量”。
结论: 超表面本质上是一个动量转换器。它通过精细的结构设计,给路过的光子“踢”了一脚,改变了它的动量大小,从而改变了它的方向。
06. 临界情况:光会消失吗?
观察公式,如果不小心把 $\frac{d\Phi}{dx}$ 设计得太大,使得右边的计算结果大于 $n_t$ 怎么办?
$$\sin\theta_t = \frac{n_i}{n_t}\sin\theta_i + \frac{\lambda_0}{2\pi n_t}\frac{d\Phi}{dx} > 1$$
此时 $\sin\theta_t$ 无实数解。这意味着光无法折射进入介质 2。
光会变成倏逝波 (Evanescent Wave),紧贴着界面传播,能量在垂直方向指数衰减。
这在物理上对应着衍射极限。在设计超透镜 (Metalens) 时,这是一个必须校验的边界条件。
07. 结语
通过这次推导,我们不仅得到了一个公式,更理解了超表面的核心哲学:用空间换相位,用相位换动量。
既然我们知道了 $\frac{d\Phi}{dx}$ 决定了光的方向,那么接下来的问题就是:工程上,我们如何制造出这个 $\Phi(x)$?
这需要我们设计一种微纳结构(人工原子),通过改变它的形状(如圆柱的直径、长方体的角度),来精确控制光穿过它时的相位延迟。