激光模式介绍

在光学工程领域，”激光”二字往往意味着高亮度、高方向性。但如果我们只把激光看作一条几何光线，那理解是表面的。
但如果你调整一下激光器的谐振腔，或者激光经过某些晶体，你会惊讶地发现，光斑变了： 有的变成了“甜甜圈”，有的变成了“田字格”，有的甚至像复杂的万花筒。
这些不同的空间分布形态，就是激光的横模 (Transverse Modes)。今天我们来拆解一下这些模式背后的物理与数学之美。

第一章：高斯光束数学起源——傍轴波动方程

所有的光，首先必须满足麦克斯韦方程组。在均匀、各向同性的介质中，电场 $\vec{E}$ 满足矢量波动方程：
$$\nabla^2 \vec{E} - \mu \epsilon \frac{\partial^2 \vec{E}}{\partial t^2} = 0$$

1.1 亥姆霍兹方程

对于单色光（频率 $\omega$），我们可以分离时间项 $\vec{E}(\vec{r}, t) = E(\vec{r}) e^{-i\omega t}$，得到标量亥姆霍兹方程 (Helmholtz Equation)：
$$\nabla^2 E + k^2 E = 0$$
其中 $k = \omega \sqrt{\mu \epsilon} = 2\pi / \lambda$ 是波数。

1.2 缓慢包络近似 (SVEA)

激光通常沿特定方向（设为 z 轴）传播，且发散角很小。我们可以假设解的形式为：
$$E(x, y, z) = u(x, y, z) e^{-ikz}$$
其中 $e^{-ikz}$ 是快速振荡的平面波因子，而 $u(x, y, z)$ 是缓慢变化的复振幅包络。

将此代入亥姆霍兹方程，我们得到：
$$\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} - 2ik \frac{\partial u}{\partial z} = 0$$

傍轴近似 (Paraxial Approximation) 的核心在于：包络 $u$ 随 $z$ 的变化非常慢，远小于波长的尺度。因此，我们可以忽略二阶导数项 $\left| \frac{\partial^2 u}{\partial z^2} \right| \ll \left| 2k \frac{\partial u}{\partial z} \right|$。

最终，我们得到了著名的傍轴波动方程：
$$\nabla_T^2 u - 2ik \frac{\partial u}{\partial z} = 0$$
其中 $\nabla_T^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$ 是横向拉普拉斯算子。所有的激光模式，都是这个方程在不同坐标系下的本征解。

第二章：基模高斯光束 ($TEM_{00}$)

在圆柱坐标系下求解上述方程，最简单的解就是基模高斯光束。它是激光器在理想状态下输出的模式。

2.1 完整的复振幅分布

$$E(r, z) = E_0 \frac{w_0}{w(z)} \exp \left( -\frac{r^2}{w(z)^2} \right) \exp \left( -i \left[ kz + \frac{k r^2}{2R(z)} - \zeta(z) \right] \right)$$

2.2 核心参数详解

这是工程师必须烂熟于心的四个公式：

  1. 束腰半径 (Beam Waist) $w_0$：
    光束最窄处的半径（强度降至 $1/e^2$）。它是光束的“源头”。

  2. 瑞利长度 (Rayleigh Range) $z_R$：
    $$z_R = \frac{\pi w_0^2}{\lambda}$$
    光束截面积增加一倍（半径增加 $\sqrt{2}$ 倍）的传播距离。$z_R$ 越大，光束准直性越好。

  3. 光斑半径演化 $w(z)$：
    $$w(z) = w_0 \sqrt{1 + \left( \frac{z}{z_R} \right)^2}$$
    在远场 ($z \gg z_R$)，光束呈线性发散，发散半角为 $\theta = \lambda / (\pi w_0)$。这揭示了衍射极限：束腰越细，发散越快。

  4. 波前曲率半径 $R(z)$：
    $$R(z) = z \left[ 1 + \left( \frac{z_R}{z} \right)^2 \right]$$

    • $z=0$ 时，$R \to \infty$（平面波）。
    • $z=z_R$ 时，$R$ 最小（波前最弯）。
    • $z \to \infty$ 时，$R \approx z$（球面波）。

  5. Gouy 相移 $\zeta(z)$：
    $$\zeta(z) = \arctan \left( \frac{z}{z_R} \right)$$
    这是因光束横向限制而产生的额外轴向相移。光束从 $-\infty$ 传到 $+\infty$，总共会比平面波多经历 $\pi$ 的相位差。这对于计算激光谐振腔的共振频率至关重要。

更多高斯光束核心参数介绍，可参考激光物理笔记：从波动方程到高斯光束 (Gaussian Beam) 的完整推导与核心指标

第三章：复光束参数 q 与 ABCD 定律

在实际光学设计（如扩束镜、聚焦透镜设计）中，我们不会直接代入上面的公式，而是使用更强大的工具：q 参数。

3.1 q 参数的定义

我们将光斑半径 $w(z)$ 和曲率半径 $R(z)$ 统一到一个复数参数 $q(z)$ 中：
$$\frac{1}{q(z)} = \frac{1}{R(z)} - i \frac{\lambda}{\pi w(z)^2}$$

这个定义的精妙之处在于，自由传播距离 $z$ 后，q 参数的变化极简单：
$$q(z) = q_{0} + z = i z_R + z$$

3.2 ABCD 传输矩阵

当高斯光束通过任何傍轴光学系统（透镜、反射镜、介质界面）时，其 q 参数服从莫比乌斯变换 (Möbius transformation)：

$$q_{out} = \frac{A q_{in} + B}{C q_{in} + D}$$

其中 $A, B, C, D$ 是射线光学中的传输矩阵元。

  • 应用举例：透镜聚焦。
    透镜矩阵为 $\begin{bmatrix} 1 & 0 \ -1/f & 1 \end{bmatrix}$。
    代入公式即可计算出聚焦后的新束腰位置和大小。这是 ZEMAX 等软件计算高斯光束传播的核心算法。

第四章：厄米-高斯模式 ($HG_{mn}$)

当激光谐振腔具有矩形对称性（例如腔内放置了布儒斯特窗，或者晶体是长方体），波动方程在笛卡尔坐标系 $(x,y,z)$ 下分离变量。

4.1 物理描述

解可以表示为 $u(x,y,z) = u_m(x,z) u_n(y,z)$。
复振幅表达式为：
$$E_{mn} = E_0 \frac{w_0}{w(z)} H_m \left( \frac{\sqrt{2}x}{w} \right) H_n \left( \frac{\sqrt{2}y}{w} \right) e^{-\frac{r^2}{w^2}} e^{-ikz - i\frac{kr^2}{2R} + i(m+n+1)\zeta(z)}$$

4.2 厄米多项式 $H_n$

光斑的形状由厄米多项式决定：

  • $n=0: H_0(x) = 1$ (高斯)
  • $n=1: H_1(x) = 2x$ (中心过零点，分为两瓣)
  • $n=2: H_2(x) = 4x^2 - 2$ (三瓣，旁瓣小，主瓣大)
  • $n=3: H_3(x) = 8x^3 - 12x$

4.3 物理意义

  • 简并破除：注意相位因子 $(m+n+1)\zeta(z)$。高阶模的 Gouy 相移更大。这意味着在同一个谐振腔中，不同横模的共振频率略有不同。
  • 正交性：不同阶数的 HG 模式在全空间内是正交的。这意味着如果不受微扰，它们之间不会发生能量耦合。

第五章：拉盖尔-高斯模式 ($LG_{pl}$)

当系统具有圆柱对称性（如光纤、完美圆形的透镜），我们在 $(r, \phi, z)$ 坐标系下求解。

5.1 轨道角动量 (OAM) 的引入

LG 模式最引人注目的特征是其螺旋相位项 $\exp(-il\phi)$。
$$E_{pl} \propto \left( \frac{r\sqrt{2}}{w} \right)^{|l|} L_p^{|l|} \left( \frac{2r^2}{w^2} \right) e^{-\frac{r^2}{w^2}} e^{-il\phi} e^{i(2p+|l|+1)\zeta(z)}$$

5.2 参数解读

  • $p$ (径向指数)：决定了沿半径方向的光环数量 ($p+1$ 个环)。
  • $l$ (拓扑荷数/角向指数)：
    • 决定了相位的螺旋速度。
    • 决定了中心的暗核大小（离心势垒）。
    • 每个光子携带 $l\hbar$ 的轨道角动量。

5.3 产生与应用

  • 产生：使用螺旋相位板 (Spiral Phase Plate) 或空间光调制器 (SLM) 将基模高斯光束转换为 LG 模式。
  • 应用：
    • STED 显微镜：利用甜甜圈光束擦除荧光，突破衍射极限。
    • 光通信：利用 $l$ 的无限正交性进行空分复用 (MDM/OAM Multiplexing)。

第六章：工程指标——光束质量 $M^2$

现实中的激光器输出的永远不是纯净的基模，而是多种模式的混合。工程师如何量化这束光“好不好用”？答案是 $M^2$ 因子。

6.1 定义

实际光束的束腰宽度 $W_{real}$ 和远场发散角 $\Theta_{real}$ 的乘积（光束参数积 BPP），与理想高斯光束的 BPP 之比：
$$M^2 = \frac{W_{real} \Theta_{real}}{w_0 \theta_0} \ge 1$$

6.2 物理含义

  • $M^2 = 1$：衍射极限，完美高斯光束。
  • $M^2 > 1$：光束质量变差。例如，$M^2 = 1.5$ 的光束，在同样的透镜聚焦下，焦点光斑面积是基模的 1.5 倍（或者直径是 $\sqrt{1.5}$ 倍）。

6.3 模式含量与 $M^2$

对于纯的高阶模，$M^2$ 会显著增大：

  • $TEM_{00} \to M^2 = 1$
  • $TEM_{01} \to M^2 = 3$
  • $TEM_{nm} \to M^2 \approx 2n+1$
    这就是为什么在激光切割、打标应用中，我们极力抑制高阶模，追求基模输出。

第七章：MATLAB 仿真实现

为了让这篇手册具有实战意义，附上通用的模式生成代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
function plot_laser_mode(type, m, n, w0, z)
    % PLOT_LASER_MODE 仿真并绘制激光横模光场分布
    %
    % 参数说明:
    %   type : 模式类型，可选 'TEM00', 'HG', 'LG'
    %   m    : 
    %          - 对于 'HG' 模式，代表 x 方向阶数 (m)
    %          - 对于 'LG' 模式，代表径向指数 (p)
    %          - 对于 'TEM00'，此参数被忽略（可填 0）
    %   n    : 
    %          - 对于 'HG' 模式，代表 y 方向阶数 (n)
    %          - 对于 'LG' 模式，代表角向指数/拓扑荷数 (l)
    %          - 对于 'TEM00'，此参数被忽略（可填 0）
    %   w0   : 束腰半径 (单位: 米)，例如 1e-3 (1mm)
    %   z    : 传播距离 (单位: 米)，例如 0.5 (50cm)
    %
    % ================= 参数调用案例 (Example Usage) =================
    % 1. 绘制基模高斯光束 (TEM00)
    %    plot_laser_mode('TEM00', 0, 0, 1e-3, 0.5);
    %
    % 2. 绘制厄米-高斯模式 (HG 1,0) -> 像两个并排的光斑
    %    plot_laser_mode('HG', 1, 0, 1e-3, 0.5);
    %
    % 3. 绘制“田”字形模式 (HG 1,1)
    %    plot_laser_mode('HG', 1, 1, 1e-3, 0.5);
    %
    % 4. 绘制甜甜圈光束 (LG p=0, l=1) -> 携带轨道角动量
    %    plot_laser_mode('LG', 0, 1, 1e-3, 0.5);
    %
    % 5. 绘制复杂多环 LG 模式 (LG p=2, l=3)
    %    plot_laser_mode('LG', 2, 3, 1e-3, 0.5);
    % ==============================================================

    % --- 1. 物理常数与参数初始化 ---
    lambda = 1064e-9;       % 波长 (1064nm)
    k = 2 * pi / lambda;    % 波数
    zR = pi * w0^2 / lambda; % 瑞利长度

    % 计算 z 处的高斯光束参数
    w_z = w0 * sqrt(1 + (z/zR)^2);      % 光斑半径
    R_z = z * (1 + (zR/z)^2);           % 曲率半径
    zeta = atan(z/zR);                  % Gouy 相移基量

    % --- 2. 建立空间网格 ---
    % 自动调整绘图范围，确保能包住高阶模
    % 高阶模比基模更宽，大致系数 sqrt(m+1) 或 sqrt(l+1)
    scale_factor = 1.5 * sqrt(max([m, n, 1]) + 1); 
    L = scale_factor * w_z; 
    N_points = 400;                     % 网格分辨率
    [X, Y] = meshgrid(linspace(-L, L, N_points));
    [PHI, R] = cart2pol(X, Y);

    % --- 3. 计算基模高斯因子 (公共部分) ---
    % 幅度项 * 相位曲率项 * 平面波相位
    G = (w0 / w_z) * exp(-R.^2 / w_z^2) .* exp(-1i * (k*z + k*R.^2 / (2*R_z)));

    % --- 4. 根据模式类型计算完整复振幅 E ---
    if strcmpi(type, 'TEM00')
        % === TEM00 基模 ===
        % Gouy 相移因子: exp(i * zeta)
        gouy_phase = exp(1i * zeta);
        E = G .* gouy_phase;
        title_str = 'TEM_{00} Mode';

    elseif strcmpi(type, 'HG')
        % === HG 厄米-高斯模式 ===
        % 厄米多项式需归一化变量 sqrt(2)x/w
        u_x = sqrt(2) * X / w_z;
        u_y = sqrt(2) * Y / w_z;
        
        % 计算 Hermite 多项式 (调用自定义或 MATLAB 内置 hermiteH)
        H_m = hermiteH_func(m, u_x);
        H_n = hermiteH_func(n, u_y);
        
        % Gouy 相移: (m + n + 1) * zeta
        gouy_phase = exp(1i * (m + n + 1) * zeta);
        
        E = G .* H_m .* H_n .* gouy_phase;
        title_str = sprintf('HG_{%d%d} Mode', m, n);

    elseif strcmpi(type, 'LG')
        % === LG 拉盖尔-高斯模式 ===
        p = m; l = n; % 映射参数名
        
        % 归一化半径变量 2r^2/w^2
        rho_sq = 2 * R.^2 / w_z^2;
        
        % 径向项 (sqrt(2)r/w)^|l|
        term_radial = (sqrt(2) * R / w_z).^abs(l);
        
        % 广义拉盖尔多项式 L_p^|l|
        L_pl = laguerreL_func(p, abs(l), rho_sq);
        
        % 螺旋相位项 exp(-i*l*phi)
        phase_spiral = exp(-1i * l * PHI);
        
        % Gouy 相移: (2p + |l| + 1) * zeta
        gouy_phase = exp(1i * (2*p + abs(l) + 1) * zeta);
        
        E = G .* term_radial .* L_pl .* phase_spiral .* gouy_phase;
        title_str = sprintf('LG_{p=%d}^{l=%d} Mode', p, l);
    else
        error('未知模式类型。请使用 ''TEM00'', ''HG'' 或 ''LG''。');
    end

    % --- 5. 绘图 ---
    figure('Color', 'w', 'Position', [100, 100, 1000, 400]);
    colormap('hot');

    % 强度图 (Intensity)
    subplot(1, 2, 1);
    imagesc(linspace(-L, L, N_points), linspace(-L, L, N_points), abs(E).^2);
    axis square; axis xy;
    colorbar;
    xlabel('x (m)'); ylabel('y (m)');
    title([title_str, ' - Intensity I(x,y)']);

    % 相位图 (Phase)
    subplot(1, 2, 2);
    % 这里的相位加了 pi 是为了视觉效果更好（可选）
    phase_plot = angle(E);
    imagesc(linspace(-L, L, N_points), linspace(-L, L, N_points), phase_plot);
    axis square; axis xy;
    colorbar;
    % 使用 hsv 或 jet 色图更能体现相位的循环特性
    colormap(gca, 'jet'); 
    xlabel('x (m)'); ylabel('y (m)');
    title([title_str, ' - Phase \phi(x,y)']);
    
    sgtitle(['Beam Parameters: w_0 = ' num2str(w0*1e3) 'mm, z = ' num2str(z) 'm']);
end

% --- 辅助函数：简易 Hermite 多项式 ---
function H = hermiteH_func(n, x)
    if n==0, H = ones(size(x));
    elseif n==1, H = 2*x;
    elseif n==2, H = 4*x.^2 - 2;
    elseif n==3, H = 8*x.^3 - 12*x;
    else
        % 递归计算高阶 (H_{n+1} = 2xH_n - 2nH_{n-1})
        H_nm1 = 2*x;    % H1
        H_nm2 = ones(size(x)); % H0
        for k = 2:n
            H = 2*x.*H_nm1 - 2*(k-1)*H_nm2;
            H_nm2 = H_nm1;
            H_nm1 = H;
        end
    end
end

% --- 辅助函数：简易广义 Laguerre 多项式 ---
function L = laguerreL_func(p, l, x)
    if p==0
        L = ones(size(x));
    elseif p==1
        L = 1 + l - x;
    elseif p==2
        L = 0.5 * ( (l+1)*(l+2) - 2*(l+2)*x + x.^2 );
    else
        % 如需更高阶，建议调用 MATLAB Symbolic Toolbox 的 laguerreL
        % 这里仅提供 p=0,1,2 的解析式以减少对工具箱的依赖
        error('本简易代码仅支持 p <= 2，请使用 MATLAB 工具箱函数 laguerreL');
    end
end

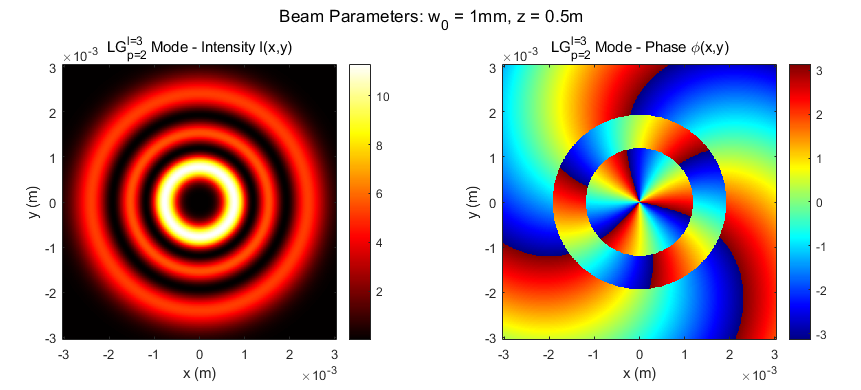
比如，运行第五个案例，“5. 绘制复杂多环 LG 模式 (LG p=2, l=3) plot_laser_mode(‘LG’, 2, 3, 1e-3, 0.5);”，