激光物理笔记:从波动方程到高斯光束 (Gaussian Beam) 的完整推导与核心指标
在几何光学中,我们习惯把光看作一条条直线(光线)。但在激光领域,光不再是直线,也不是理想的平面波,而是一种能量集中在轴心、沿横向呈高斯分布的高斯光束 (Gaussian Beam)。
它是激光器谐振腔输出的最基本模式 (TEM00)。要理解激光的聚焦、准直和传播特性,必须从它的数学本源——傍轴波动方程说起。
01. 物理起点:亥姆霍兹方程
回顾上一篇,单色光在真空中满足标量亥姆霍兹方程 (Helmholtz Equation):
$$
\nabla^2 E + k^2 E = 0
$$
其中 $k = 2\pi/\lambda$ 是波数。
设解 (Ansatz)
我们假设光束沿 $z$ 轴传播。如果是理想平面波,解是 $e^{-ikz}$。
但激光束在横截面 $(x, y)$ 上有强度分布,且随着传播距离 $z$ 会发生衍射(变宽)。
因此,我们假设解的形式为:
$$
E(x, y, z) = \psi(x, y, z) \cdot e^{-ikz}
$$
- $\psi(x, y, z)$ 是一个复振幅包络 (Complex Envelope),它包含了光束的横向分布和纵向的缓慢变化。
- $e^{-ikz}$ 是快速震荡的载波项。
02. 核心近似:缓变包络 (SVEA)
将上述设解代入亥姆霍兹方程。
首先算 $\nabla^2 E$。
对 $z$ 求导时,根据乘积法则:
$$
\frac{\partial E}{\partial z} = \left( \frac{\partial \psi}{\partial z} - ik\psi \right) e^{-ikz}
$$
$$
\frac{\partial^2 E}{\partial z^2} = \left( \frac{\partial^2 \psi}{\partial z^2} - 2ik\frac{\partial \psi}{\partial z} - k^2\psi \right) e^{-ikz}
$$
将 $\nabla^2 = \nabla_T^2 + \partial^2/\partial z^2$ (其中 $\nabla_T^2 = \partial^2/\partial x^2 + \partial^2/\partial y^2$)代回原方程,消去 $e^{-ikz}$ 和 $-k^2\psi$ 项,得到:
$$
\nabla_T^2 \psi - 2ik \frac{\partial \psi}{\partial z} + \frac{\partial^2 \psi}{\partial z^2} = 0
$$
引入傍轴近似 (Paraxial Approximation)
这是推导中最关键的一步。
激光束的特点是:它很直,发散很慢。这意味着包络 $\psi$ 随 $z$ 的变化(衍射效应)远慢于光波的震荡(波长尺度)。
数学上,这被称为缓变包络近似 (Slowly Varying Envelope Approximation, SVEA):
$$
\left| \frac{\partial^2 \psi}{\partial z^2} \right| \ll \left| 2k \frac{\partial \psi}{\partial z} \right|
$$
于是,二阶导数项 $\frac{\partial^2 \psi}{\partial z^2}$ 被忽略。我们得到了傍轴波动方程:
$$
\nabla_T^2 \psi - 2ik \frac{\partial \psi}{\partial z} = 0
$$
这个方程在数学上类似于薛定谔方程或热传导方程。
03. 高斯解的诞生
如果不去深究偏微分方程的分离变量解法,我们直接给出上述方程的一个基模解(TEM00):
$$
E(r, z) = E_0 \frac{w_0}{w(z)} \exp\left( \frac{-r^2}{w^2(z)} \right) \exp\left( -ikz - ik\frac{r^2}{2R(z)} + i\zeta(z) \right)
$$
这个看着很吓人的公式,其实可以拆解为三部分:
- 振幅项 $\frac{w_0}{w(z)} \exp(\frac{-r^2}{w^2(z)})$:描述光斑随距离变大,中心强度变弱,横向呈高斯分布。
- 相位弯曲项 $\exp(-ik\frac{r^2}{2R(z)})$:描述波前不是平面的,而是弯曲的球面波。
- 古伊相移项 $\exp(i\zeta(z))$:描述高斯光束特有的相位超前。
04. 工程师必须掌握的关键指标
做激光加工、光路耦合或 Zemax 模拟,你真正需要熟记的是下面这些参数:
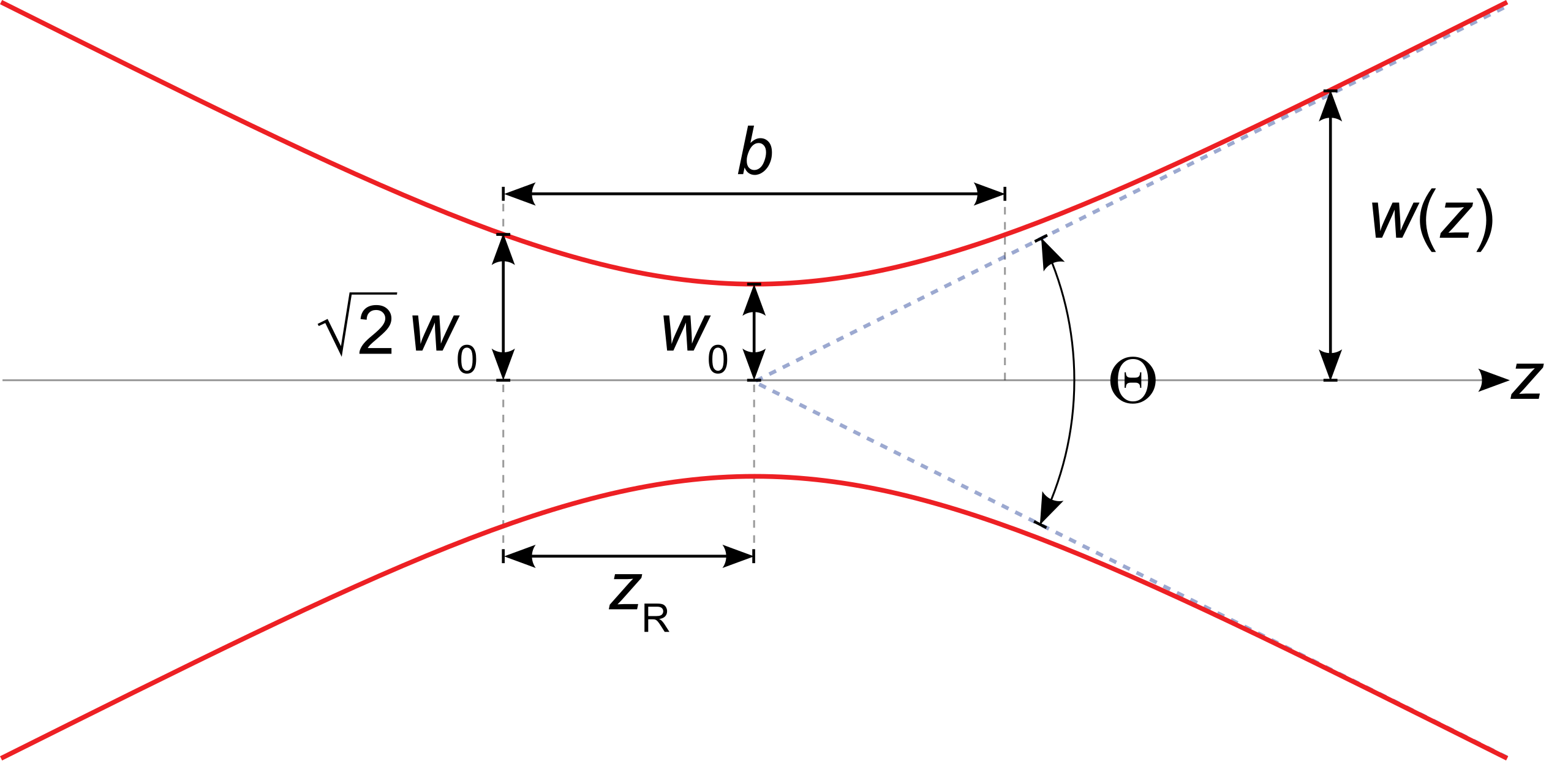
1. 束腰半径 (Beam Waist, $w_0$)
这是光束汇聚得最细的地方($z=0$ 处)。
- 物理意义:光束的“喉咙”。
- 能量定义:在 $r=w_0$ 处,光强下降到中心峰值的 $1/e^2$ (约 13.5%)。
2. 瑞利长度 (Rayleigh Range, $z_R$)
$$
z_R = \frac{\pi w_0^2}{\lambda}
$$
- 物理意义:光束保持“准直”的距离。
- 在 $z = z_R$ 处,光斑面积变为束腰处的 2 倍,光斑半径变为 $\sqrt{2}w_0$。
- 应用:在激光切割中,$2z_R$ 就是有效的景深(DOF)。$w_0$ 越小(聚得越细),$z_R$ 就越短(景深越浅),这是一个物理权衡。
3. 光斑随距离的变化 $w(z)$
$$
w(z) = w_0 \sqrt{1 + \left( \frac{z}{z_R} \right)^2}
$$
- 这是一个双曲线方程。
- 近场 ($z \ll z_R$):光束几乎是平行的。
- 远场 ($z \gg z_R$):光束呈线性发散。
4. 远场发散角 (Divergence Angle, $\theta$)
当 $z \to \infty$ 时,双曲线的渐近线夹角:
$$
\theta \approx \frac{\lambda}{\pi w_0}
$$
- 核心结论:束腰越细,发散角越大!
- 你不可能同时拥有极细的焦点和极远的发散距离(这受制于海森堡测不准原理在光学中的体现)。要让激光传得远($\theta$ 小),发射处的束腰 $w_0$ 必须做得很大(扩束器原理)。
5. 波前曲率半径 $R(z)$
$$
R(z) = z \left[ 1 + \left( \frac{z_R}{z} \right)^2 \right]
$$
- 在束腰处 ($z=0$),$R \to \infty$,是平面波。
- 在远场 ($z \to \infty$),$R \approx z$,是球面波。
- 这解释了为什么激光在焦点附近可以看作平面波,而传远了就变成了点光源发出的球面波。
05. 现实与理想:$M^2$ 因子
上述公式描述的是理想的高斯光束。但现实中的激光器输出总是不完美的。
我们引入 $M^2$ 因子 (Beam Quality Factor):
$$
\theta_{real} = M^2 \frac{\lambda}{\pi w_{0,real}}
$$
- 理想高斯光束:$M^2 = 1$。
- 实际激光束:$M^2 > 1$。
- $M^2$ 越大,光束质量越差,聚焦后的光斑越大,能量密度越低。
总结
高斯光束是波动方程在傍轴近似下的完美数学解。作为光学工程师,当你拿起透镜聚焦激光时,脑海里应该浮现出那条优雅的双曲线:
- $w_0$ 决定了你能刻多细的线。
- $z_R$ 决定了你能切多厚的板。
- $\theta$ 决定了你能照多远的距离。
它们通过波长 $\lambda$ 紧紧耦合在一起,无法打破,只能权衡。